Industrial production trends

This category group contains real-time measures of industrial production growth trends. These are based on individual countries’ most watched production volume indices and use both actual and estimated vintages of these indices, depending on availability. Growth trends are filtered changes of seasonally and calendar-adjusted vintages, whereby adjustment is based on only past observations.

Adjusted short-term industrial production trends

Ticker : IP_SA_P3M3ML3AR / _P6M6ML6AR / _4MMM_P1M1ML4AR

Label : Industrial production, seasonally and calendar adjusted: % 3m/3m ar / % 6m/6m ar / % 4mm/4mm ar

Definition : Industrial production index, adjusted for seasonal effects, working days and holidiays: % of latest 3 months over previous 3 months at an annualized rate / % of latest 6 months over previous 6 months at an annualized rate / % 4-month median over previous 4-month median at an annualized rate

Notes :

• Industrial production indices across countries use the most commonly watched local measures. In some countries, the index covers only manufacturing. In others, it is broader, including construction, mining and utilities.

• Seasonal adjustment factors are sequentially re-estimated as new data is released. Every re-estimation gives rise to a new data vintage that forms the basis of concurrent trend estimation.

• For most countries, calendar adjustment is applied, accounting for working day effects and moving holidays (e.g. Chinese New Year, Easter, Diwali, Ramadan etc).

• Switzerland, Australia and New Zealand only produce quarterly industrial production indices. For trend growth calculations, these indices are assumed to be stable over the quarter.

• China does not publish a production index. The official statistics only feature a % over a year ago series. This means that short-term industrial production trends cannot be calculated.

• The national sources series’ have been complemented by additional vintages provided by OECD’s ‘Revision Analysis Dataset’. See also Appendix 1 for details on OECD data integration.

Annual industrial production trends

Ticker : IP_SA_P1M1ML12_3MMA

Label : Industrial production: % oya, 3mma

Definition : Industrial production, seasonally and calendar adjusted: % over year ago, 3-month moving average.

Notes :

• See notes in the section on “Adjusted short-term industrial production trends”.

Imports

Only the standard Python data science packages and the specialized macrosynergy package are needed.

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math

import json
import yaml

import macrosynergy.management as msm
import macrosynergy.panel as msp
import macrosynergy.signal as mss
import macrosynergy.pnl as msn


from macrosynergy.download import JPMaQSDownload

from timeit import default_timer as timer
from datetime import timedelta, date, datetime

import warnings

warnings.simplefilter("ignore")

The JPMaQS indicators we consider are downloaded using the J.P. Morgan Dataquery API interface within the macrosynergy package. This is done by specifying ticker strings , formed by appending an indicator category code <category> to a currency area code <cross_section> . These constitute the main part of a full quantamental indicator ticker, taking the form DB(JPMAQS,<cross_section>_<category>,<info>) , where <info> denotes the time series of information for the given cross-section and category. The following types of information are available:

• value giving the latest available values for the indicator

• eop_lag referring to days elapsed since the end of the observation period

• mop_lag referring to the number of days elapsed since the mean observation period

• grade denoting a grade of the observation, giving a metric of real time information quality.

After instantiating the JPMaQSDownload class within the macrosynergy.download module, one can use the download(tickers,start_date,metrics) method to easily download the necessary data, where tickers is an array of ticker strings, start_date is the first collection date to be considered and metrics is an array comprising the times series information to be downloaded.

# Cross-sections of interest

cids_dmca = [
    "AUD",
    "CAD",
    "CHF",
    "EUR",
    "GBP",
    "JPY",
    "NOK",
    "NZD",
    "SEK",
    "USD",
]  # DM currency areas
cids_dmec = ["DEM", "ESP", "FRF", "ITL", "NLG"]  # DM euro area countries
cids_latm = ["BRL", "COP", "CLP", "MXN", "PEN"]  # Latam countries
cids_emea = ["CZK", "HUF", "ILS", "PLN", "RON", "RUB", "TRY", "ZAR"]  # EMEA countries
cids_emas = [
    "CNY",
    # "HKD",
    "IDR",
    "INR",
    "KRW",
    "MYR",
    "PHP",
    "SGD",
    "THB",
    "TWD",
]  # EM Asia countries

cids_dm = cids_dmca + cids_dmec
cids_em = cids_latm + cids_emea + cids_emas

cids = sorted(cids_dm + cids_em)

# Quantamental categories of interest

main = [
    "IP_SA_P3M3ML3AR",
    "IP_SA_P6M6ML6AR",
    "IP_SA_P1M1ML12_3MMA",
    "IP_SA_4MMM_P1M1ML4AR",
]
econ = ["RIR_NSA"]  # economic context
mark = [
    "FXXR_NSA",
    "FXXR_VT10",
    "DU05YXR_NSA",
    "DU05YXR_VT10",
    "FXUNTRADABLE_NSA",
    "FXTARGETED_NSA",
]  # market links

xcats = main + econ + mark

# Special industry-related commodity data set

cids_co = ["ALM", "CPR", "LED", "NIC", "TIN", "ZNC"]
xcats_co = ["COXR_VT10", "COXR_NSA"]
tix_co = [c + "_" + x for c in cids_co for x in xcats_co]

# Download series from J.P. Morgan DataQuery by tickers

start_date = "1990-01-01"
tickers = [cid + "_" + xcat for cid in cids for xcat in xcats] + tix_co
print(f"Maximum number of tickers is {len(tickers)}")

# Retrieve credentials

client_id: str = os.getenv("DQ_CLIENT_ID")
client_secret: str = os.getenv("DQ_CLIENT_SECRET")

# Download from DataQuery

with JPMaQSDownload(client_id=client_id, client_secret=client_secret) as downloader:
    start = timer()
    df = downloader.download(
        tickers=tickers,
        start_date=start_date,
        metrics=["value", "eop_lag", "mop_lag", "grading"],
        suppress_warning=True,
        show_progress=True,
    )
    end = timer()

dfd = df

print("Download time from DQ: " + str(timedelta(seconds=end - start)))

Maximum number of tickers is 419
Downloading data from JPMaQS.
Timestamp UTC:  2023-07-14 09:30:04
Connection successful!
Number of expressions requested: 1676

Requesting data: 100%|█████████████████████████████████████████████████████████████████| 84/84 [00:27<00:00,  3.07it/s]
Downloading data: 100%|████████████████████████████████████████████████████████████████| 84/84 [00:59<00:00,  1.42it/s]

Download time from DQ: 0:01:55.448886

Availability

cids_exp = sorted(list(set(cids) - set(cids_dmec)))  # cids expected in category panels
msm.missing_in_df(dfd, xcats=main, cids=cids_exp)

Missing xcats across df:  set()
Missing cids for IP_SA_4MMM_P1M1ML4AR:  {'CNY'}
Missing cids for IP_SA_P1M1ML12_3MMA:  set()
Missing cids for IP_SA_P3M3ML3AR:  {'CNY'}
Missing cids for IP_SA_P6M6ML6AR:  {'CNY'}

Most real-time quantamental indicators of industrial production trends are available from the early 1990s. Indeed, this is true for all developed markets and most emerging markets. Malaysia, the Phillipines and Thailand are notable late starters, with data only available post-2000.

For the explanation of currency symbols, which are related to currency areas or countries for which categories are available, please view Appendix 2 .

xcatx = main
cidx = cids_exp

dfx = msm.reduce_df(dfd, xcats=xcatx, cids=cidx)
dfs = msm.check_startyears(
    dfx,
)
msm.visual_paneldates(dfs, size=(18, 3))

print("Last updated:", date.today())

Last updated: 2023-07-14

xcatx = main
cidx = cids_exp

plot = msm.check_availability(
    dfd, xcats=xcatx, cids=cidx, start_size=(18, 3), start_years=False
)

Vintage grading is perfect for most developed markets and some emerging economies.

xcatx = main
cidx = cids_exp

plot = msp.heatmap_grades(
    dfd,
    xcats=xcatx,
    cids=cidx,
    size=(18, 3),
    title=f"Average vintage grades from {start_date} onwards",
)

cidx = cids_exp

for x in main:
    xcatx = [x]
    msp.view_ranges(
        dfd,
        xcats=xcatx,
        cids=cidx,
        val="eop_lag",
        title="End of observation period lags (ranges of time elapsed since end of observation period in days)",
        start=start_date,
        kind="box",
        size=(16, 4),
    )
    msp.view_ranges(
        dfd,
        xcats=xcatx,
        cids=cidx,
        val="mop_lag",
        title="Median of observation period lags (ranges of time elapsed since middle of observation period in days)",
        start=start_date,
        kind="box",
        size=(16, 4),
    )

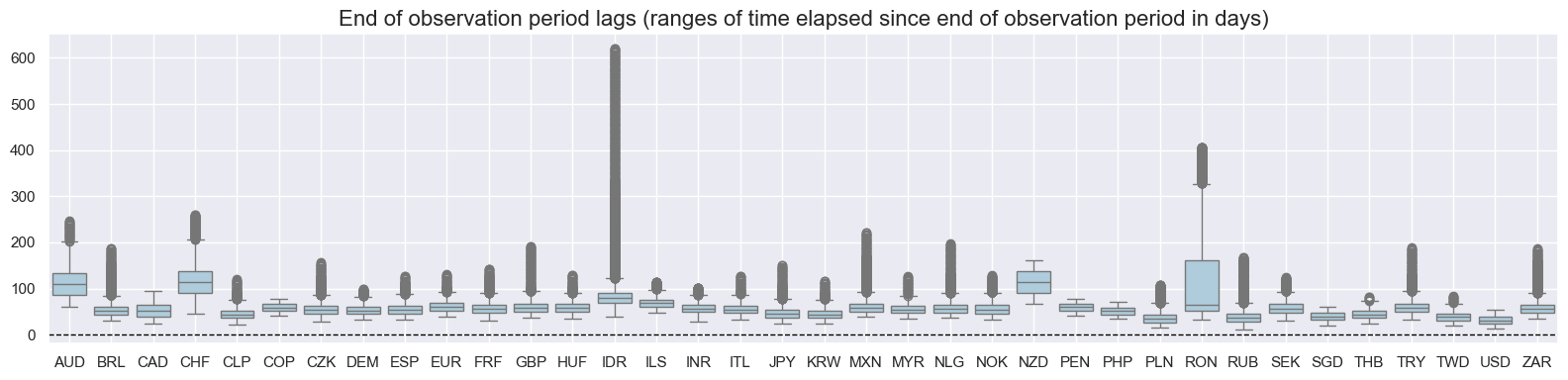
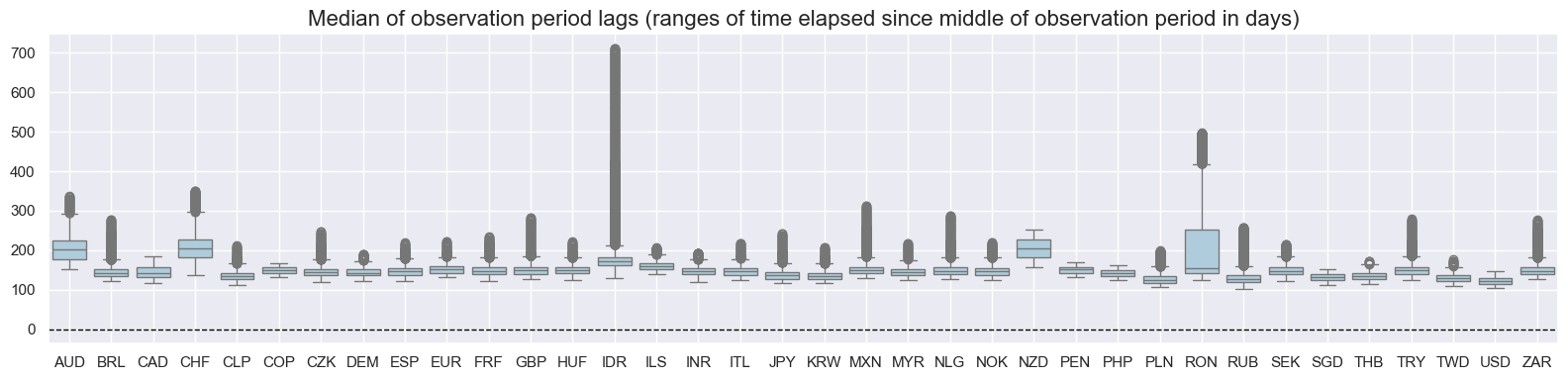
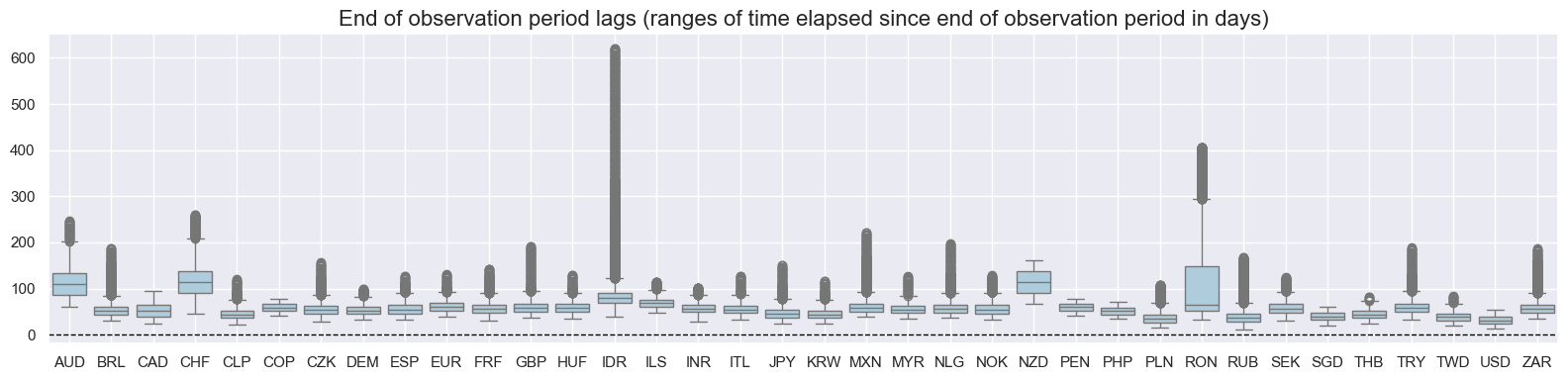
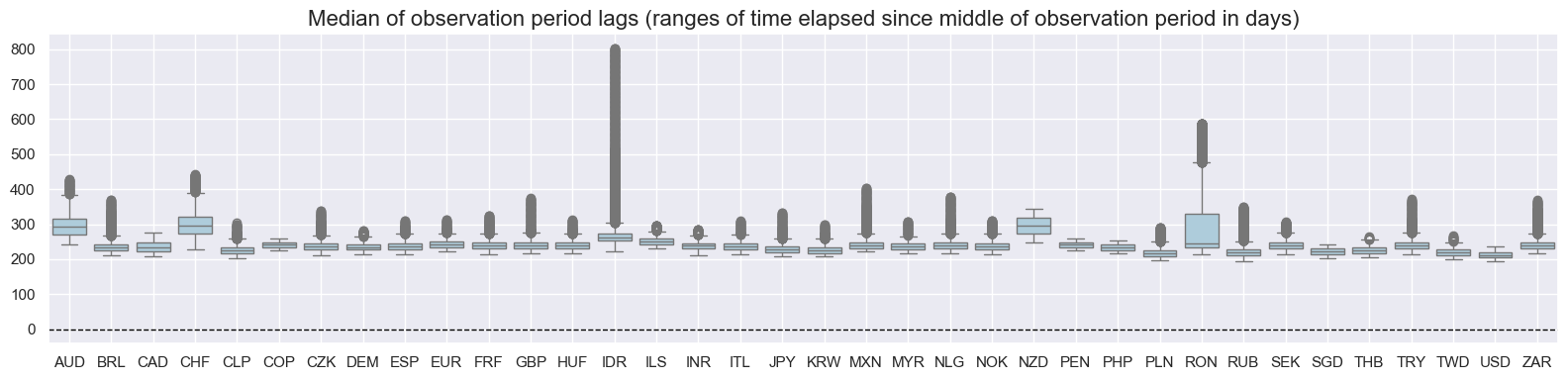
History

Industrial production trends

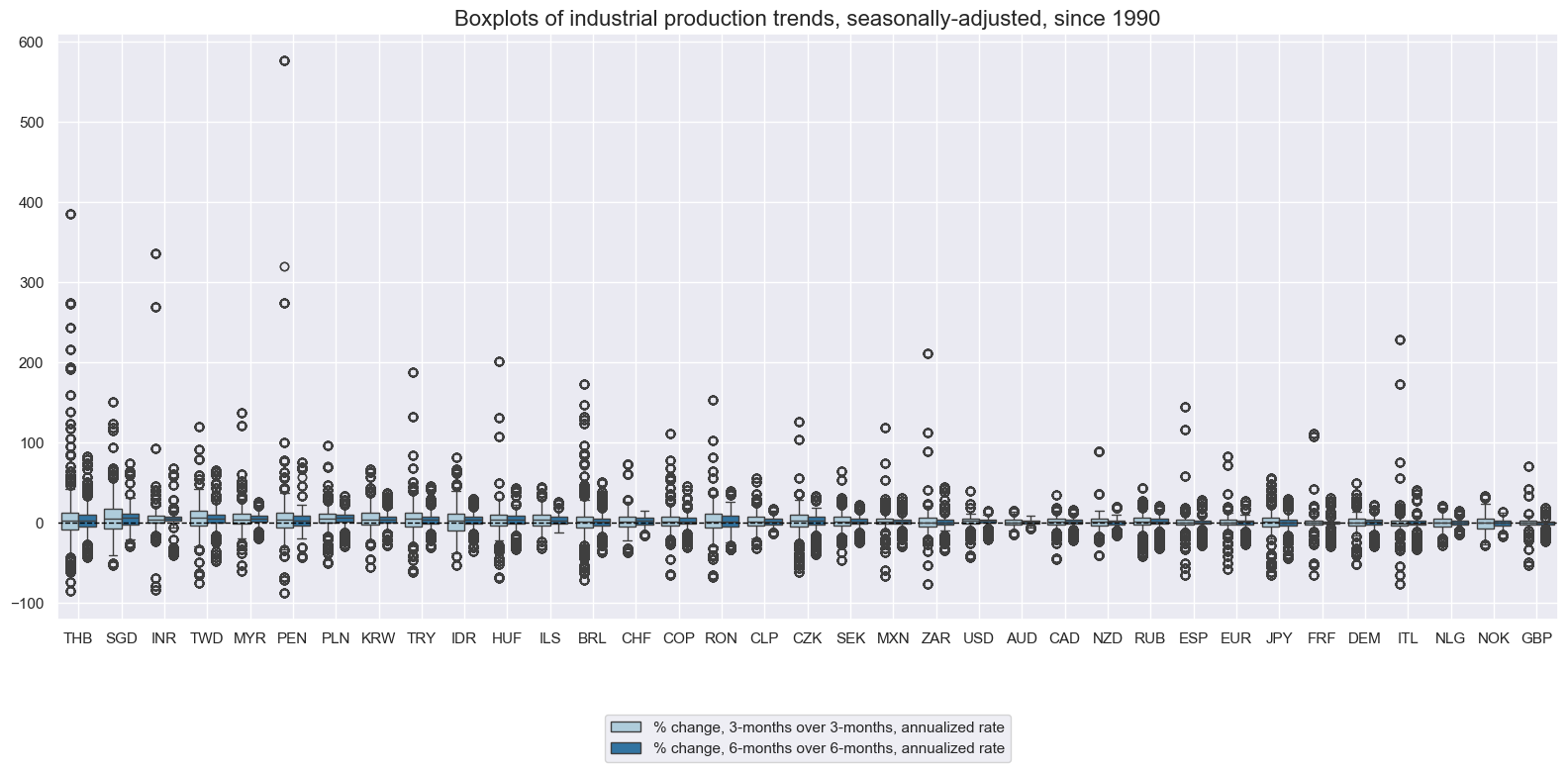
Short-term industrial production trends have often been indicative of cycles and mini-cycles in the manufacturing sector. The 6-month over 6-month changes have been substantially more stable than the 3-month over 3-month changes, even though the latter are more often used by financial economists. The 4-month median over 4-month median change is a good competitor for trends, but deals less well with the interpolated quarterly data. The 2020/21 Covid-19 pandemic has produced huge outliers in all metrics due to lockdowns and production shutdowns.

N.B.: The Philippines have been excluded from the below boxplot because during the COVID pandemic output essentially came to a halt and - due to subsequent base effects - recovery growth rates reached 17500%.

xcatx = ["IP_SA_P3M3ML3AR", "IP_SA_P6M6ML6AR"]
cidx = list(set(cids_exp) - set(["PHP"]))

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    sort_cids_by="mean",
    start=start_date,
    kind="box",
    title="Boxplots of industrial production trends, seasonally-adjusted, since 1990",
    xcat_labels=[
        "% change, 3-months over 3-months, annualized rate",
        "% change, 6-months over 6-months, annualized rate",
    ],
    size=(16, 8),
)

xcatx = ["IP_SA_P3M3ML3AR", "IP_SA_P6M6ML6AR"]
cidx = list(set(cids_exp) - set(["PHP"]))

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start=start_date,
    title="Industrial production trends, seasonally-adjusted, annualized rates",
    title_adj=1.02,
    title_xadj=0.435,
    title_fontsize=27,
    legend_fontsize=17,
    label_adj=0.075,
    xcat_labels=["3-month over 3-month", "6-month over 6-month"],
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=True,
)

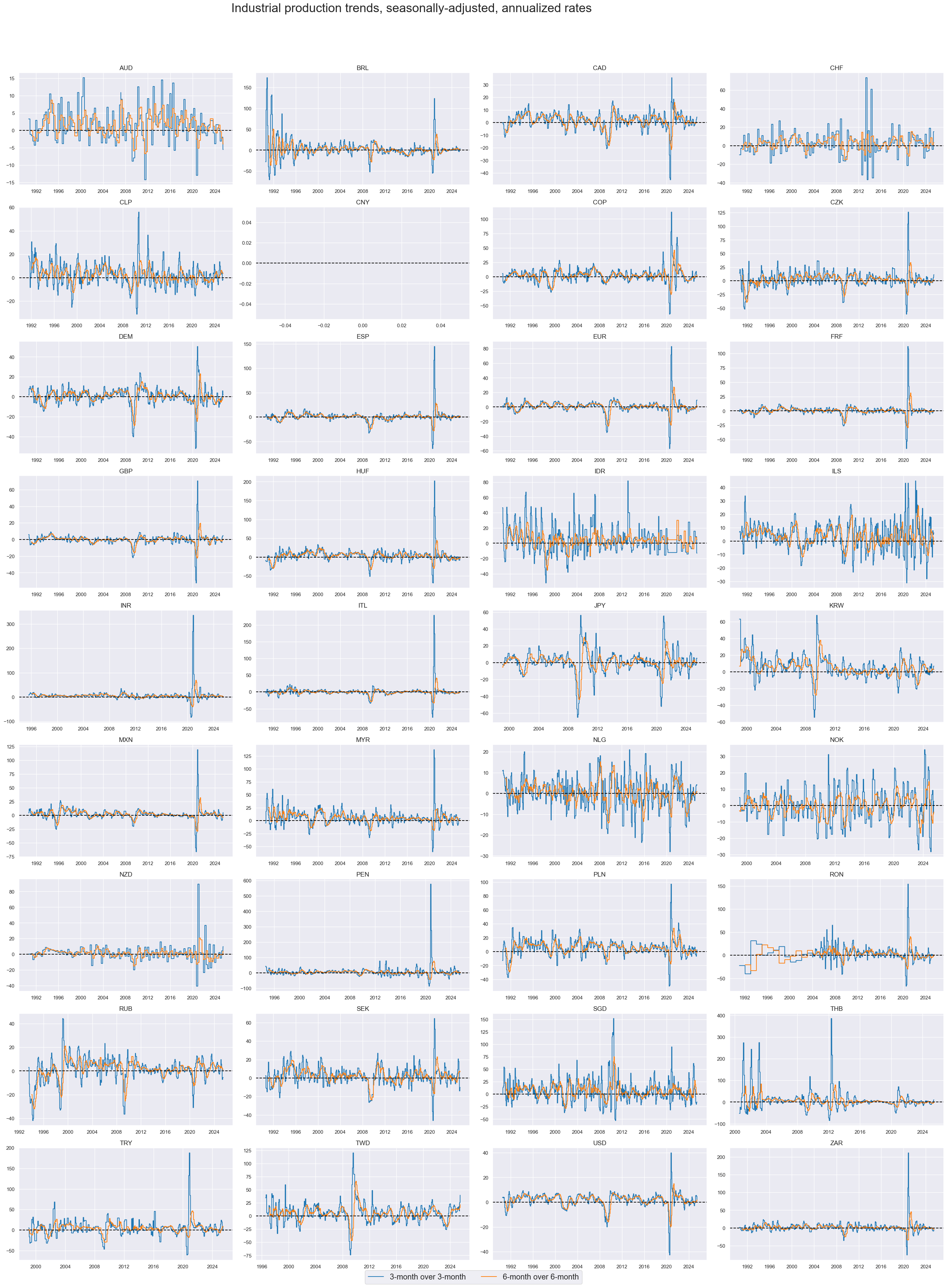
xcatx = ["IP_SA_4MMM_P1M1ML4AR", "IP_SA_P6M6ML6AR"]
cidx = list(set(cids_exp) - set(["PHP"]))

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start=start_date,
    title="Industrial production trends, seasonally-adjusted, annualized rates",
    title_adj=1.02,
    title_xadj=0.38,
    title_fontsize=27,
    legend_fontsize=17,
    xcat_labels=[
        "4-month moving median over 4-month moving median",
        "6-month over 6-month",
    ],
    label_adj=0.075,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
)

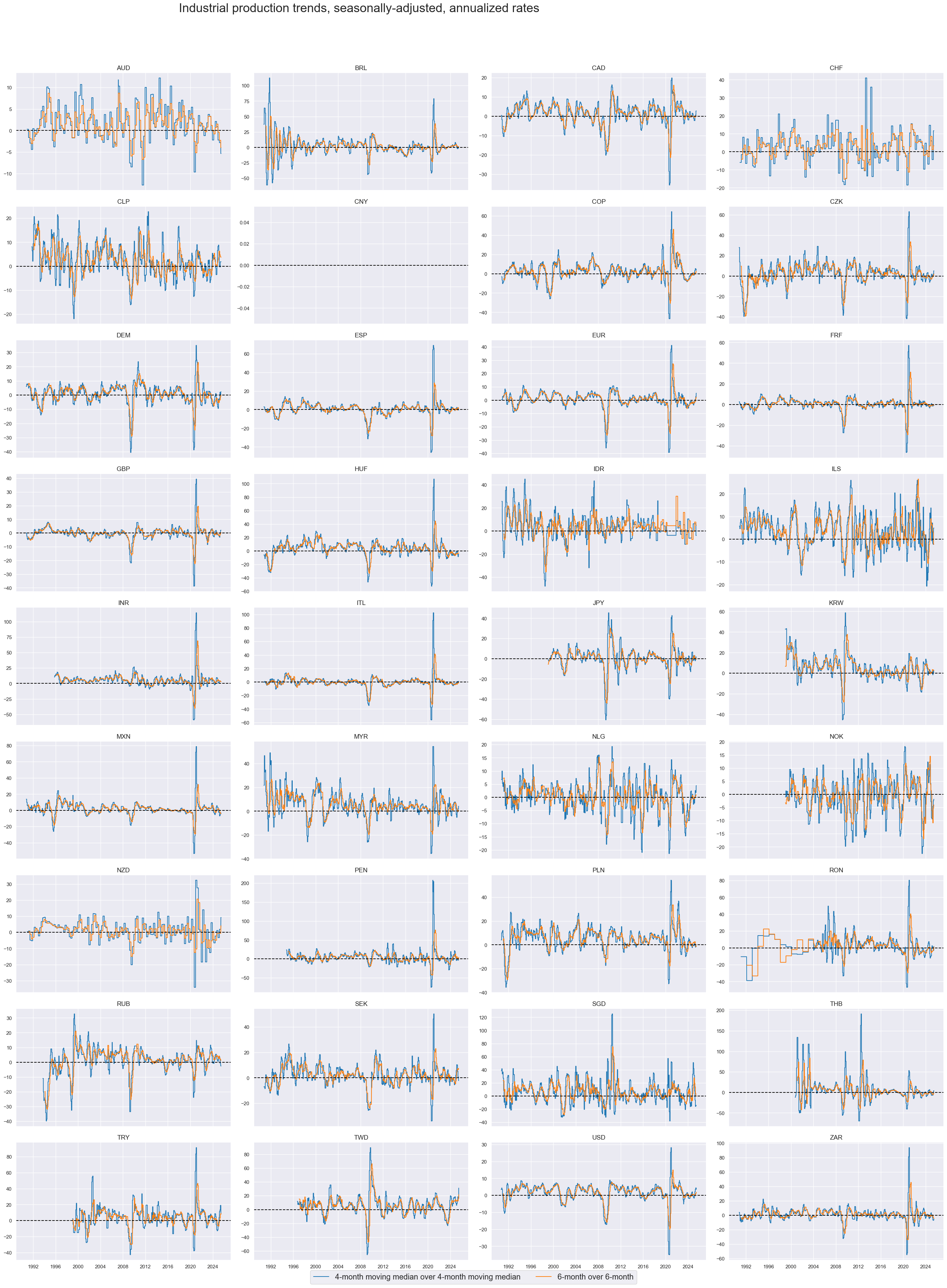
Due to a collapse on the production index in the wake of the first wave of the COVID pandemic, some subsequent annualized production trends in the Philippines posted unprecedented and unparalleled percent growth rates. For panel research it is typically advisable to trim or winsorize the series.

xcatx = ["IP_SA_4MMM_P1M1ML4AR", "IP_SA_P3M3ML3AR"]
cidx = "PHP"

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start=start_date,
    title=f"{cidx}: Industrial production trends, seasonally-adjusted, annualized rates",
    xcat_labels=[
        "4-month moving median over 4-month moving median",
        "3-month over 3-month",
    ],
    ncol=3,
    title_adj=1.05,
    same_y=False,
    size=(14, 7),
)

The quantamental indicators of 6-month production trends have been mostly positively correlated across almost all major economies, testifying to the impact of a global cycle.

xcatx = "IP_SA_P6M6ML6AR"
cidx = cids_exp

msp.correl_matrix(
    dfd,
    xcats=xcatx,
    cids=cidx,
    title="Cross-sectional correlations of 6-month industrial production trends, seasonally-adjusted, annualized rate, since 1990",
    size=(20, 14),
)

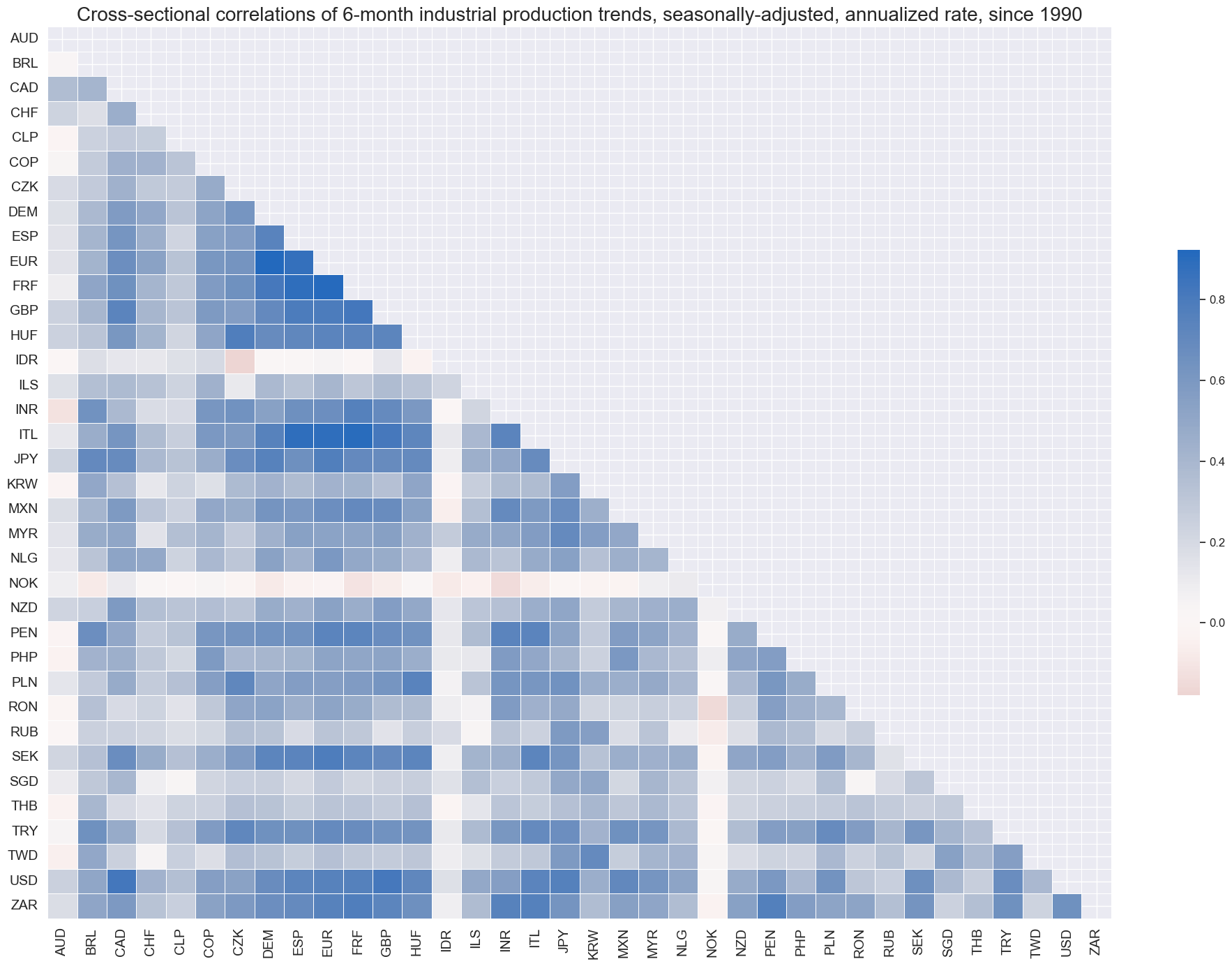
Annual industrial production trends

The average annual growth trend since 2000 has ranged from near zero in many developed countries to 10% in China. Intertemporal fluctuations have been larger than country differences and were mostly governed by a global cycle.

xcatx = ["IP_SA_P1M1ML12_3MMA"]
cidx = list(set(cids_exp) - set(["PHP"]))

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    sort_cids_by="mean",
    start=start_date,
    kind="box",
    title="Boxplots of annual industrial production trends, 3-month moving average, since 1990",
    xcat_labels=["% change over a year ago, 3-month moving average"],
    size=(16, 8),
)

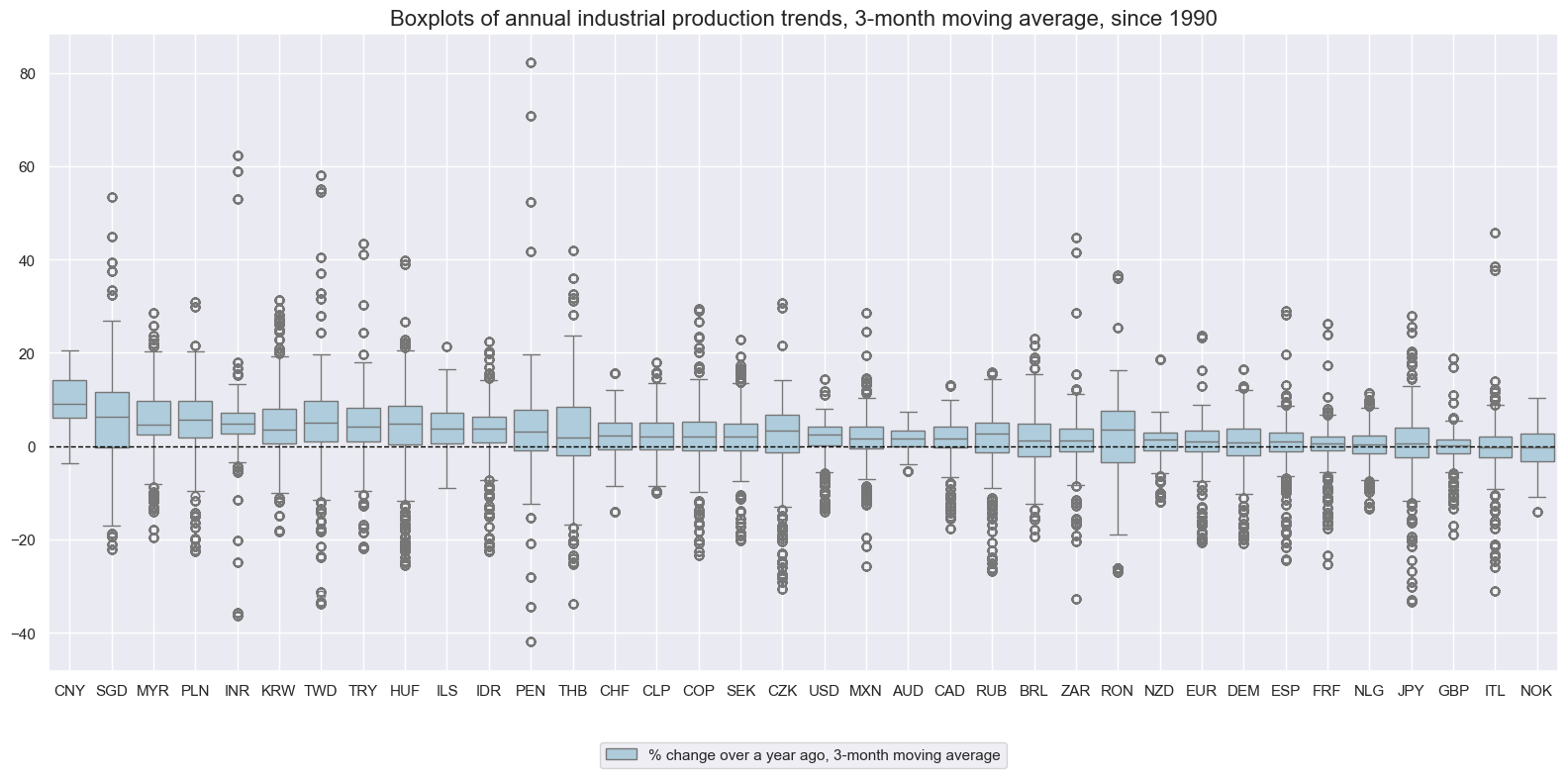
xcatx = ["IP_SA_P1M1ML12_3MMA"]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start=start_date,
    title="Industrial production, seasonally and calendar-adjusted, % over a year ago, 3-month moving average",
    title_adj=1.02,
    title_xadj=0.5,
    title_fontsize=27,
    legend_fontsize=17,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
)

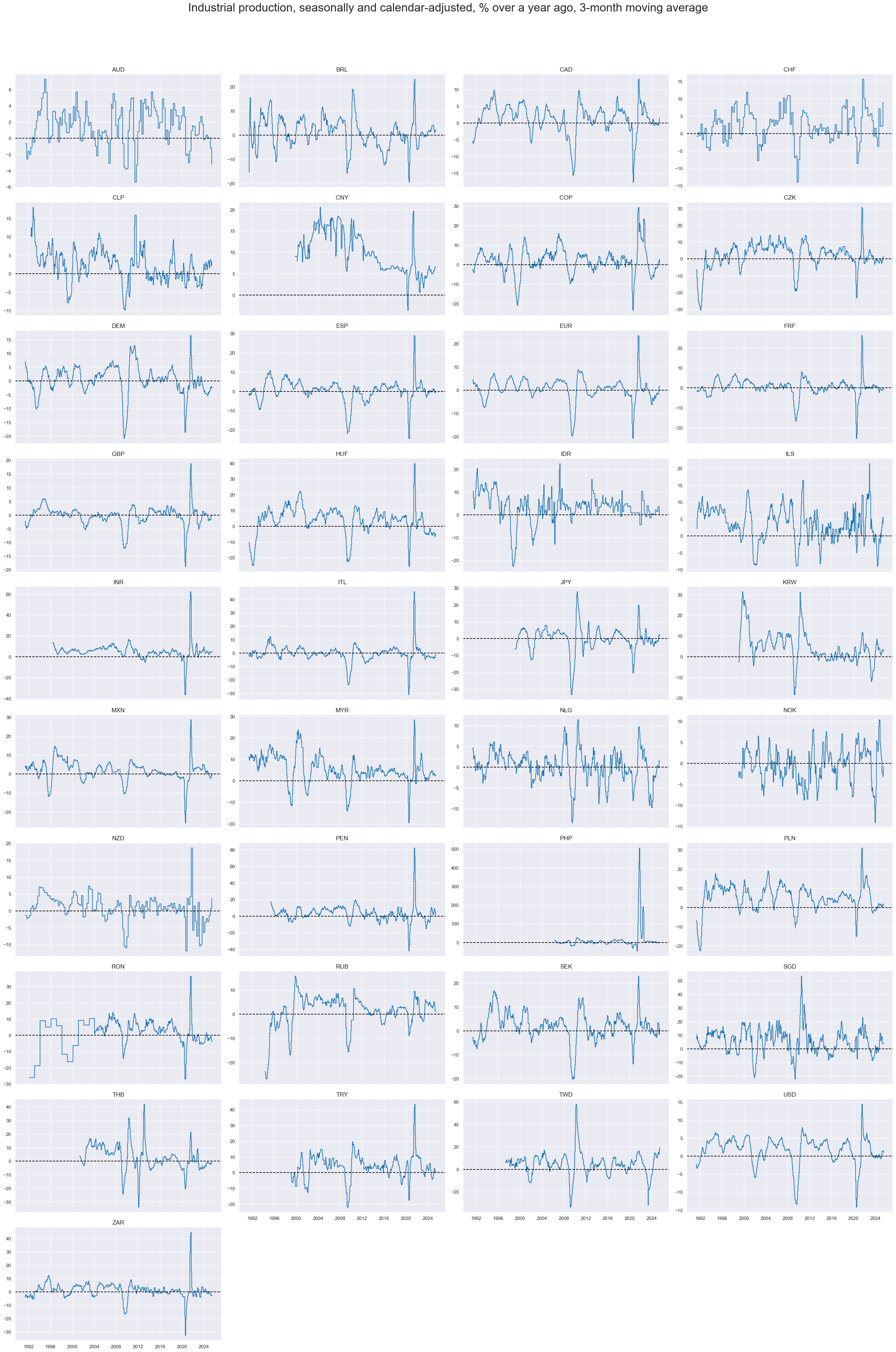
Annual growth trends are a good measure of the amplitude of industry cycles.

xcatx = ["IP_SA_P1M1ML12_3MMA"]
cidx = "EUR"

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start=start_date,
    title=f"{cidx}: Industrial production, % over a year ago, 3-month moving average",
    ncol=3,
    same_y=False,
    size=(14, 7),
)

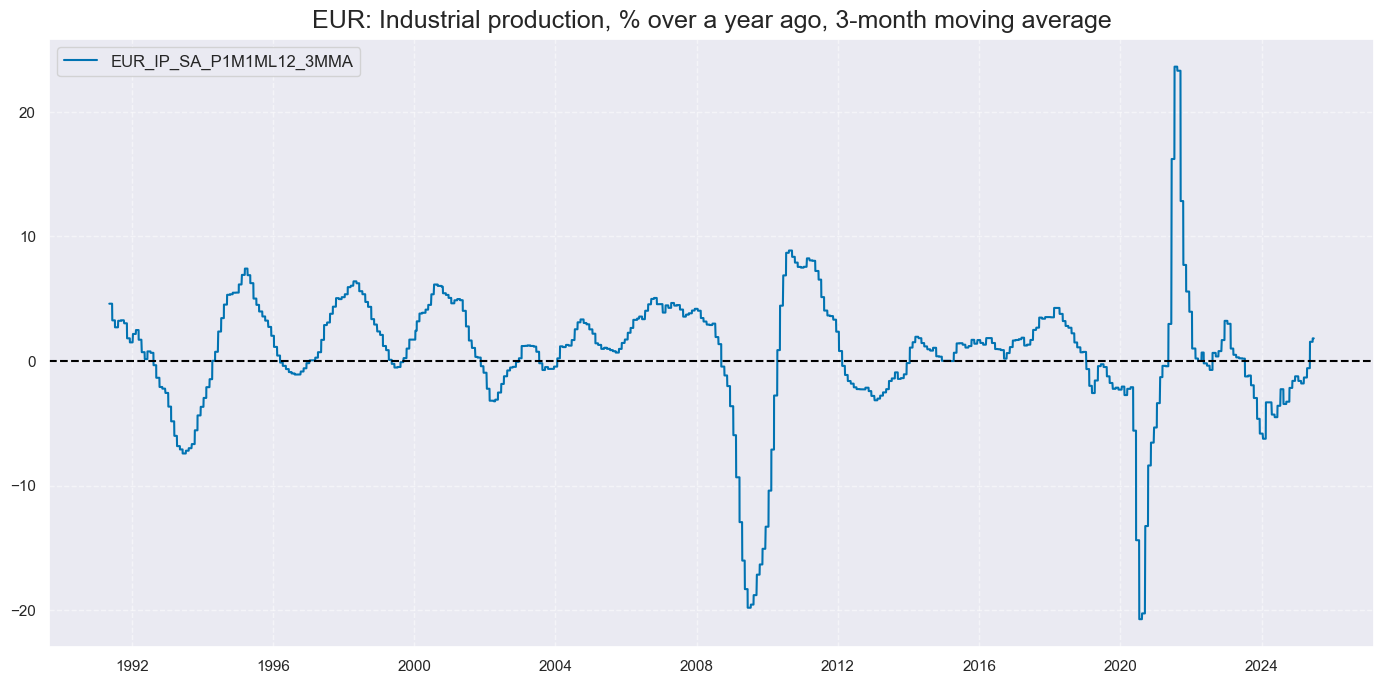
Importance

Research links

“Macroeconomic theory suggests that currencies of countries in a strong cyclical position should appreciate against those in a weak position. One metric for cyclical strength is the output gap, i.e. the production level relative to output at a sustainable operating rate.” Macrosynergy

Empirical clues

There is tentative evidence that the quantamental measures of medium-term differences in industry trends predict medium-term relative FX forward returns.

# Make blacklist dictionary for FX markets

dfb = df[df["xcat"].isin(["FXTARGETED_NSA", "FXUNTRADABLE_NSA"])].loc[
    :, ["cid", "xcat", "real_date", "value"]
]
dfba = (
    dfb.groupby(["cid", "real_date"])
    .aggregate(value=pd.NamedAgg(column="value", aggfunc="max"))
    .reset_index()
)
dfba["xcat"] = "FXBLACK"
fxblack = msp.make_blacklist(dfba, "FXBLACK")

cids_ip = dfd[dfd["xcat"] == "IP_SA_P3M3ML3AR"]["cid"].unique()
cids_fx = dfd[dfd["xcat"] == "FXXR_VT10"]["cid"].unique()
cids_ipfx = list(set(cids_ip).intersection(set(cids_fx)))

dfa = msp.make_relative_value(
    dfd,
    xcats=["IP_SA_P3M3ML3AR", "IP_SA_P6M6ML6AR", "IP_SA_P1M1ML12_3MMA", "FXXR_VT10"],
    cids=cids_ipfx,
    blacklist=fxblack,
)
dfd = msm.update_df(dfd, dfa)

xcatx = ["IP_SA_P1M1ML12_3MMAR", "FXXR_VT10R"]
cidx = cids_ipfx

cr = msp.CategoryRelations(
    dfd,
    xcats=xcatx,
    cids=cids_ipfx,
    freq="Q",
    lag=1,
    xcat_aggs=["mean", "sum"],
    fwin=1,
    xcat_trims=[40, 30],
    start="2000-01-01",
)

cr.reg_scatter(
    title="Relative industrial production trend and subsequent relative FX forward returns",
    labels=False,
    xlab="Industrial production, %oya, 3-month average, versus global (EM/DM) basket",
    ylab="FX forward return, next quarter, versus global (EM/DM) basket",
    coef_box="upper right",
)

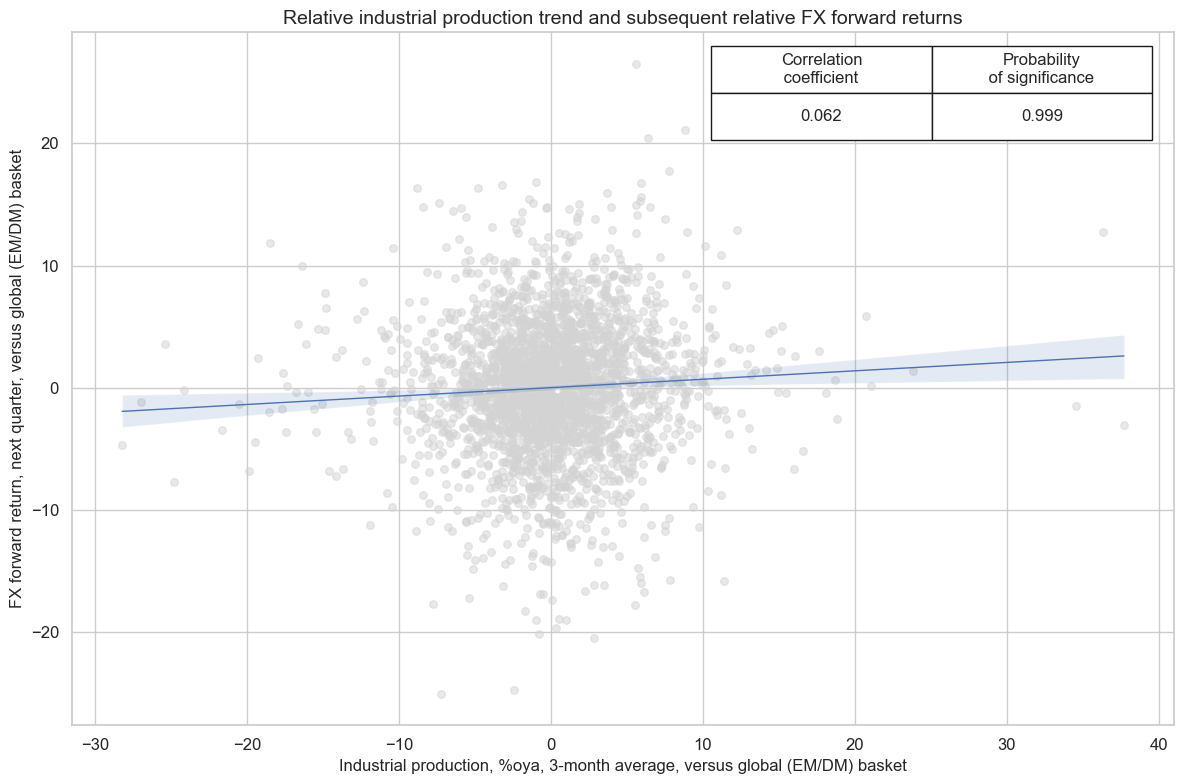
Global industrial production trends naturally affect demand and prices for industrial commodities concurrently, since producers are market participants. Since the data are backward looking they provide information on past economic effects on prices. And since unusually high or low production trends are typically not sustained but come in cycles they inform on temporary exaggerations and should plausibly be followed by paybacks.

This effect can be seen, for example, when looking at the relation between a G3 (U.S., euro area, Japan) industry trends and subsequent quarterly or even annual industrial metals (aluminum, copper, lead, nickel, tin and zinc) returns. The relation between yesterdays production and tomorrow’s return has been clearly negative, most conspicuously at the annual frequency.

cids_co = ["ALM", "CPR", "LED", "NIC", "TIN", "ZNC"]
cts = [cid + "_" for cid in cids_co]
bask_co = msp.Basket(dfd, contracts=cts, ret="COXR_VT10")
bask_co.make_basket(weight_meth="equal", basket_name="GLB")
dfa = bask_co.return_basket()

dfd = msm.update_df(dfd, dfa)  # Global industrial metals basket return

cids_ip = ["USD", "EUR", "JPY"]
cts = [cid + "_" for cid in cids_ip]
bask_co = msp.Basket(dfd, contracts=cts, ret="IP_SA_P1M1ML12_3MMA")
bask_co.make_basket(weight_meth="fixed", weights=[0.4, 0.4, 0.2], basket_name="GLB")
dfa = bask_co.return_basket()

dfd = msm.update_df(dfd, dfa)  # G3 IP growth basket

xcatx = ["IP_SA_P1M1ML12_3MMA", "COXR_VT10"]
cidx = ["GLB"]

cr = msp.CategoryRelations(
    dfd,
    xcats=xcatx,
    cids=cidx,
    freq="A",
    lag=1,
    xcat_aggs=["last", "sum"],
    fwin=1,
    xcat_trims=[40, 20],
    start="1992-01-01",
)

cr.reg_scatter(
    title="Industrial production trend and subsequent annual industrial metal returns since 1992",
    labels=False,
    xlab="G3 industrial production, %oya, 3-month average, end-of-year",
    ylab="Return of base metal futures basket, next year",
    coef_box="upper right",
)

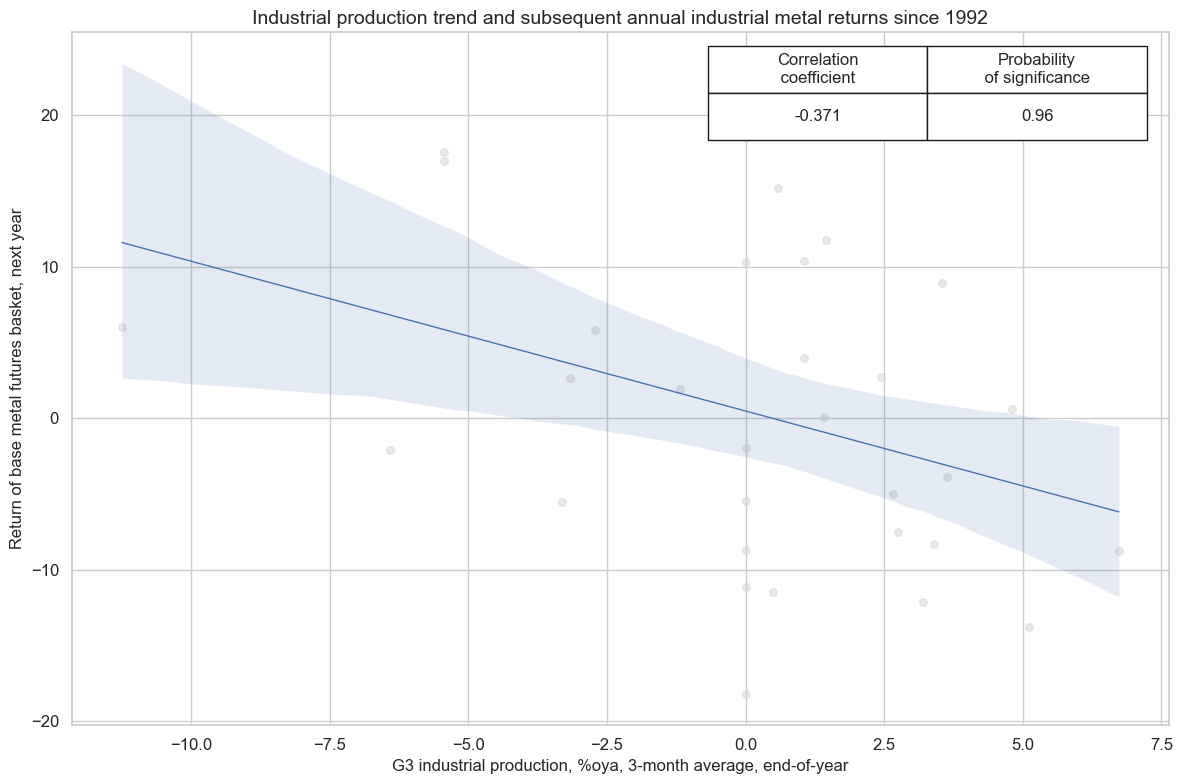
Appendices

Appendix 1: Notes on OECD data integration

Some indicators in this notebook are constructed using vintages provided by OECD’s ‘Revision Analysis Dataset’ in addition to national sources series’. The integration of the OECD datasets abide by the following rules:

1. The following priority order is applied for combining vintages. First, JPMaQS uses seasonally and calendar adjusted original vintages from national sources. Then, JPMaQS uses unadjusted original vintages from national sources. Beyond that, JPMaQS uses OECD vintages.

2. OECD vintages inform on the month of release but not the exact date. Actual release dates for these vintages are estimated based on release days of subsequent vintages.

3. Inconsistencies, data errors and missing values in the OECD vintages have been corrected for JPMaQS. This is particularly true for vintages that “lose” data that had been available in previous vintages (Switzerland and Russia).

Appendix 2: Currency symbols

The word ‘cross-section’ refers to currencies, currency areas or economic areas. In alphabetical order, these are AUD (Australian dollar), BRL (Brazilian real), CAD (Canadian dollar), CHF (Swiss franc), CLP (Chilean peso), CNY (Chinese yuan renminbi), COP (Colombian peso), CZK (Czech Republic koruna), DEM (German mark), ESP (Spanish peseta), EUR (Euro), FRF (French franc), GBP (British pound), HKD (Hong Kong dollar), HUF (Hungarian forint), IDR (Indonesian rupiah), ITL (Italian lira), JPY (Japanese yen), KRW (Korean won), MXN (Mexican peso), MYR (Malaysian ringgit), NLG (Dutch guilder), NOK (Norwegian krone), NZD (New Zealand dollar), PEN (Peruvian sol), PHP (Phillipine peso), PLN (Polish zloty), RON (Romanian leu), RUB (Russian ruble), SEK (Swedish krona), SGD (Singaporean dollar), THB (Thai baht), TRY (Turkish lira), TWD (Taiwanese dollar), USD (U.S. dollar), ZAR (South African rand).