Government bond returns #
This category group contains daily returns of zero-coupon generic government bonds or generic futures across major maturity tenors and countries.
Generic government bond returns #
Ticker : GB01YR_NSA / GB02YR_NSA / GB03YR_NSA / GB05YR_NSA / GB07YR_NSA / GB10YR_NSA / GB30YR_NSA
Label : Generic government bond returns: 1-year maturity / 2-year maturity / 3-year maturity / 5-year maturity / 7-year maturity / 10-year maturity / 30-year maturity.
Definition : Daily returns calculated from the continuous series of zero-coupon bond yields, daily roll: 1-year maturity / 2-year maturity / 3-year maturity / 5-year maturity / 7-year maturity / 10-year maturity / 30-year maturity.
Notes :
-
Total returns are calculated for generic zero-coupon bonds at different maturities based on zero coupon yield curves that are available on J.P. Morgan DataQuery. Excess returns – net of funding costs – and carry are calculated for these bonds based on related generic futures prices. The calculations are summarized in Appendix 1 .
-
Return calculation is based on daily rolling rebalancing, whereby each day we use the total return of the (constant maturity) government bond benchmark, adjusting for the 1-day roll.
Generic government bond excess returns #
Ticker : GB01YXR_NSA / GB02YXR_NSA / GB03YXR_NSA / GB05YXR_NSA / GB07YXR_NSA / GB10YXR_NSA / GB30YXR_NSA
Label : Generic government bond excess returns: 1-year maturity / 2-year maturity / 3-year maturity / 5-year maturity / 7-year maturity / 10-year maturity / 30-year maturity.
Definition : Daily excess returns calculated by adjusting the continuous series of zero-coupon bond yield returns for the Macrosynergy short-term interest rate indicator, daily roll: 1-year maturity / 2-year maturity / 3-year maturity / 5-year maturity / 7-year maturity / 10-year maturity / 30-year maturity.
Notes :
-
For most countries, a 1-month Libor rate has historically been used as a proxy for local funding costs. However, in the wake of the benchmark rate reform, this changed to other rates. For more information on the specific short term nominal interest rates used, please see here .
-
The risk-free rate is “de-annualized” by dividing by 252 business days, so that it is in line with our daily return calculation.
Vol-targeted generic government bond excess returns #
Ticker : GB01YXR_VT10 / GB02YXR_VT10 / GB03YXR_VT10 / GB05YXR_VT10 / GB07YXR_VT10 / GB10YXR_VT10 / GB30YXR_VT10
Label : Generic government bond excess returns for 10% vol target: 1-year maturity / 2-year maturity / 3-year maturity / 5-year maturity / 7-year maturity / 10-year maturity / 30-year maturity.
Definition : Daily excess returns scaled to 10% (annualized) volatility target, daily roll: 1-year maturity / 2-year maturity / 3-year maturity / 5-year maturity / 7-year maturity / 10-year maturity / 30-year maturity.
Notes :
-
Positions are scaled to a 10% volatility-target based on historic standard deviations for an exponential moving average of daily returns with an 11-day half-life of the lookback window. Positions are rebalanced at the end of each month and maximum leverage (notional to risk capital) is constrained to five.
Government bond future (excess) returns #
Ticker : GBF02YXR_NSA / GBF03YXR_NSA / GBF05YXR_NSA / GBF10YXR_NSA / GBF20YXR_NSA / GBF30YXR_NSA
Label : Government bond future returns: 2-year maturity / 3-year maturity / 5-year maturity / 10-year maturity / 20-year maturity / 30-year maturity.
Definition : Government bond front future returns: 2-year maturity / 3-year maturity / 5-year maturity / 10-year maturity / 20-year maturity / 30-year maturity.
Notes :
-
The return is simply the % change in the futures price. We construct a continuously rolling future series directly from the individual contracts that are a part of the regular trading cycle for that interest rate future. The return calculation assumes that the future position is rolled (from front to second) five business days before the expiry of the front contract. This is because rolls in the market on average happen one week before the last trading day.
-
Since futures are leverage-based instruments, these returns are excess returns.
Vol-targeted government bond future (excess) returns #
Ticker : GBF02YXR_VT10 / GBF03YXR_VT10 / GBF05YXR_VT10 / GBF10YXR_VT10 / GBF20YXR_VT10 / GBF30YXR_VT10
Label : Government bond future returns for 10% vol target: 2-year maturity / 3-year maturity / 5-year maturity / 10-year maturity / 20-year maturity / 30-year maturity.
Definition : Daily excess future returns scaled to 10% (annualized) volatility target, daily roll: 2-year maturity / 3-year maturity / 5-year maturity / 10-year maturity / 20-year maturity / 30-year maturity.
Notes :
-
Positions are scaled to 10% volatility target based on historic standard deviations for an exponential moving average of daily returns with an 11-day half-life of the lookback window. Positions are rebalanced at the end of each month and maximum leverage (notional to risk capital) is constrained to 5.
Imports #
Only the standard Python data science packages and the specialized
macrosynergy
package are needed.
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math
import json
import yaml
import macrosynergy.management as msm
import macrosynergy.panel as msp
import macrosynergy.signal as mss
import macrosynergy.pnl as msn
from macrosynergy.download import JPMaQSDownload
from timeit import default_timer as timer
from datetime import timedelta, date, datetime
import warnings
warnings.simplefilter("ignore")
The
JPMaQS
indicators we consider are downloaded using the J.P. Morgan Dataquery API interface within the
macrosynergy
package. This is done by specifying
ticker strings
, formed by appending an indicator category code
<category>
to a currency area code
<cross_section>
. These constitute the main part of a full quantamental indicator ticker, taking the form
DB(JPMAQS,<cross_section>_<category>,<info>)
, where
<info>
denotes the time series of information for the given cross-section and category. The following types of information are available:
-
valuegiving the latest available values for the indicator -
eop_lagreferring to days elapsed since the end of the observation period -
mop_lagreferring to the number of days elapsed since the mean observation period -
gradedenoting a grade of the observation, giving a metric of real time information quality.
After instantiating the
JPMaQSDownload
class within the
macrosynergy.download
module, one can use the
download(tickers,start_date,metrics)
method to easily download the necessary data, where
tickers
is an array of ticker strings,
start_date
is the first collection date to be considered and
metrics
is an array comprising the times series information to be downloaded.
cids = ["AUD", "DEM", "FRF", "ESP", "ITL", "JPY", "NZD", "GBP", "USD"]
rets = [
"GB01YR_NSA",
"GB02YR_NSA",
"GB03YR_NSA",
"GB05YR_NSA",
"GB07YR_NSA",
"GB10YR_NSA",
"GB30YR_NSA",
]
xrets = [
"GB01YXR_NSA",
"GB02YXR_NSA",
"GB03YXR_NSA",
"GB05YXR_NSA",
"GB07YXR_NSA",
"GB10YXR_NSA",
"GB30YXR_NSA",
]
xvolrets = [
"GB01YXR_VT10",
"GB02YXR_VT10",
"GB03YXR_VT10",
"GB05YXR_VT10",
"GB07YXR_VT10",
"GB10YXR_VT10",
"GB30YXR_VT10",
]
car = ["GB05YCRY_NSA", "GB05YCRY_VT10"]
futrets = [
"GBF02YXR_NSA",
"GBF03YXR_NSA",
"GBF05YXR_NSA",
"GBF10YXR_NSA",
"GBF20YXR_NSA",
"GBF30YXR_NSA",
]
futvolrets = [
"GBF02YXR_VT10",
"GBF03YXR_VT10",
"GBF05YXR_VT10",
"GBF10YXR_VT10",
"GBF20YXR_VT10",
"GBF30YXR_VT10",
]
xcats = rets + xrets + xvolrets + car + futrets + futvolrets
# Download series from J.P. Morgan DataQuery by tickers
start_date = "1990-01-01"
tickers = [cid + "_" + xcat for cid in cids for xcat in xcats]
print(f"Maximum number of tickers is {len(tickers)}")
# Retrieve credentials
client_id: str = os.getenv("DQ_CLIENT_ID")
client_secret: str = os.getenv("DQ_CLIENT_SECRET")
# Download from DataQuery
with JPMaQSDownload(client_id=client_id, client_secret=client_secret) as downloader:
start = timer()
assert downloader.check_connection()
df = downloader.download(
tickers=tickers,
start_date=start_date,
metrics=["value", "eop_lag", "mop_lag", "grading"],
suppress_warning=True,
show_progress=True,
)
end = timer()
dfd = df
print("Download time from DQ: " + str(timedelta(seconds=end - start)))
Maximum number of tickers is 315
Downloading data from JPMaQS.
Timestamp UTC: 2023-09-06 14:06:21
Connection successful!
Number of expressions requested: 1260
Requesting data: 100%|█████████████████████████████████████████████████████████████████| 63/63 [00:19<00:00, 3.21it/s]
Downloading data: 100%|████████████████████████████████████████████████████████████████| 63/63 [00:59<00:00, 1.05it/s]
Download time from DQ: 0:01:41.192367
Availability #
cids_exp = cids # cids expected in category panels
msm.missing_in_df(dfd, xcats=xcats, cids=cids_exp)
Missing xcats across df: []
Missing cids for GB01YR_NSA: []
Missing cids for GB01YXR_NSA: []
Missing cids for GB01YXR_VT10: []
Missing cids for GB02YR_NSA: []
Missing cids for GB02YXR_NSA: []
Missing cids for GB02YXR_VT10: []
Missing cids for GB03YR_NSA: []
Missing cids for GB03YXR_NSA: []
Missing cids for GB03YXR_VT10: []
Missing cids for GB05YCRY_NSA: []
Missing cids for GB05YCRY_VT10: []
Missing cids for GB05YR_NSA: []
Missing cids for GB05YXR_NSA: []
Missing cids for GB05YXR_VT10: []
Missing cids for GB07YR_NSA: []
Missing cids for GB07YXR_NSA: []
Missing cids for GB07YXR_VT10: []
Missing cids for GB10YR_NSA: []
Missing cids for GB10YXR_NSA: []
Missing cids for GB10YXR_VT10: []
Missing cids for GB30YR_NSA: []
Missing cids for GB30YXR_NSA: []
Missing cids for GB30YXR_VT10: []
Missing cids for GBF02YXR_NSA: ['JPY', 'FRF', 'AUD', 'NZD', 'ESP']
Missing cids for GBF02YXR_VT10: ['JPY', 'FRF', 'AUD', 'NZD', 'ESP']
Missing cids for GBF03YXR_NSA: ['JPY', 'ITL', 'GBP', 'FRF', 'DEM', 'USD', 'NZD', 'ESP']
Missing cids for GBF03YXR_VT10: ['JPY', 'ITL', 'GBP', 'FRF', 'DEM', 'USD', 'NZD', 'ESP']
Missing cids for GBF05YXR_NSA: ['JPY', 'ITL', 'FRF', 'NZD', 'ESP']
Missing cids for GBF05YXR_VT10: ['JPY', 'ITL', 'FRF', 'NZD', 'ESP']
Missing cids for GBF10YXR_NSA: ['NZD']
Missing cids for GBF10YXR_VT10: ['NZD']
Missing cids for GBF20YXR_NSA: ['ITL', 'GBP', 'FRF', 'DEM', 'USD', 'NZD', 'ESP']
Missing cids for GBF20YXR_VT10: ['ITL', 'GBP', 'FRF', 'DEM', 'USD', 'NZD', 'ESP']
Missing cids for GBF30YXR_NSA: ['JPY', 'ITL', 'FRF', 'AUD', 'NZD', 'ESP']
Missing cids for GBF30YXR_VT10: ['JPY', 'ITL', 'FRF', 'AUD', 'NZD', 'ESP']
For generic bonds, United States data are available from the early 1990s, but series for other bonds markets only start post-2000. Time series for Japan are only available from 2012 onwards.
For the explanation of currency symbols, which are related to currency areas or countries for which categories are available, please view Appendix 2 .
xcatx = [xc for xc in xcats if not xc.startswith("GBF")]
cidx = cids_exp
dfx = msm.reduce_df(dfd, xcats=xcatx, cids=cidx)
dfs = msm.check_startyears(
dfx,
)
msm.visual_paneldates(dfs, size=(14, 8))
print("Last updated:", date.today())
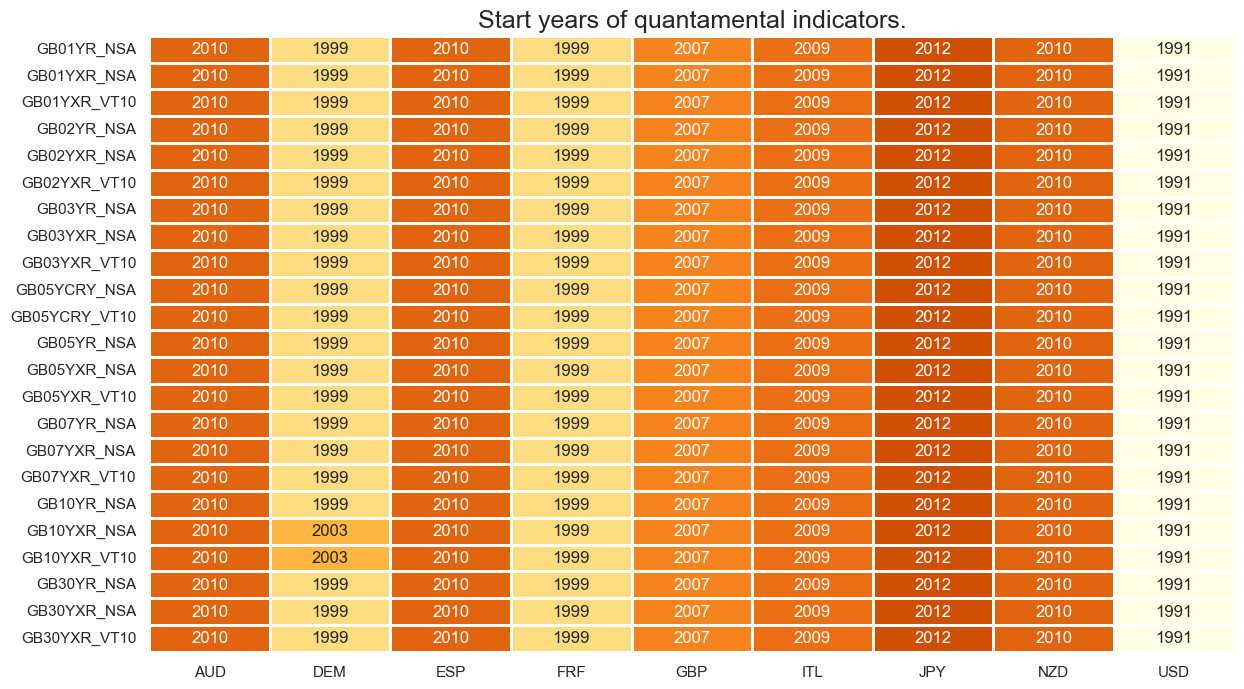
Last updated: 2023-09-06
xcatx = [xc for xc in xcats if not xc.startswith("GBF")]
cidx = cids_exp
plot = msm.check_availability(
dfd, xcats=xcatx, cids=cids_exp, start_size=(18, 6), start_years=False
)
Futures returns are available for much fewer market segments and with shorter history. The 10-year tenor is the only tenor for which all major developed bond markets have a history of futures returns.
xcatx = [xc for xc in xcats if xc.startswith("GBF")]
cidx = cids_exp
dfx = msm.reduce_df(dfd, xcats=xcatx, cids=cidx)
dfs = msm.check_startyears(
dfx,
)
msm.visual_paneldates(dfs, size=(14, 8))
print("Last updated:", date.today())
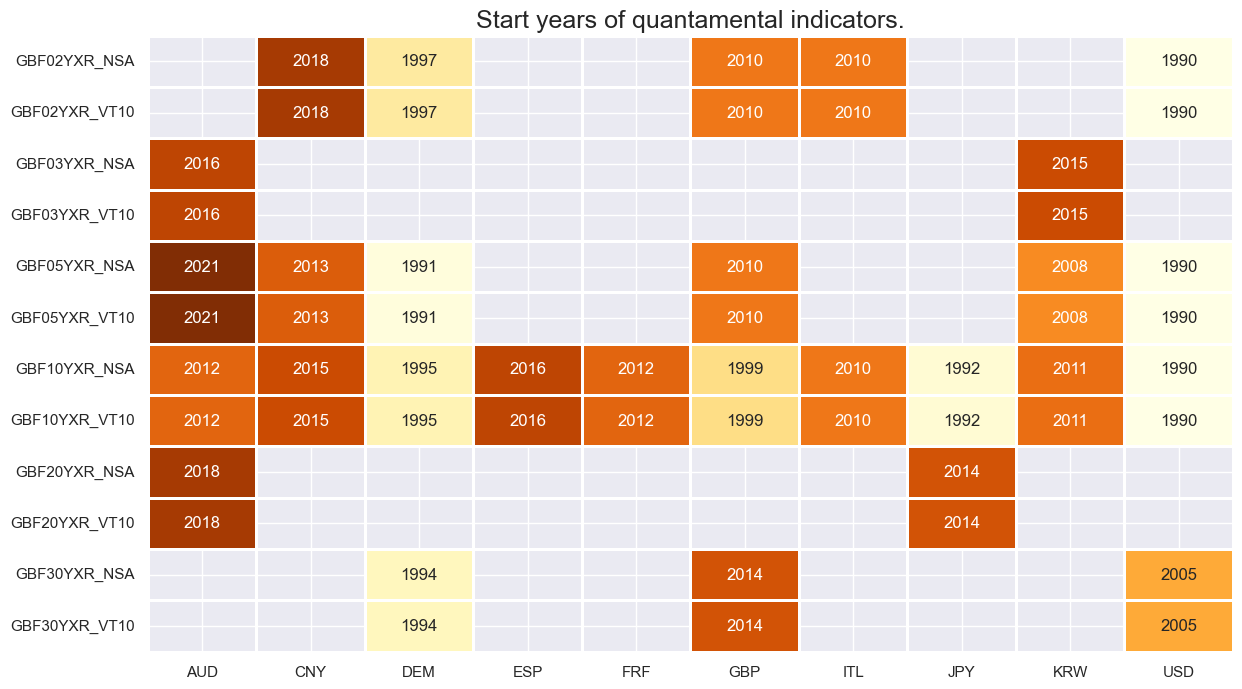
Last updated: 2023-09-06
xcatx = [xc for xc in xcats if xc.startswith("GBF")]
cidx = cids_exp
plot = msm.check_availability(
dfd, xcats=xcatx, cids=cids_exp, start_size=(18, 6), start_years=False
)
xcatx = xcats
cidx = cids_exp
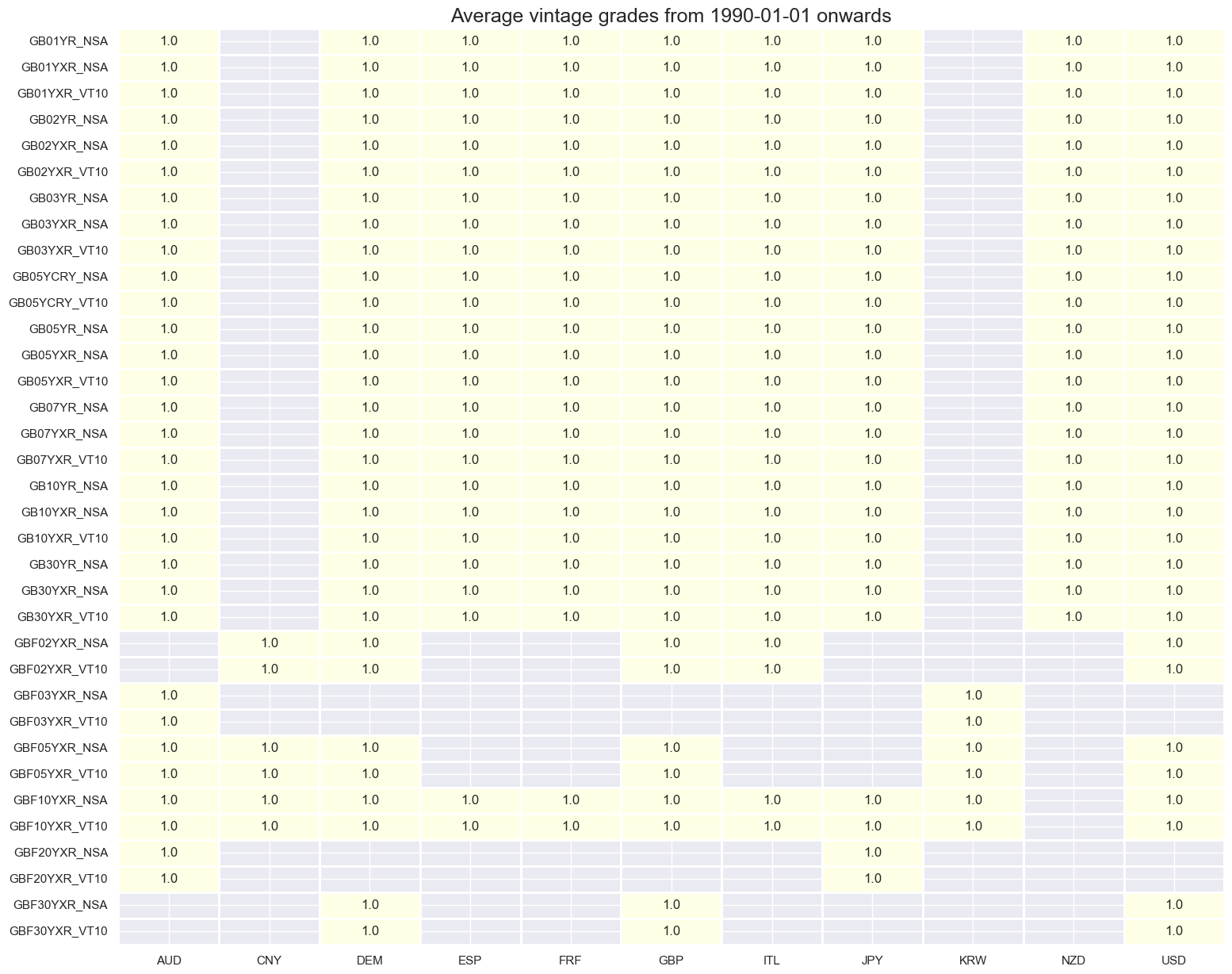
plot = msp.heatmap_grades(
dfd,
xcats=xcatx,
cids=cidx,
size=(18, 15),
title=f"Average vintage grades from {start_date} onwards",
)
xcatx = ["GB01YR_NSA", "GB05YR_NSA", "GB10YR_NSA"]
cidx = cids
msp.view_ranges(
dfd,
xcats=xcatx,
cids=cidx,
val="eop_lag",
title="End of observation period lags (ranges of time elapsed since end of observation period in days), government bond returns",
start=start_date,
kind="box",
size=(16, 4),
)
msp.view_ranges(
dfd,
xcats=xcatx,
cids=cidx,
val="mop_lag",
title="Median of observation period lags (ranges of time elapsed since middle of observation period in days), government bond returns",
start=start_date,
kind="box",
size=(16, 4),
)
History #
Government bond returns #
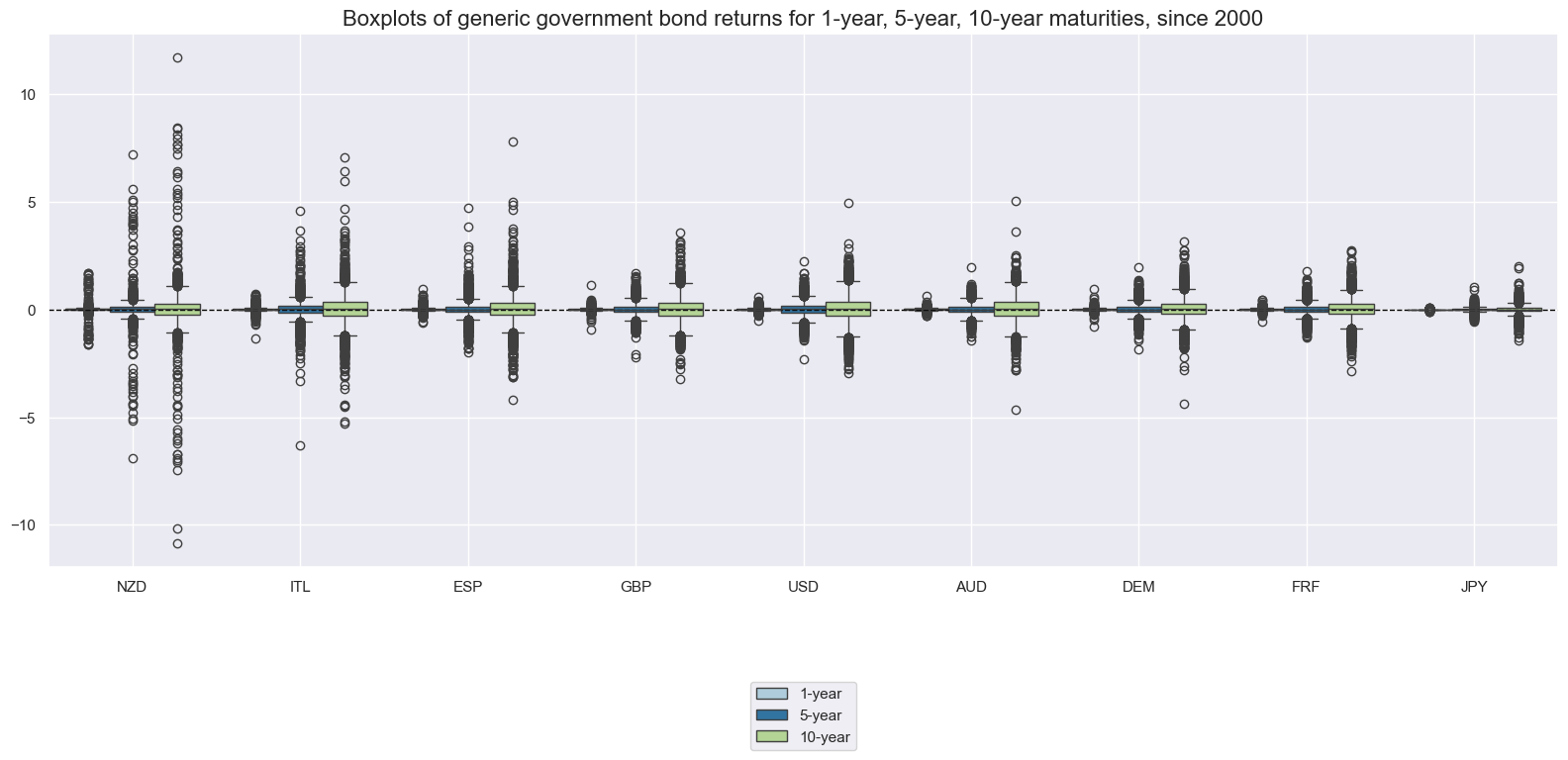
Bond returns have displayed broadly similar market phases across tenors and countries. However, return variances have been very different. Higher duration risk has translated into higher variance.
xcatx = ["GB01YR_NSA", "GB05YR_NSA", "GB10YR_NSA"]
cidx = cids
msp.view_ranges(
dfd,
xcats=xcatx,
cids=cids,
sort_cids_by="std",
start="2000-01-01",
kind="box",
title="Boxplots of generic government bond returns for 1-year, 5-year, 10-year maturities, since 2000",
xcat_labels=["1-year", "5-year", "10-year"],
size=(16, 8),
)
xcatx = ["GB01YR_NSA", "GB05YR_NSA", "GB10YR_NSA"]
cidx = cids
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="2000-01-01",
title="Cumulative generic government bond returns for 1-year, 5-year, 10-year maturities",
title_adj=1.05,
title_xadj=0.455,
title_fontsize=22,
legend_fontsize=17,
label_adj=0.2,
xcat_labels=["1-year", "5-year", "10-year"],
cumsum=True,
ncol=3,
same_y=False,
size=(12, 7),
aspect=1.7,
all_xticks=True,
)
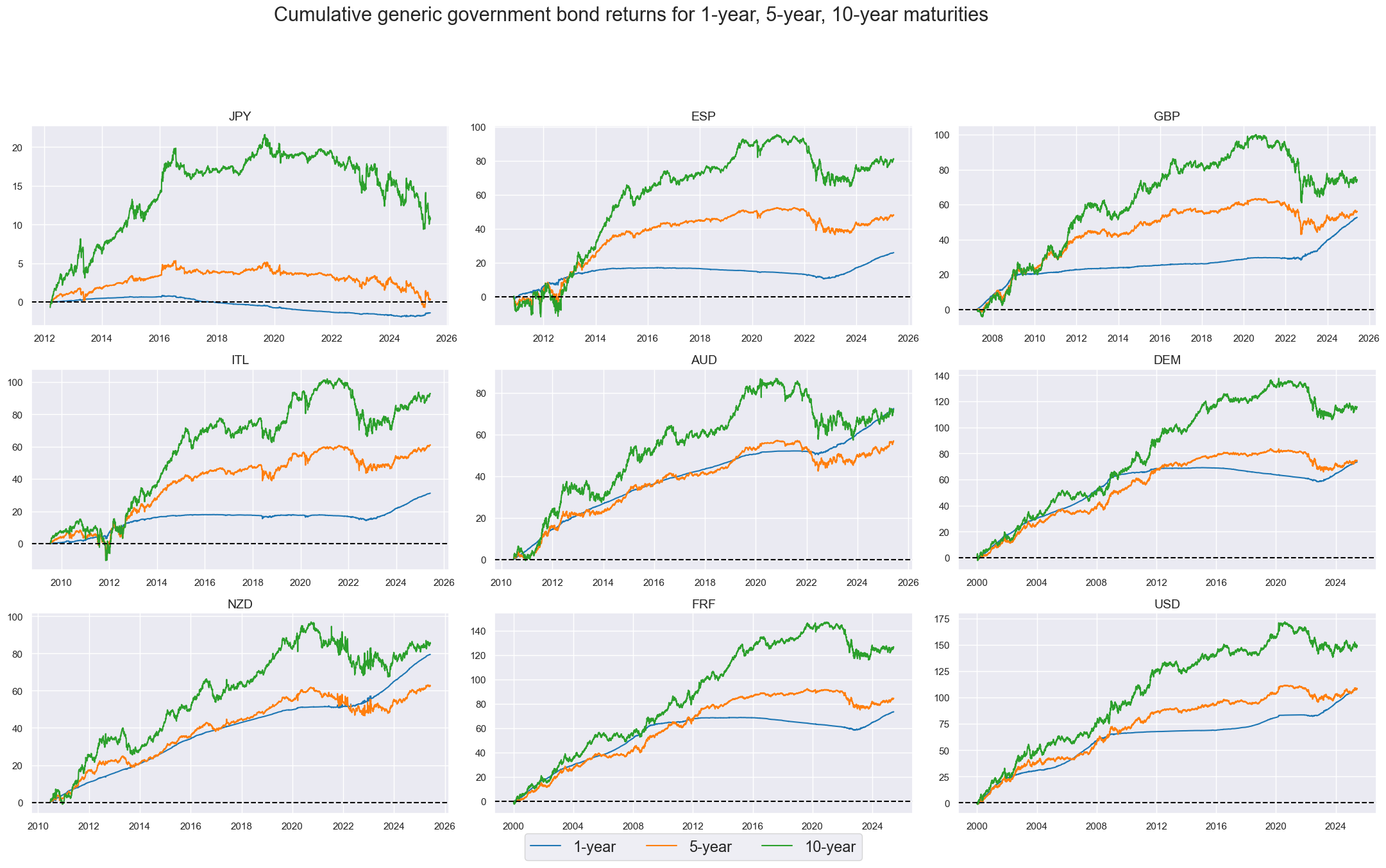
xcatx = ["GB01YR_NSA", "GB05YR_NSA", "GB10YR_NSA", "GB30YR_NSA"]
cidx = ["USD"]
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="1990-01-01",
title="USD: Cumulative generic government bond returns for 1-year, 5-year, 10-year and 30-year maturities",
title_adj=1.02,
xcat_labels=["1-year", "5-year", "10-year", "30-year"],
cumsum=True,
ncol=1,
same_y=False,
size=(12, 7),
aspect=1.7,
)
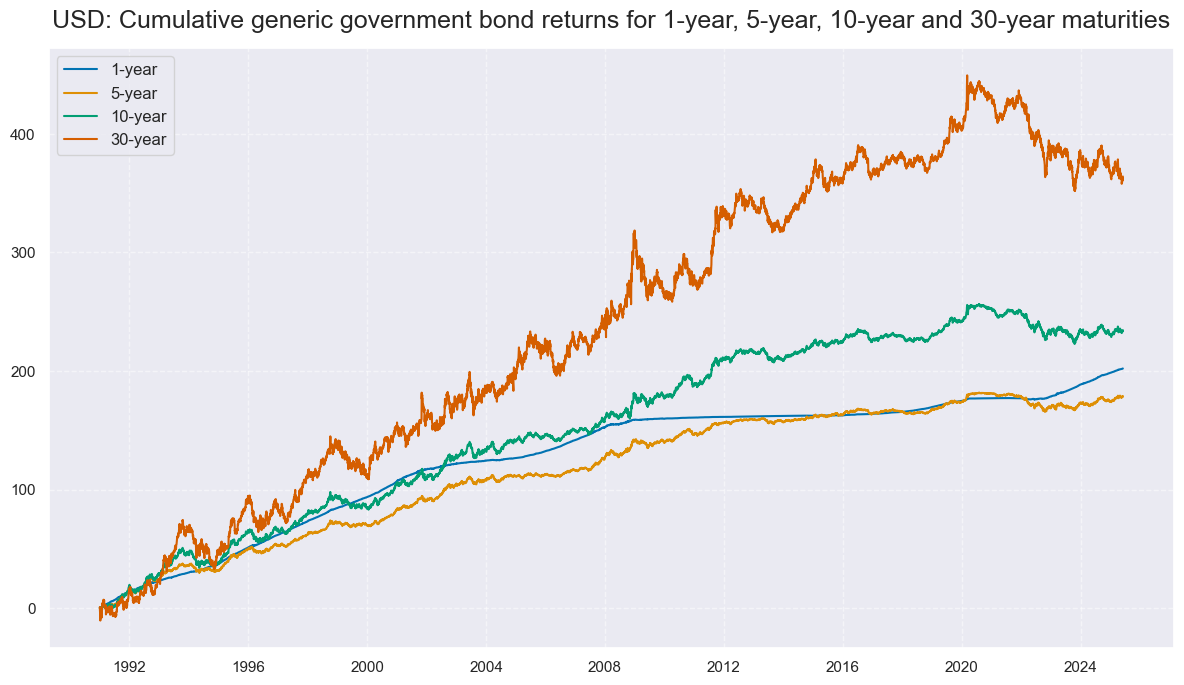
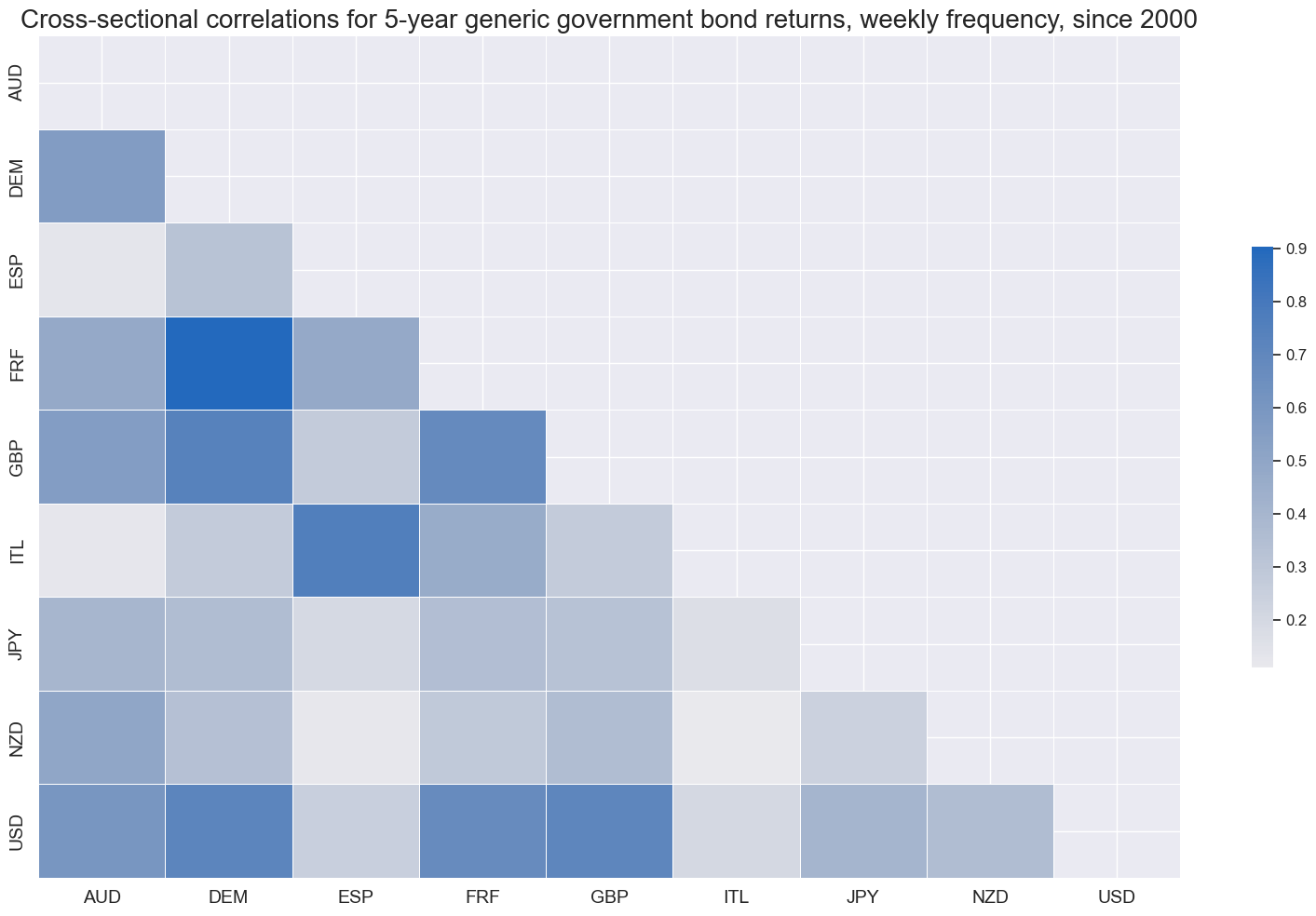
Returns have been positively correlated across issuers and tenors, even at higher frequencies.
xcatx = ["GB05YR_NSA"]
cidx = cids
msp.correl_matrix(
dfd,
xcats=xcatx,
cids=cids,
freq="W",
size=(16, 10),
title="Cross-sectional correlations for 5-year generic government bond returns, weekly frequency, since 2000",
)
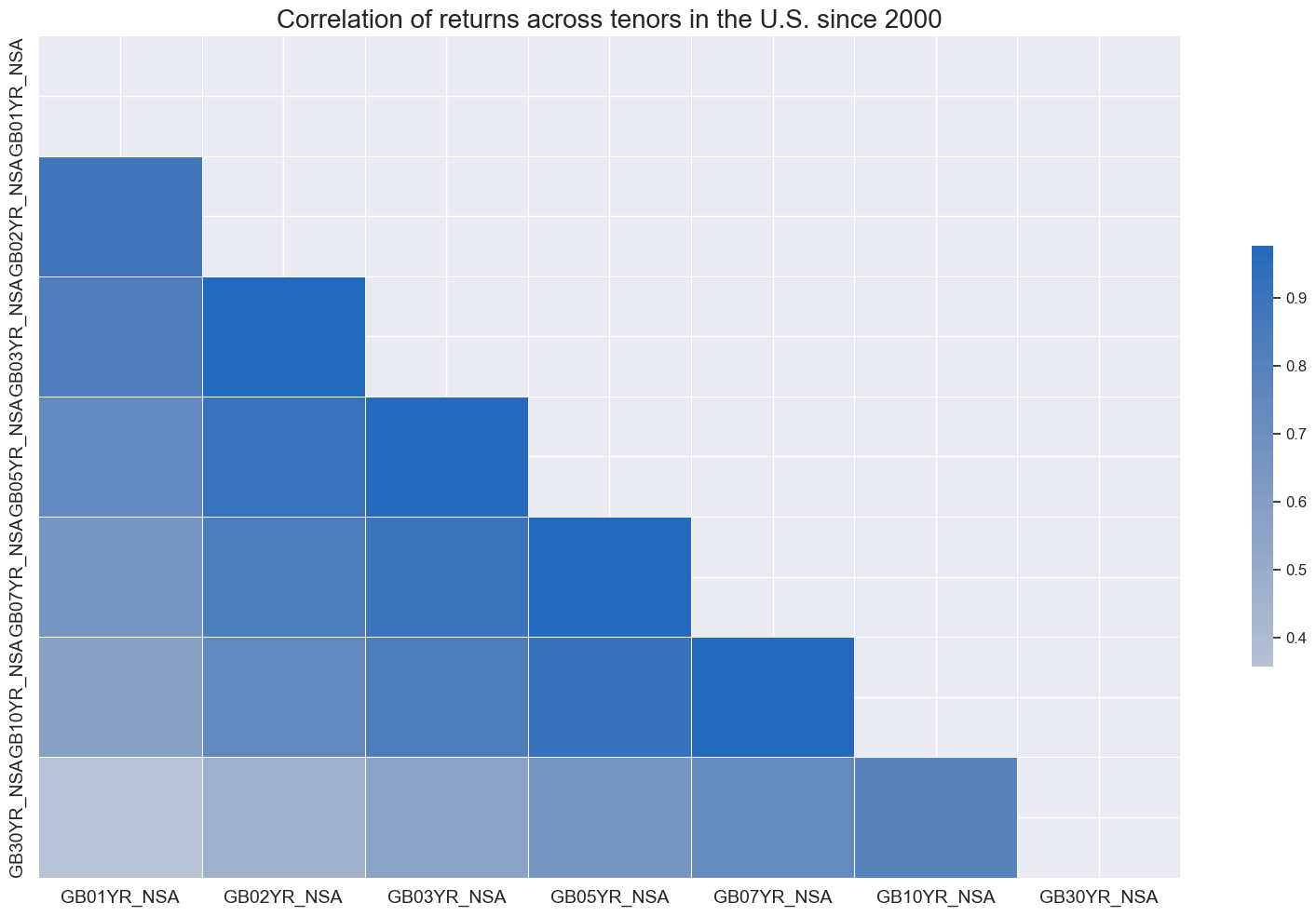
In the United States, government bond return series have been positively correlated across tenors.
xcatx = [
"GB01YR_NSA",
"GB02YR_NSA",
"GB03YR_NSA",
"GB05YR_NSA",
"GB07YR_NSA",
"GB10YR_NSA",
"GB30YR_NSA",
]
cidx = ["USD"]
msp.correl_matrix(
dfd,
xcats=xcatx,
cids=cidx,
size=(16, 10),
title="Correlation of returns across tenors in the U.S. since 2000",
)
Government bond excess returns #
Excess returns show similar patterns but deviate over longer periods with positive nominal short-term rates, due to funding costs.
xcatx = ["GB05YR_NSA", "GB05YXR_NSA"]
cidx = cids
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="2000-01-01",
title="Cumulative generic government bond returns and excess returns, 5-year tenor",
title_fontsize=25,
legend_fontsize=17,
title_adj=1.05,
title_xadj=0.45,
label_adj=0.15,
xcat_labels=["Cash return", "Excess return"],
cumsum=True,
ncol=3,
same_y=False,
size=(12, 7),
aspect=1.7,
all_xticks=True,
)
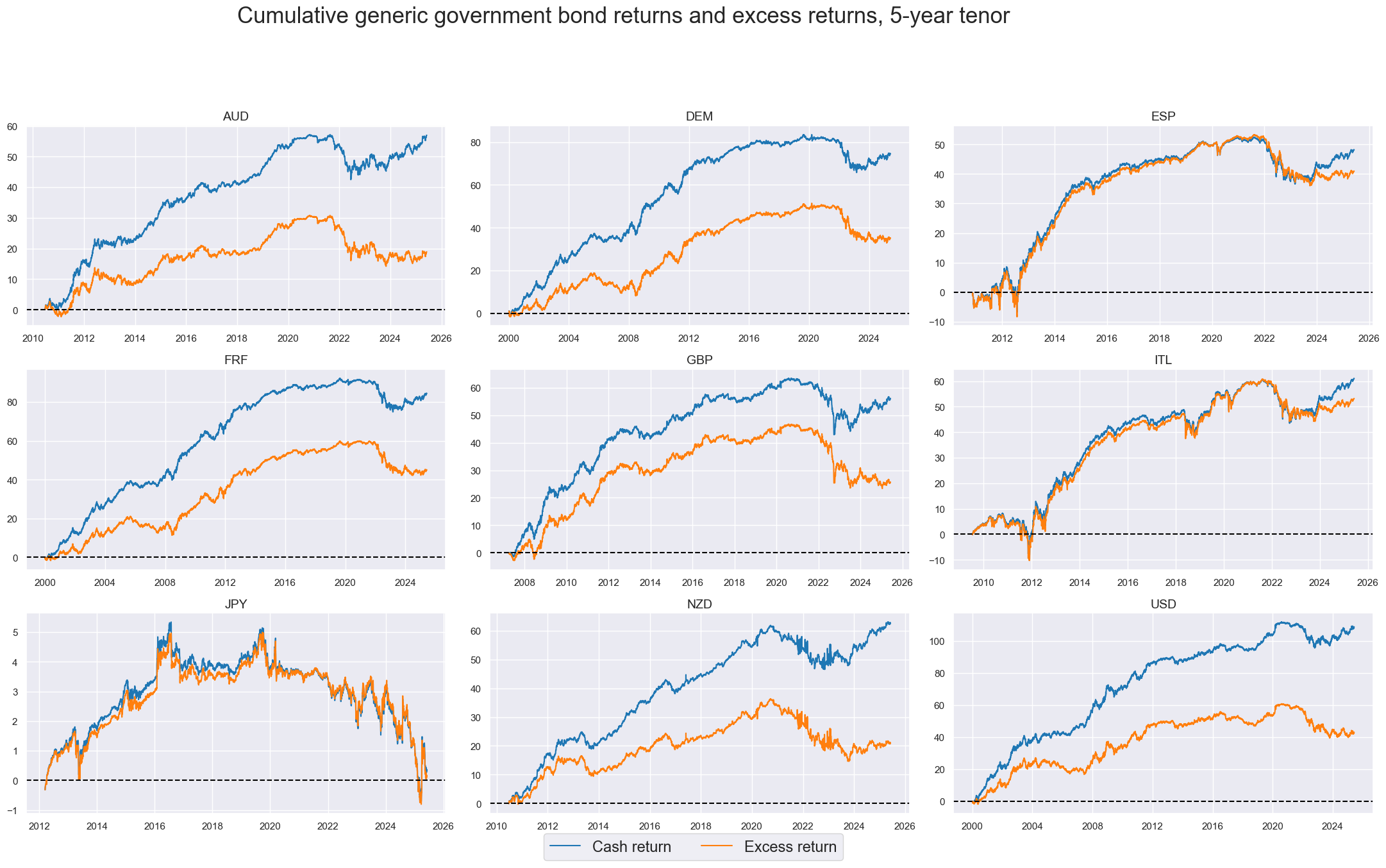
xcatx = ["GB05YR_NSA", "GB05YXR_NSA"]
cidx = ["USD"]
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="1990-01-01",
title="USD: Cumulative generic government bond returns and excess returns, 5-year tenor",
title_adj=1.02,
cumsum=True,
ncol=1,
same_y=False,
size=(12, 7),
aspect=1.7,
)
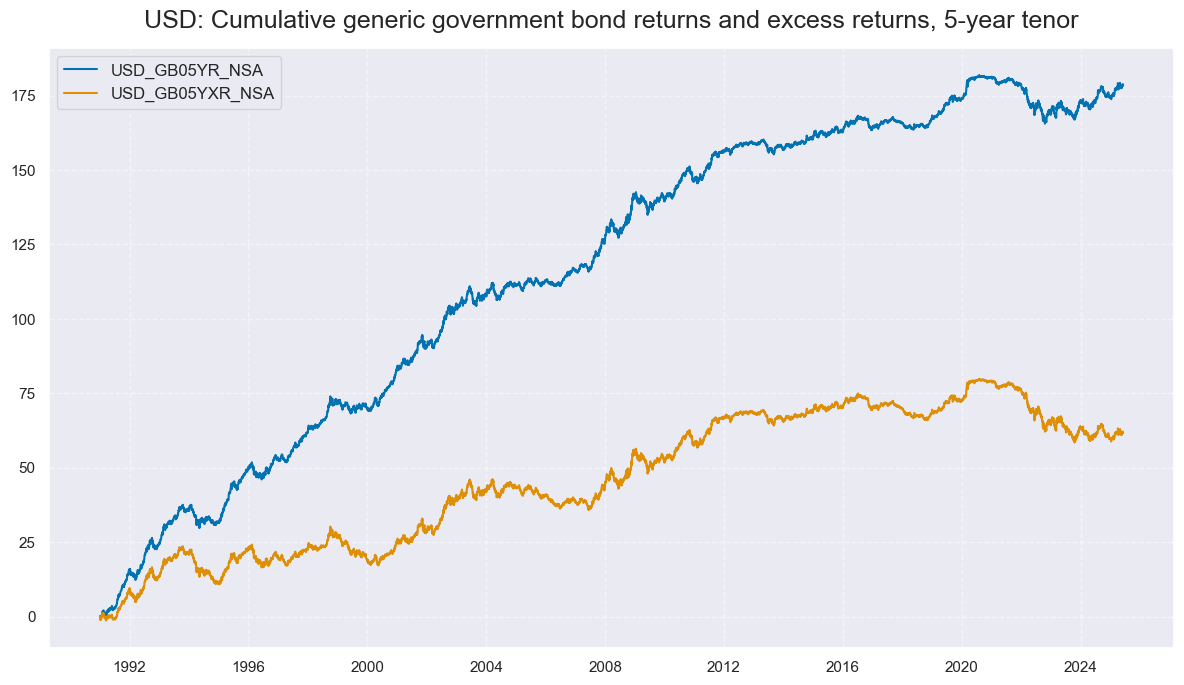
Vol-targeted government bond excess returns #
Volatility-targeting makes returns more comparable across tenors and countries.
xcatx = ["GB05YXR_NSA", "GB05YXR_VT10"]
cidx = cids
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="2000-01-01",
title="Cumulative generic government bond returns, 5-year tenor",
title_fontsize=27,
legend_fontsize=17,
title_adj=1.05,
title_xadj=0.425,
label_adj=0.175,
xcat_labels=["Nominal excess return", "Vol-targeted excess return"],
cumsum=True,
ncol=3,
same_y=False,
size=(12, 7),
aspect=1.7,
all_xticks=True,
)
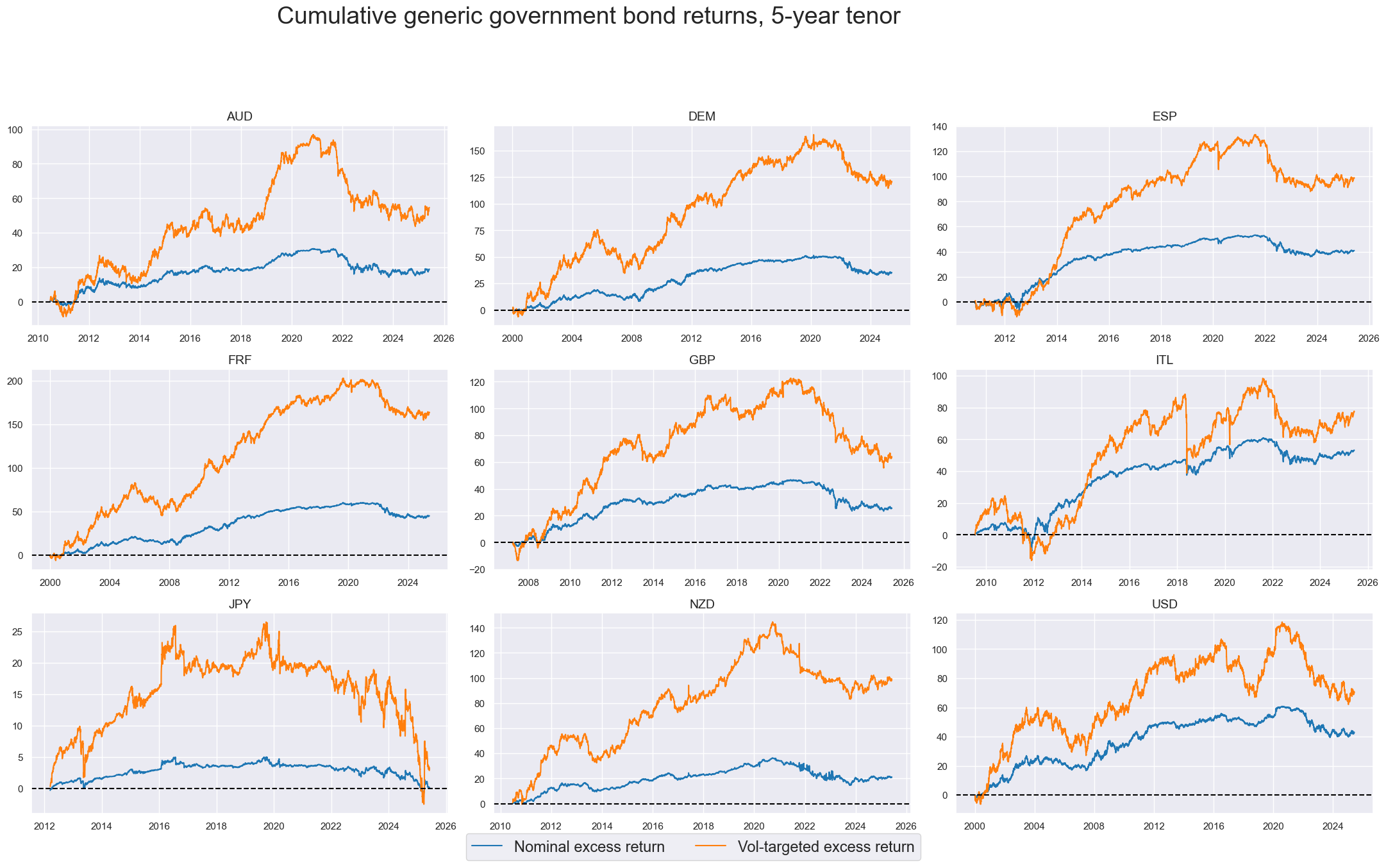
Vol-targeted positions across different tenors would still have mostly produced outperformance of the longer-duration asset over past decades.
xcatx = ["GB02YXR_VT10", "GB05YXR_VT10", "GB10YXR_VT10"]
cidx = cids
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="2000-01-01",
title="Cumulative excess government bond returns, 10% vol-target, for 2-year, 5-year and 10-year maturities",
title_fontsize=27,
legend_fontsize=17,
xcat_labels=["2-year", "5-year", "10-year"],
title_adj=1.05,
label_adj=0.2,
cumsum=True,
ncol=3,
same_y=False,
size=(12, 7),
aspect=1.7,
all_xticks=True,
)
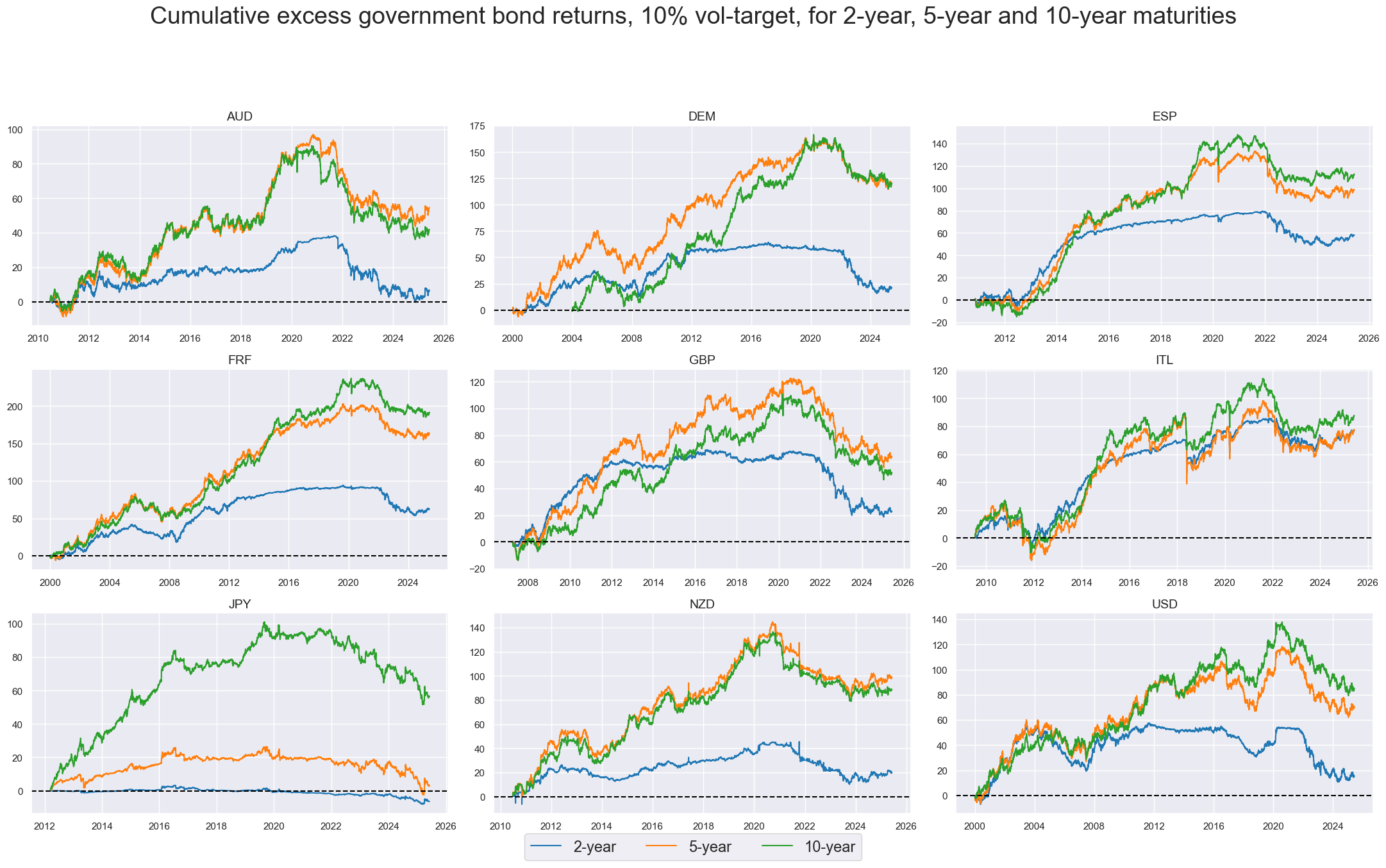
Government bond future (excess) returns #
The broad pattern of futures returns looks similar to cash returns. However, there can be significant short- and long-term differences, as shown by the USD history.
xcatx = ["GBF02YXR_NSA", "GBF05YXR_NSA", "GBF10YXR_NSA"]
cidx = cids
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="2000-01-01",
title="Government bond future excess returns for 2-year, 5-year and 10-year tenors",
title_adj=1.05,
title_xadj=0.46,
title_fontsize=27,
legend_fontsize=17,
xcat_labels=["2-year", "5-year", "10-year"],
label_adj=0.2,
cumsum=True,
ncol=3,
same_y=False,
size=(12, 7),
aspect=1.7,
all_xticks=True,
)
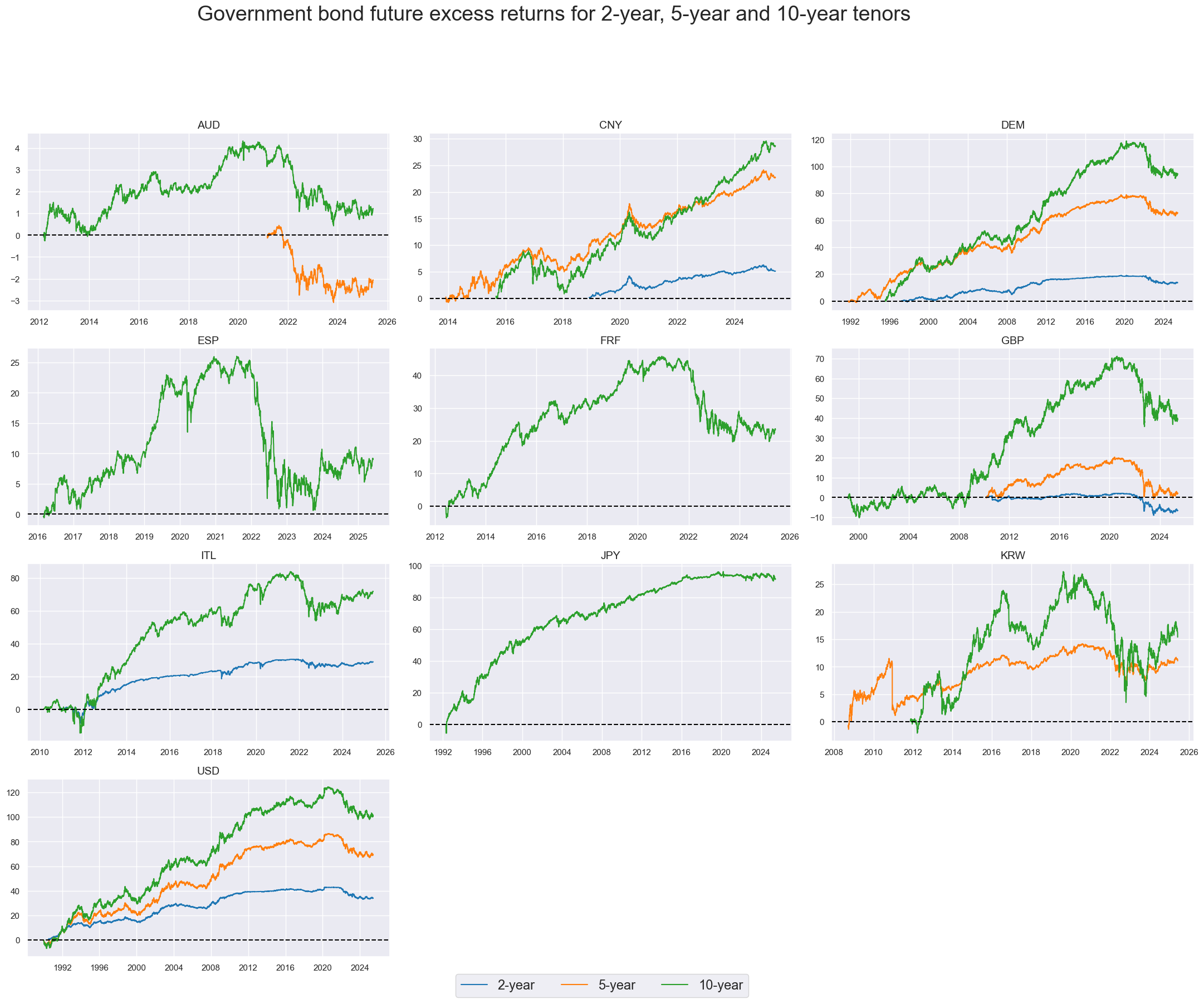
There can be substantial differences in excess bond returns (funded) and futures. Government bond futures have an underlying basket of bonds whose prices adjust according to the ‘cheapest to deliver’ within the basket. For a 10-year U.S. treasury bond future, for example, the basket of bonds could comprise tens of bonds in the 10-year area. In fact, the basket accepts bonds from 6.5 years to maturity and the cheapest to deliver could very well be an 7 year bond. Hence, the compounded returns over a long period of time between the cheapest to deliver (expressed by the excess returns of our futures) and those of our generic bonds (which are constant-maturity by definition) can diverge.
In addition, we note that the excess returns coming from our bonds are calculated upon synthetic future prices coming from spot curves, and hence add to the tracking error volatility.
Sources:
-
http://www.yieldcurve.com/mktresearch/files/futuresbondbasis_part1.pdf
-
https://www.cmegroup.com/markets/interest-rates/us-treasury/10-year-us-treasury-note.contractSpecs.html
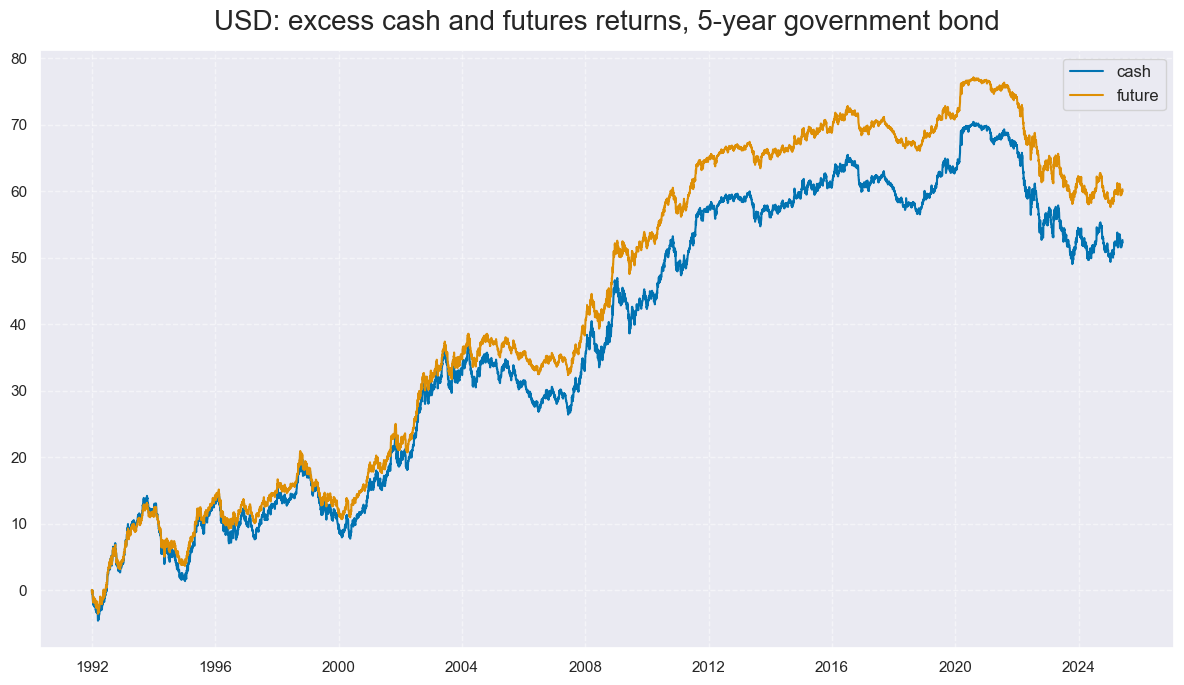
xcatx = ["GB05YXR_NSA", "GBF05YXR_NSA"]
cidx = ["USD"]
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start="2000-01-01",
title="USD: excess cash and futures returns, 5-year government bond",
title_fontsize=20,
title_adj=1.02,
xcat_labels=["cash", "future"],
cumsum=True,
ncol=1,
same_y=False,
size=(12, 7),
aspect=1.7,
)
Importance #
Research links #
The importance of carry trades in the bond market has been most popular in periods characterised by a lower concentration of market-changing events and lower inflation. This is due to the fact that in such instances, the probability of losing one’s return due to adverse yield movements or higher inflation is lower. For instance, after covid, especially in the summer months, carry trades - in the italian market in particular - were popular. Fitch ratings .
Of course bonds return and the expected carry depends largely on the general level of interest rates and in particular on the funding levels present in the market. For instance, after the Italian debt crisis in 2011, shortly after the arrival of the new Italian PM Mario Monti, government bond yields were still high however funding rates at the ECB were low. This spurred a resurgence of the carry trade, as detailed at the time on Reuters .
Bond carry has not observed large popularity in the literature however indeed it is among the main drivers of portfolio allocation. A strategy whereby portfolio construction was based on carry by selecting bonds with the highest expected bond risk premium per unit duration showed to have a low correlation with other strategies, thus “resulting in a global curve carry factor that has a significant positive risk-adjusted performance” Duyvesteyn et al.
Empirical clues #
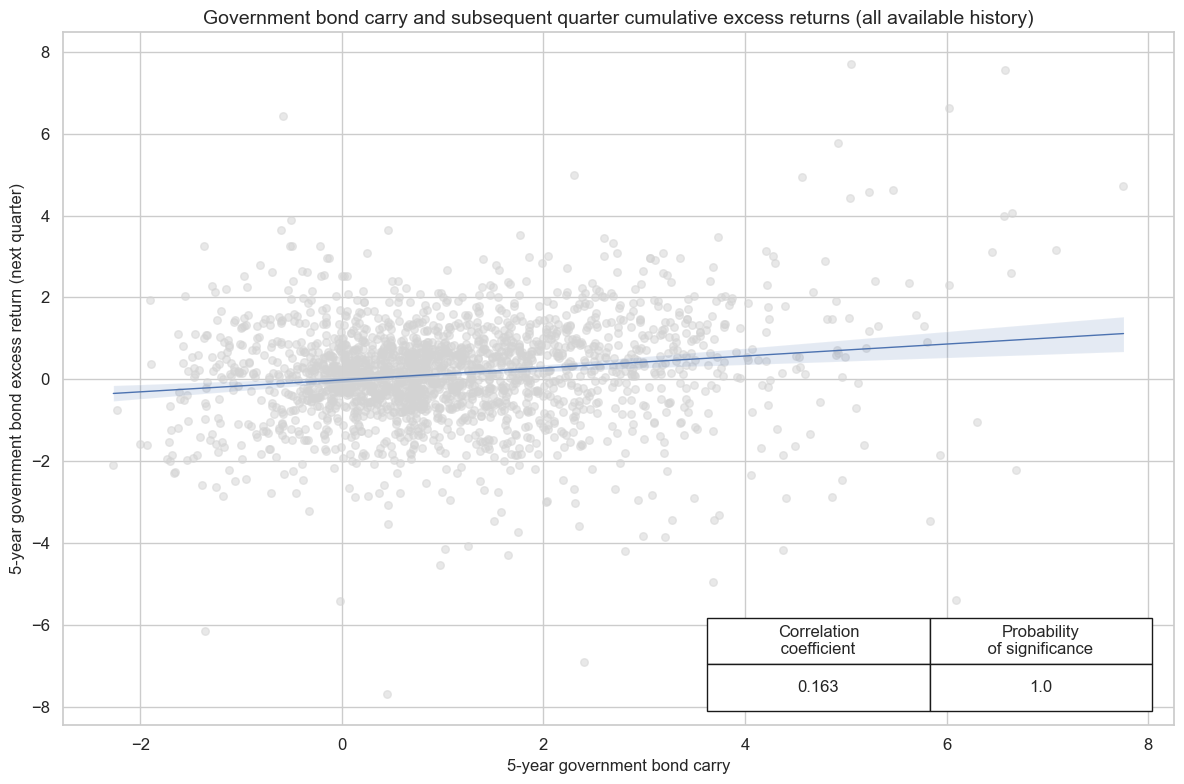
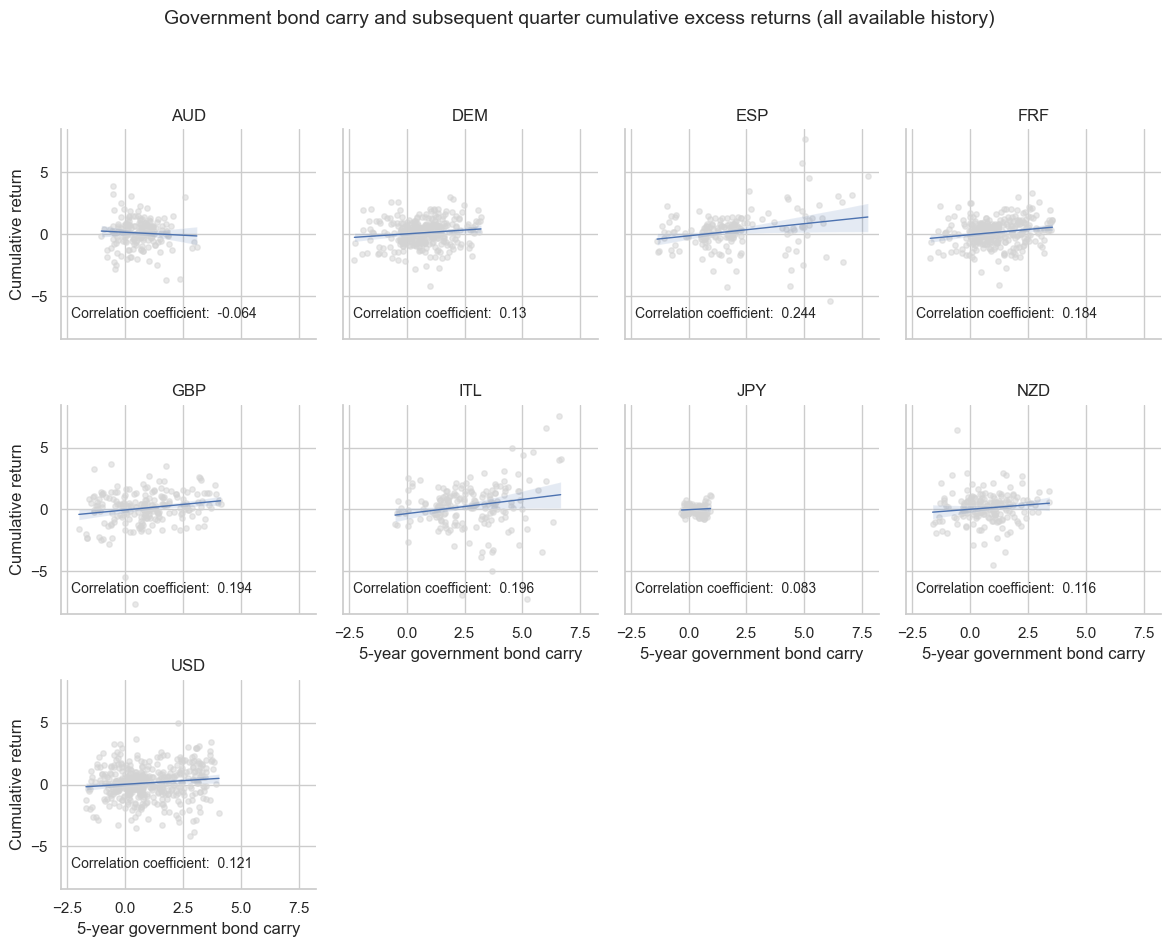
Historically, there has been a positive correlation between government bond carry and subsequent returns. This association is consistent across most currency areas, particularly across European nations.
xcatx = ["GB05YCRY_NSA", "GB05YXR_NSA"]
cidx = cids
cr = msp.CategoryRelations(
dfd,
xcats=xcatx,
cids=cidx,
freq="M",
lag=1,
xcat_aggs=["last", "sum"],
start="1990-01-01",
years=None,
)
cr.reg_scatter(
title="Government bond carry and subsequent quarter cumulative excess returns (all available history)",
labels=False,
coef_box="lower right",
ylab="5-year government bond excess return (next quarter)",
xlab="5-year government bond carry",
prob_est="map",
)
xcatx = ["GB05YCRY_NSA", "GB05YXR_NSA"]
cidx = cids
cr = msp.CategoryRelations(
dfd,
xcats=xcatx,
cids=cidx,
freq="M",
lag=1,
xcat_aggs=["last", "sum"],
start="1990-01-01",
years=None,
)
cr.reg_scatter(
title="Government bond carry and subsequent quarter cumulative excess returns (all available history)",
labels=False,
coef_box="lower right",
title_adj=1.05,
ylab="Cumulative return",
xlab="5-year government bond carry",
prob_est="map",
separator="cids",
)
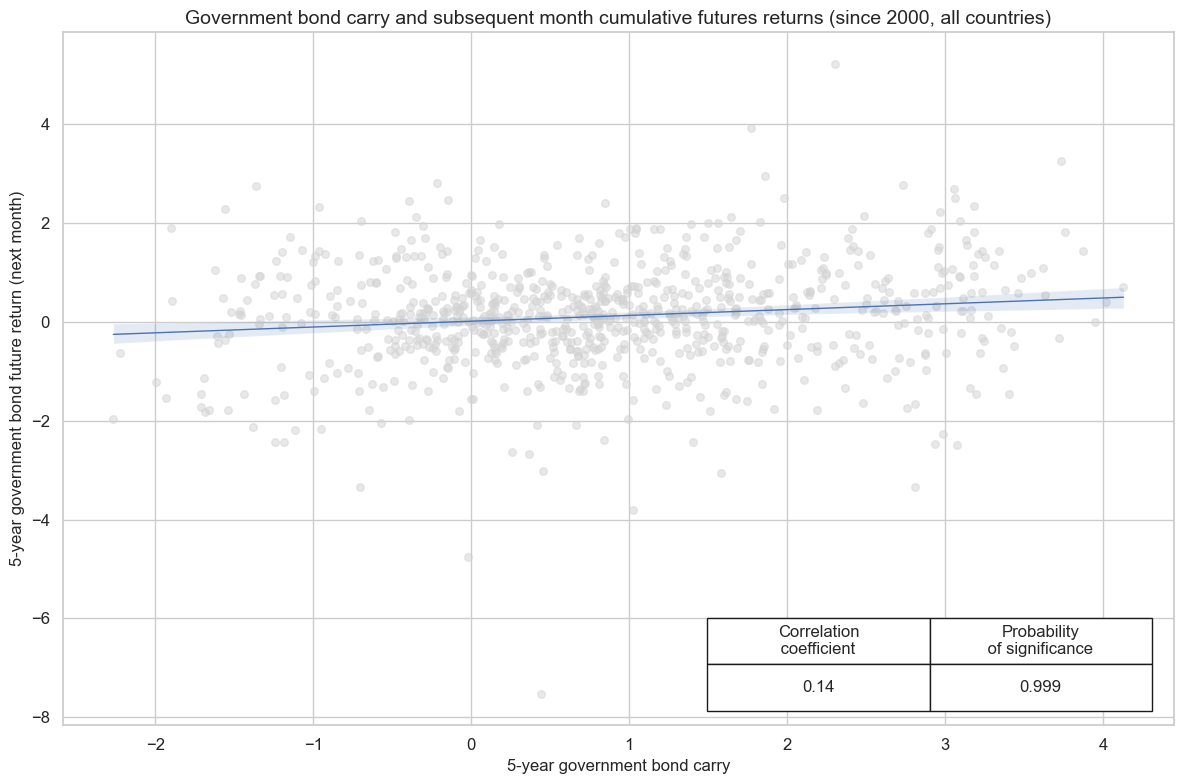
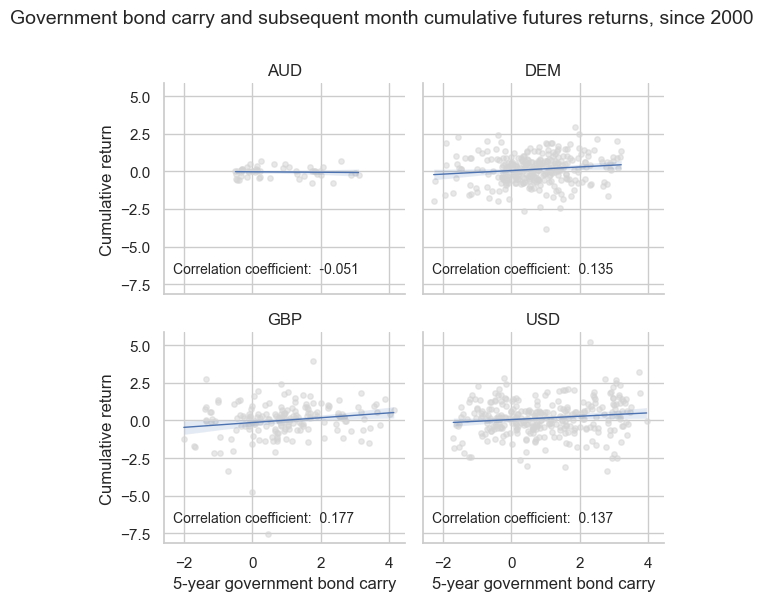
A similar relation exists between bond carry and subsequent futures return. The positive correlation is consistent across most available currency areas. The only exception is Australia, which has a very short 5-year futures history, starting in 2021.
xcatx = ["GB05YCRY_NSA", "GBF05YXR_NSA"]
cidx = cids
cr = msp.CategoryRelations(
dfd,
xcats=xcatx,
cids=cidx,
freq="M",
lag=1,
xcat_aggs=["last", "sum"],
start="2000-01-01",
years=None,
)
GBF05YXR_NSA misses: ['ESP', 'FRF', 'ITL', 'JPY', 'NZD'].
cr.reg_scatter(
title="Government bond carry and subsequent month cumulative futures returns (since 2000, all countries)",
labels=False,
coef_box="lower right",
ylab="5-year government bond future return (next month)",
xlab="5-year government bond carry",
prob_est="map",
)
xcatx = ["GB05YCRY_NSA", "GBF05YXR_NSA"]
cidx = cids
cr = msp.CategoryRelations(
dfd,
xcats=xcatx,
cids=cidx,
freq="M",
lag=1,
xcat_aggs=["last", "sum"],
start="2000-01-01",
years=None,
)
GBF05YXR_NSA misses: ['ESP', 'FRF', 'ITL', 'JPY', 'NZD'].
cr.reg_scatter(
title="Government bond carry and subsequent month cumulative futures returns, since 2000",
labels=False,
coef_box="lower right",
ylab="Cumulative return",
xlab="5-year government bond carry",
prob_est="map",
separator="cids",
)
Appendices #
Appendix 1: Calculation of total and excess generic bond returns #
The spot price of a zero-coupon bond with face value of 1 at the end of day t and with maturity of m days is naturally given by the following equation:
where m is the time to maturity in trading days, t the day at the very end of which prices and yields are recorded, and \(y_{m,t}\) is the annualized zero-coupon bond yield of a bond with m periods to maturity at time t. Analogously, the one-period futures price for a contract where the underlying currently has maturity m is given by the below equation:
where \(r^{(f)}_{t}\) is the annualized short-term funding rate, typically approximated by the local interbank or a collateralized funding rate.
The total return of a zero-coupon bond with a face value of 1 is simply the ratio of the price today versus the price yesterday:
The excess return of a zero-coupon bond yield with face value of 1 is:
Appendix 2: Currency symbols #
The word ‘cross-section’ refers to currencies, currency areas or economic areas. In alphabetical order, these are AUD (Australian dollar), BRL (Brazilian real), CAD (Canadian dollar), CHF (Swiss franc), CLP (Chilean peso), CNY (Chinese yuan renminbi), COP (Colombian peso), CZK (Czech Republic koruna), DEM (German mark), ESP (Spanish peseta), EUR (Euro), FRF (French franc), GBP (British pound), HKD (Hong Kong dollar), HUF (Hungarian forint), IDR (Indonesian rupiah), ITL (Italian lira), JPY (Japanese yen), KRW (Korean won), MXN (Mexican peso), MYR (Malaysian ringgit), NLG (Dutch guilder), NOK (Norwegian krone), NZD (New Zealand dollar), PEN (Peruvian sol), PHP (Phillipine peso), PLN (Polish zloty), RON (Romanian leu), RUB (Russian ruble), SEK (Swedish krona), SGD (Singaporean dollar), THB (Thai baht), TRY (Turkish lira), TWD (Taiwanese dollar), USD (U.S. dollar), ZAR (South African rand).
