FX forward carry

The category group contains nominal and real carry measures for FX forward contracts of global currencies versus their respective dominant cross (typically USD or EUR or a basket of both). All measures are annualized.

FX forward nominal carry of going long the base currency is calculated from the covered interest parity no-arbitrage condition in two steps:

First, similar to the J.P. Morgan FX Total Return Indices , we calculate the implied yield:

(3) \[\begin{equation} \hat{i}_{CCY} = \left( \frac{100}{h_{CCY}} \right) \cdot \left[ \left( \frac{S_{\text{CCY}/\text{DOM}}}{F_{\text{CCY}/\text{DOM}}} \right) \cdot \left(1 + \frac{i_{\text{DOM}} \cdot h_{DOM}}{100} \right) - 1 \right] \end{equation}\]

Where \(S_{\text{CCY}/\text{DOM}}\) is the FX spot price vs dominant cross, \(F_{\text{CCY}/\text{DOM}}\) is the forward contract, \(i_{DOM}\) is the interest rate of the dominant cross taken as the mid-market swap yield for the maturity, and \(h\) is the tenor of the forward contract expressed in fraction of years following each currency day count convention (CCY or DOM). To calculate \(h\) , we take into account the FX forwards horizon dates, CCY and DOM holidays, and day count conventions (more information on Appendix 2 ). The only expection to the above is BRL, which uses exponential interpolation instead of linear interpolation ( Appendix 3 ).

Second, we calculate annualized carry as the difference between the implied yield and interest rate for the dominant cross.

(4) \[\begin{equation} CRY_{t} = \hat{i}_{CCY} - i_\text{DOM} \end{equation}\]

The FX spot and forward prices are from the JPMorgan trading desks, with Asian, European, and USDCAD taken at London close. Latin American FX crosses (USDBRL, USDCLP, USDCOP, USDMXN, and USDPEN) are end-of-day mark of each country’s trading desk.

Nominal carry versus dominant cross (no hedges)

Ticker : FXCRY_NSA / FXCRY_VT10

Label : Nominal forward-implied carry vs. dominant cross: % ar / % ar for 10% vol target.

Definition : 1-month FX forward carry against dominant cross(es), % annualized: based on notional of the contract / based on risk capital on position scaled to 10% (annualized) volatility target.

Notes :

• The carry metric is calculated for a contract that is long the local currency of the cross-section against its dominant traded benchmark(s). For most currencies, the benchmark is the dollar. For some European currencies (CHF, CZK, HUF, NOK, PLN, RON, SEK), the benchmark is the euro. For GBP, TRY, and RUB, an equally weighted basket of dollar and euro is used.

• For the following currencies, returns are based on non-deliverable contracts: IDR, INR, KRW, CNY, MYR, and TWD.

• Volatility-targeted carry positions are scaled to a 10% annualized standard deviation target, estimated based on an exponential moving average of daily returns with a half-life of 11 days. Positions are rebalanced at the end of each month. Also, a maximum leverage ratio of 5 (of implied notional to cash position) has been imposed.

• For some currencies, carry data include periods of low liquidity and FX targeting. If one wishes to ‘blacklist’ such periods one should use the non-tradability and FX-target dummmies, which have category ticker codes FXUNTRADABLE_NSA and FXTARGETED_NSA .

Nominal carry versus dominant cross for longer tenors

Ticker : FX03MCRY_NSA / FX06MCRY_NSA / FX09MCRY_NSA / FX01YCRY_NSA

Label : Nominal forward-implied carry vs. dominant cross, % ar : 3m tenor / 6m tenor / 9m tenor / 1y tenor.

Definition : FX forward carry against dominant cross(es), % annualized, based on notional of the contract: 3-month forward / 6-month forward / 9-month forward / 1-year forward.

Notes :

• The carry metric is calculated for a contract that is long the local currency of the cross-section against its dominant traded benchmark(s). For most currencies, the benchmark is the dollar. For some European currencies (CHF, CZK, HUF, NOK, PLN, RON, SEK), the benchmark is the euro. For GBP, TRY, and RUB, an equally weighted basket of dollar and euro is used.

• For the following currencies, returns are based on non-deliverable contracts: IDR, INR, KRW, CNY, MYR, and TWD.

• For some currencies, carry data include periods of low liquidity and FX targeting. If one wishes to ‘blacklist’ such periods one should use the non-tradability and FX-target dummmies, which have category ticker codes FXUNTRADABLE_NSA and FXTARGETED_NSA .

Vol-targeted nominal carry versus dominant cross for longer tenors

Ticker : FX03MCRY_VT10 / FX06MCRY_VT10 / FX09MCRY_VT10 / FX01YCRY_VT10

Label : Nominal forward-implied carry vs. dominant cross, % ar for 10% vol target : 3m tenor / 6m tenor / 9m tenor / 1y tenor.

Definition : FX forward carry against dominant cross(es), % annualized, based on risk capital on position scaled to 10% (annualized) volatility target: 3-month forward / 6-month forward / 9-month forward / 1-year forward.

Notes :

• The carry metric is calculated for a contract that is long the local currency of the cross-section against its dominant traded benchmark(s). For most currencies, the benchmark is the dollar. For some European currencies (CHF, CZK, HUF, NOK, PLN, RON, SEK), the benchmark is the euro. For GBP, TRY, and RUB, an equally weighted basket of dollar and euro is used.

• For the following currencies, returns are based on non-deliverable contracts: IDR, INR, KRW, CNY, MYR, and TWD.

• Volatility-targeted carry positions are scaled to a 10% annualized standard deviation target, estimated based on an exponential moving average of daily returns with a half-life of 11 days. Positions are rebalanced at the end of each month. Also, a maximum leverage ratio of 5 (of implied notional to cash position) has been imposed.

• For some currencies, carry data include periods of low liquidity and FX targeting. If one wishes to ‘blacklist’ such periods one should use the non-tradability and FX-target dummmies, which have category ticker codes FXUNTRADABLE_NSA and FXTARGETED_NSA .

Nominal carry versus USD or EUR (no hedges)

Ticker : FXCRYUSD_NSA / FXCRYUSD_VT10 / FXCRYEUR_NSA / FXCRYEUR_VT10

Label : Nominal forward-implied carry %ar: vs. USD / vs. USD for 10% vol target / vs. EUR / vs. EUR for 10% vol target.

Definition : 1-month FX forward carry, % annualized: against USD, based on notional of the contract / against USD, based on risk capital on position scaled to 10% (annualized) volatility target / against EUR, based on notional of the contract / against EUR, based on risk capital on position scaled to 10% (annualized) volatility target.

Notes :

• The carry metric is calculated for a contract that is long the local currency of the cross section against USD.

• For the following currencies, returns are based on non-deliverable contracts: IDR, INR, KRW, CNY, MYR, and TWD.

• Volatility-targeted carry positions are scaled to a 10% annualized standard deviation target, estimated based on an exponential moving average of daily returns with a half-life of 11 days. Positions are rebalanced at the end of each month. Also, a maximum leverage ratio of 5 (of implied notional to cash position) has been imposed.

• For some currencies, carry data include periods of low liquidity and FX targeting. If one wishes to ‘blacklist’ such periods one should use the non-tradability and FX-target dummmies, which have category ticker codes FXUNTRADABLE_NSA and FXTARGETED_NSA .

Nominal carry versus dominant cross (with hedges)

Ticker : FXCRYHvGDRB_NSA

Label : Nominal carry on 1-month FX forward position, hedged against market directional risk.

Definition : 1-month FX forward carry against dominant cross(es), % annualized, for a forward position that has been hedged against directional risk through a position in a global directional risk basket.

Notes :

• The global directional risk basket contains equal volatility-weighted positions in equity index futures, CDS indices and FX forwards. See also the notes for directional risk basket carry ( DRBCRY_NSA ) here .

• Hedge ratios are calculated based on historical “beta”, i.e. OLS regression coefficients of past forward returns with respect of global directional risk basket returns. The estimate uses two regressions. One is based on monthly returns with an exponentially-weighted lookback of 24 months half-life. The other is based on daily returns with exponentially-weighted lookback of 63 trading days. The usage of the two lookbacks seeks to strike a balance between timeliness of information and structural relations.

• See also related important notes on “Nominal carry metrics (no hedges)” ( FXCRY_NSA and FXCRY_VT10 ).

Real carry versus dominant cross (no hedges)

Ticker : FXCRR_NSA / FXCRR_VT10

Label : Real forward-implied carry vs. dominant cross: % ar / % ar for 10% vol target.

Definition : 1-month FX forward carry against dominant cross(es), % annualized and adjusted for expected inflation differential: based on notional of the contract / based on risk capital on position scaled to 10% (annualized) volatility target.

Notes :

• In contrast to nominal carry, real carry subtracts the differential between the expected local and benchmark inflation rate from annualized carry. The basis for the adjustment is the quantamental indicator “Estimated 1-year ahead inflation expectation” ( INFE1Y_JA ). The basis of these expectations are the dominant headline and core price indices (50-50) according to popular local conventions. Please check out the related notes in the section “Inflation expectations (Macrosynergy method)” here .

• See also related important notes on “Nominal carry metrics (no hedges)” ( FXCRY_NSA and FXCRY_VT10 ).

Real carry versus dominant cross for longer tenors

Ticker : FX03MCRR_NSA / FX06MCRR_NSA / FX09MCRR_NSA / FX01YCRR_NSA

Label : Real forward-implied carry vs. dominant cross, % ar : 3m tenor / 6m tenor / 9m tenor / 1y tenor.

Definition : FX forward carry against dominant cross(es), % annualized and adjusted for expected inflation differential, based on notional of the contract: 3-month forward / 6-month forward / 9-month forward / 1-year forward.

Notes :

• In contrast to nominal carry, real carry subtracts the differential between the expected local and benchmark inflation rate from annualized carry. The basis for the adjustment is the quantamental indicator “Estimated 1-year ahead inflation expectation” ( INFE1Y_JA ). The basis of these expectations are the dominant headline and core price indices (50-50) according to popular local conventions. Please check out the related notes in the section “Inflation expectations (Macrosynergy method)” here .

• See also related important notes on “Nominal carry metrics (no hedges)” ( FXCRY_NSA and FXCRY_VT10 ).

Vol-targeted real carry versus dominant cross for longer tenors

Ticker : FX03MCRR_VT10 / FX06MCRR_VT10 / FX09MCRR_VT10 / FX01YCRR_VT10

Label : Real forward-implied carry vs. dominant cross, % ar for 10% vol target: 3m tenor / 6m tenor / 9m tenor / 1y tenor.

Definition : FX forward carry against dominant cross(es), % annualized and adjusted for expected inflation differential, based on risk capital on position scaled to 10% (annualized) volatility target: 3-month forward / 6-month forward / 9-month forward / 1-year forward.

Notes :

• In contrast to nominal carry, real carry subtracts the differential between the expected local and benchmark inflation rate from annualized carry. The basis for the adjustment is the quantamental indicator “Estimated 1-year ahead inflation expectation” ( INFE1Y_JA ). The basis of these expectations are the dominant headline and core price indices (50-50) according to popular local conventions. Please check out the related notes in the section “Inflation expectations (Macrosynergy method)” here .

• See also related important notes on “Nominal carry metrics (no hedges)” ( FXCRY_NSA and FXCRY_VT10 ).

Real carry versus USD or EUR (no hedges)

Ticker : FXCRRUSD_NSA / FXCRRUSD_VT10 / FXCRREUR_NSA / FXCRREUR_VT10

Label : Real forward-implied carry %ar: vs. USD / vs. USD for 10% vol target / vs. EUR / vs. EUR for 10% vol target.

Definition : 1-month FX forward carry, % annualized and adjusted for expected inflation differential: against USD, based on notional of the contract / against USD, based on risk capital on position scaled to 10% (annualized) volatility target / against EUR, based on notional of the contract / against EUR, based on risk capital on position scaled to 10% (annualized) volatility target.

Notes :

• In contrast to nominal carry, real carry subtracts the differential between the expected local and benchmark inflation rate from annualized carry. The basis for the adjustment is the quantamental indicator “Estimated 1-year ahead inflation expectation” ( INFE1Y_JA ). Please check out related notes in the section “Inflation expectations (Macrosynergy method)” here .

• See also related important notes on “Nominal carry metrics (no hedges)” ( FXCRY_NSA and FXCRY_VT10 ).

Real carry versus dominant cross (with hedges)

Ticker : FXCRRHvGDRB_NSA

Label : Real carry on 1-month FX forward position, hedged against market directional risk.

Definition : 1-month FX forward carry against dominant cross(es), % annualized and adjusted for expected inflation differential, for a forward position that has been hedged against directional risk through a position in a global directional risk basket.

Notes :

• The global directional risk basket contains equal volatility-weighted positions in equity index futures, CDS indices and FX forwards. See also notes for directional risk basket carry ( DRBCRR_NSA ) here .

• Hedge ratios are calculated based on historical “beta”, i.e. OLS regression coefficients of past forward returns with respect of global directional risk basket returns. The estimate uses two regressions. One is based on monthly returns with an exponentially-weighted lookback of 24 months half-life. The other is based on daily returns with exponentially-weighted lookback of 63 trading days. The usage of the two lookbacks strikes a balance between timeliness of information and structural relations.

• See also related important notes on “Nominal carry metrics (no hedges)” ( FXCRY_NSA and FXCRY_VT10 ).

Imports

Only the standard Python data science packages and the specialized macrosynergy package are needed.

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math

import json
import yaml

import macrosynergy.management as msm
import macrosynergy.panel as msp
import macrosynergy.signal as mss
import macrosynergy.pnl as msn
import macrosynergy.visuals as msv

from macrosynergy.download import JPMaQSDownload

from timeit import default_timer as timer
from datetime import timedelta, date, datetime

import warnings

warnings.simplefilter("ignore")

The JPMaQS indicators we consider are downloaded using the J.P. Morgan Dataquery API interface within the macrosynergy package. This is done by specifying ticker strings , formed by appending an indicator category code <category> to a currency area code <cross_section> . These constitute the main part of a full quantamental indicator ticker, taking the form DB(JPMAQS,<cross_section>_<category>,<info>) , where <info> denotes the time series of information for the given cross-section and category. The following types of information are available:

• value giving the latest available values for the indicator

• eop_lag referring to days elapsed since the end of the observation period

• mop_lag referring to the number of days elapsed since the mean observation period

• grade denoting a grade of the observation, giving a metric of real time information quality.

After instantiating the JPMaQSDownload class within the macrosynergy.download module, one can use the download(tickers,start_date,metrics) method to easily download the necessary data, where tickers is an array of ticker strings, start_date is the first collection date to be considered and metrics is an array comprising the times series information to be downloaded.

cids_dmca = [
    "AUD",
    "CAD",
    "CHF",
    "EUR",
    "GBP",
    "JPY",
    "NOK",
    "NZD",
    "SEK",
    "USD",
]  # DM currency areas
cids_dmec = ["DEM", "ESP", "FRF", "ITL", "NLG"]  # DM euro area countries
cids_latm = ["BRL", "COP", "CLP", "MXN", "PEN"]  # Latam countries
cids_emea = ["CZK", "HUF", "ILS", "PLN", "RON", "RUB", "TRY", "ZAR"]  # EMEA countries
cids_emas = [
    "CNY",
    "HKD",
    "IDR",
    "INR",
    "KRW",
    "MYR",
    "PHP",
    "SGD",
    "THB",
    "TWD",
]  # EM Asia countries
cids_dm = cids_dmca + cids_dmec
cids_em = cids_latm + cids_emea + cids_emas
cids = sorted(cids_dm + cids_em)

main = [
    "FXCRR_NSA",
    "FX03MCRR_NSA", "FX06MCRR_NSA", "FX09MCRR_NSA", "FX01YCRR_NSA",
    "FXCRR_VT10",
    "FX03MCRR_VT10", "FX06MCRR_VT10", "FX09MCRR_VT10", "FX01YCRR_VT10",
    "FXCRRUSD_NSA",
    "FXCRRUSD_VT10",
    "FXCRREUR_NSA",
    "FXCRREUR_VT10",
    "FXCRY_NSA",
    "FX03MCRY_NSA", "FX06MCRY_NSA", "FX09MCRY_NSA", "FX01YCRY_NSA",
    "FXCRY_VT10",
    "FX03MCRY_VT10", "FX06MCRY_VT10", "FX09MCRY_VT10", "FX01YCRY_VT10",
    "FXCRYUSD_NSA",
    "FXCRYUSD_VT10",
    "FXCRYEUR_NSA",
    "FXCRYEUR_VT10",
    "FXCRRHvGDRB_NSA",
    "FXCRYHvGDRB_NSA",
]
econ = [
    "INTRGDPv5Y_NSA_P1M1ML12_3MMA",
    "INTRGDP_NSA_P1M1ML12_3MMA",
    "FXTARGETED_NSA",
    "FXUNTRADABLE_NSA",
]  # economic context
mark = [
    "FXXR_NSA",
    "FX03MXR_NSA",
    "FX06MXR_NSA",
    "FX09MXR_NSA",
    "FX01YXR_NSA",
    "FXXR_VT10",
    "FX03MXR_VT10",
    "FX06MXR_VT10",
    "FX09MXR_VT10",
    "FX01YXR_VT10",
    "FXXRHvGDRB_NSA",
]  # market links

xcats = main + econ + mark

# Download series from J.P. Morgan DataQuery by tickers

start_date = "1990-01-01"
tickers = [cid + "_" + xcat for cid in cids for xcat in xcats]
print(f"Maximum number of tickers is {len(tickers)}")

# Retrieve credentials

client_id: str = os.getenv("DQ_CLIENT_ID")
client_secret: str = os.getenv("DQ_CLIENT_SECRET")

# Download from DataQuery

with JPMaQSDownload(client_id=client_id, client_secret=client_secret) as downloader:
    start = timer()
    df = downloader.download(
        tickers=tickers,
        start_date=start_date,
        metrics=["value", "eop_lag", "mop_lag", "grading"],
        suppress_warning=True,
        show_progress=True,
    )
    end = timer()

dfd = df

print("Download time from DQ: " + str(timedelta(seconds=end - start)))

Maximum number of tickers is 1710

Downloading data from JPMaQS.
Timestamp UTC:  2025-07-30 12:21:09
Connection successful!

Requesting data: 100%|██████████| 342/342 [01:19<00:00,  4.31it/s]
Downloading data: 100%|██████████| 342/342 [01:59<00:00,  2.87it/s]

Some expressions are missing from the downloaded data. Check logger output for complete list.
1588 out of 6840 expressions are missing. To download the catalogue of all available expressions and filter the unavailable expressions, set `get_catalogue=True` in the call to `JPMaQSDownload.download()`.
Some dates are missing from the downloaded data. 
1 out of 9282 dates are missing.
Download time from DQ: 0:03:38.449788

Availability

cids_exp = sorted(
    list(set(cids) - set(["HKD", "USD", "DEM", "ESP", "FRF", "ITL", "NLG"]))
)  # cids expected in category panels
msm.missing_in_df(dfd, xcats=main, cids=cids_exp)

No missing XCATs across DataFrame.
Missing cids for FX01YCRR_NSA:     []
Missing cids for FX01YCRR_VT10:    []
Missing cids for FX01YCRY_NSA:     []
Missing cids for FX01YCRY_VT10:    []
Missing cids for FX03MCRR_NSA:     []
Missing cids for FX03MCRR_VT10:    []
Missing cids for FX03MCRY_NSA:     []
Missing cids for FX03MCRY_VT10:    []
Missing cids for FX06MCRR_NSA:     []
Missing cids for FX06MCRR_VT10:    []
Missing cids for FX06MCRY_NSA:     []
Missing cids for FX06MCRY_VT10:    []
Missing cids for FX09MCRR_NSA:     []
Missing cids for FX09MCRR_VT10:    []
Missing cids for FX09MCRY_NSA:     []
Missing cids for FX09MCRY_VT10:    []
Missing cids for FXCRREUR_NSA:     ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'COP', 'CZK', 'EUR', 'HUF', 'IDR', 'ILS', 'INR', 'JPY', 'KRW', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RON', 'SEK', 'SGD', 'THB', 'TWD', 'ZAR']
Missing cids for FXCRREUR_VT10:    ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'COP', 'CZK', 'EUR', 'HUF', 'IDR', 'ILS', 'INR', 'JPY', 'KRW', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RON', 'SEK', 'SGD', 'THB', 'TWD', 'ZAR']
Missing cids for FXCRRHvGDRB_NSA:  []
Missing cids for FXCRRUSD_NSA:     []
Missing cids for FXCRRUSD_VT10:    []
Missing cids for FXCRR_NSA:        []
Missing cids for FXCRR_VT10:       []
Missing cids for FXCRYEUR_NSA:     ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'COP', 'CZK', 'EUR', 'HUF', 'IDR', 'ILS', 'INR', 'JPY', 'KRW', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RON', 'SEK', 'SGD', 'THB', 'TWD', 'ZAR']
Missing cids for FXCRYEUR_VT10:    ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'COP', 'CZK', 'EUR', 'HUF', 'IDR', 'ILS', 'INR', 'JPY', 'KRW', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RON', 'SEK', 'SGD', 'THB', 'TWD', 'ZAR']
Missing cids for FXCRYHvGDRB_NSA:  []
Missing cids for FXCRYUSD_NSA:     []
Missing cids for FXCRYUSD_VT10:    []
Missing cids for FXCRY_NSA:        []
Missing cids for FXCRY_VT10:       []

History of nominal carry metrics begins mostly in the 1990s, with some EM countries only available from the early 2000s. Real carry metrics are mostly available from the first half of the 2000s.

For the explanation of currency symbols, which are related to currency areas or countries for which categories are available, please view Appendix 1 .

xcatx = main
cidx = cids_exp

dfx = msm.reduce_df(dfd, xcats=xcatx, cids=cidx)
dfs = msm.check_startyears(
    dfx,
)
msm.visual_paneldates(dfs, size=(20, 8))

print("Last updated:", date.today())

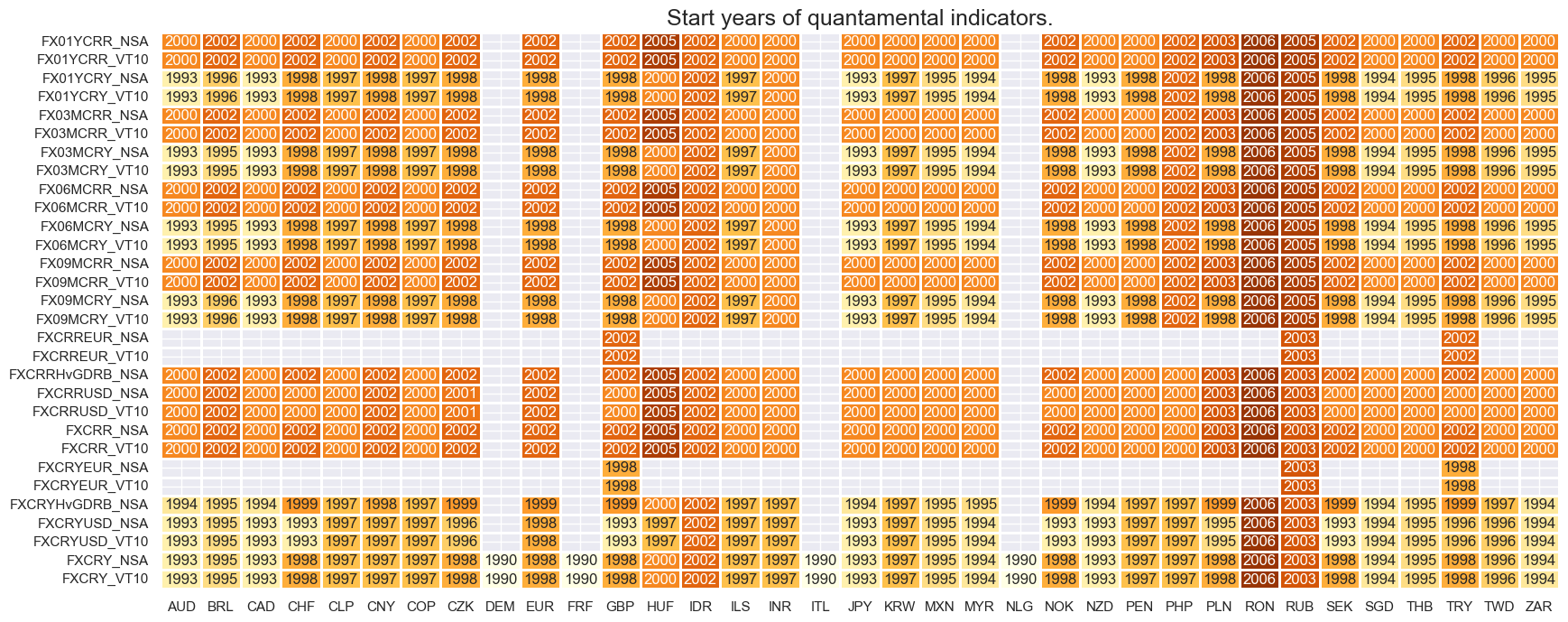
Last updated: 2025-07-30

plot = msp.heatmap_grades(
    dfd,
    xcats=main,
    cids=cids_exp,
    size=(19, 5),
    title=f"Average vintage grades from {start_date} onwards",
)

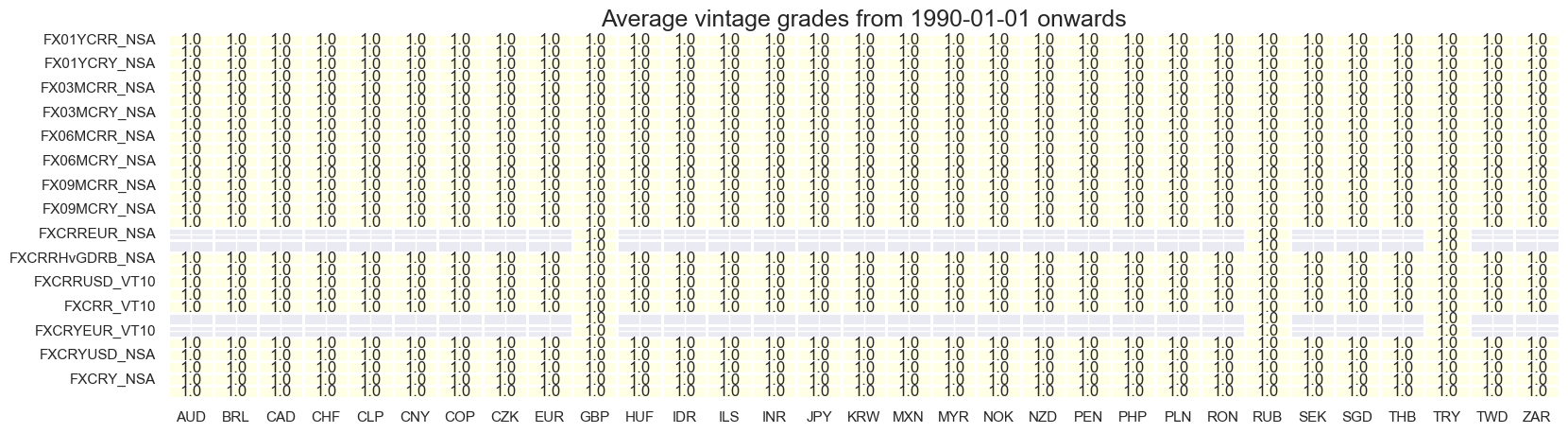
History

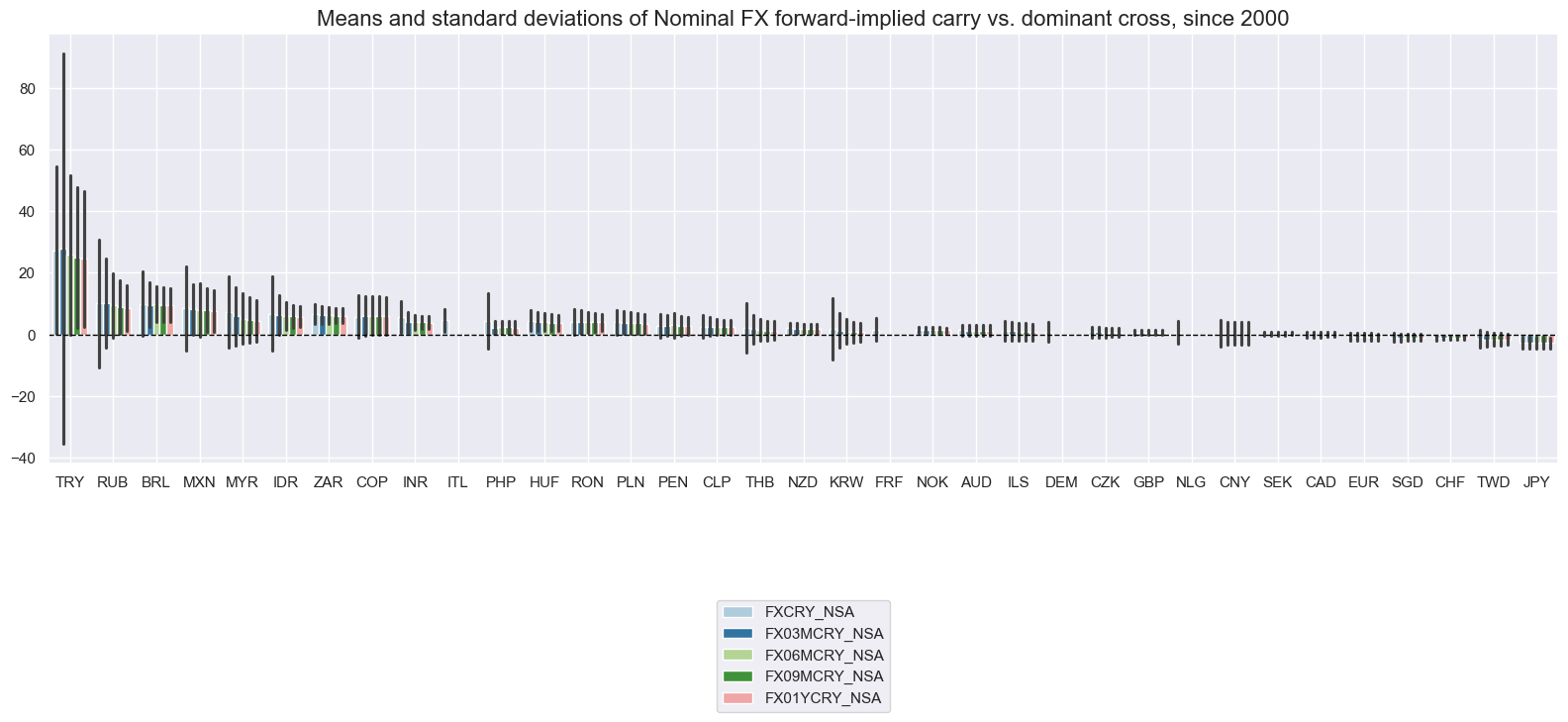
Nominal carry metrics (no hedges)

Nominal carry metrics and their variations have been very diverse across currencies. Equalizing targeted volatility makes a significant differences for carry both intertemporally, as it introduces much greater variation, and in cross-sectional comparison, as it penalizes currencies with large stop exchange rate fluctuations.

Carry metrics can be misleading for periods were currencies are not tradable or pegged, highlighting the importance of non-tradability and FX-target dummmies, which have category ticker codes FXUNTRADABLE_NSA and FXTARGETED_NSA in JPMaQS.

xcatx = [
    "FXCRY_NSA", "FX03MCRY_NSA", "FX06MCRY_NSA", "FX09MCRY_NSA", "FX01YCRY_NSA",
]
cidx = cids_exp

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    title="Means and standard deviations of Nominal FX forward-implied carry vs. dominant cross, since 2000",
    # xcat_labels=["Non-seasonally adjusted", "10% vol-target"],
    sort_cids_by="mean",
    start="1990-01-01",
    kind="bar",
    size=(16, 8),
)

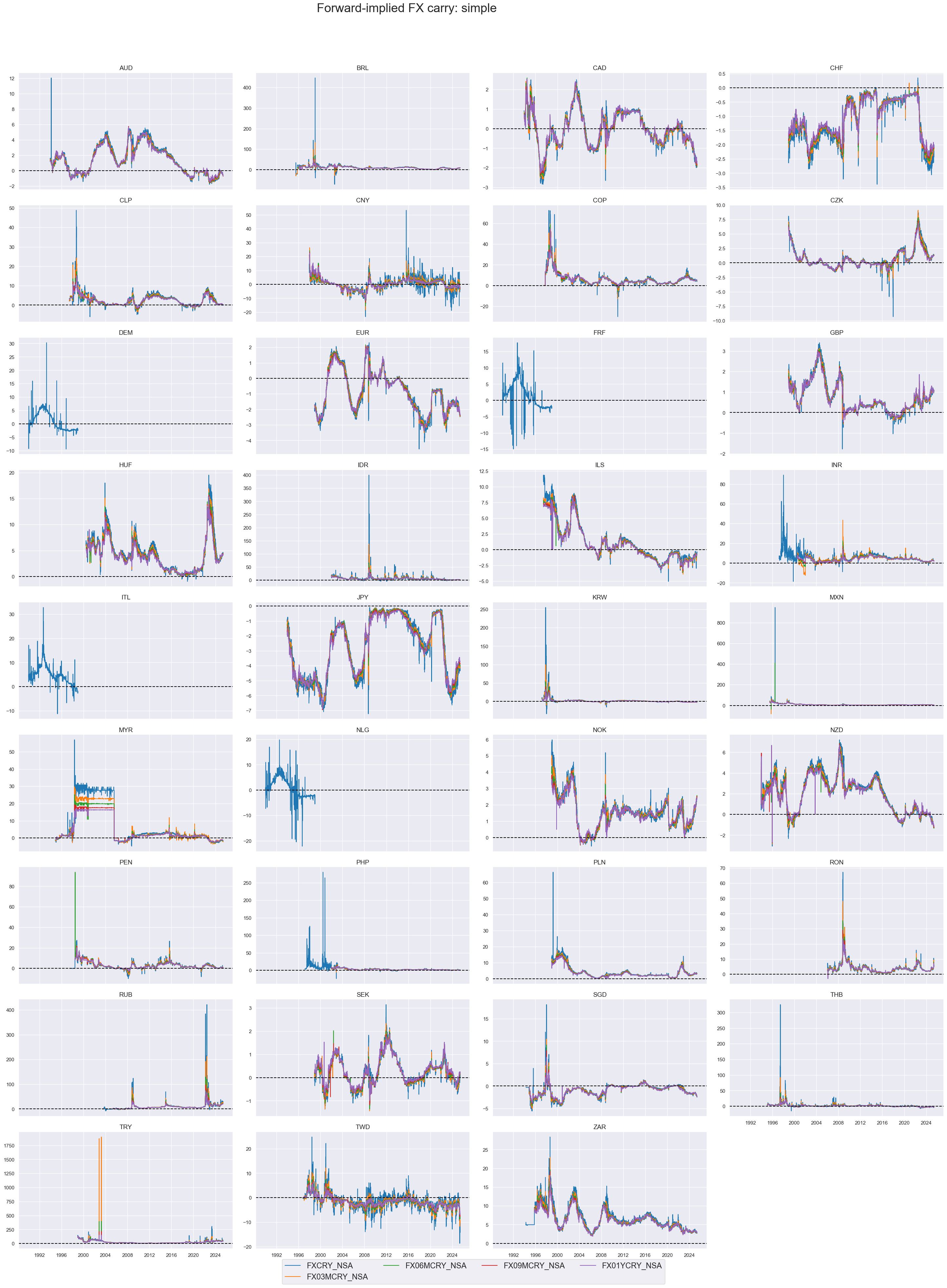
xcatx = [
    "FXCRY_NSA", "FX03MCRY_NSA", "FX06MCRY_NSA", "FX09MCRY_NSA", "FX01YCRY_NSA",
]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start="1990-01-01",
    title="Forward-implied FX carry: simple",
    title_fontsize=27,
    legend_fontsize=17,
    title_adj=1.02,
    title_xadj=0.43,
    cumsum=False,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=False,
)

xcatx = [
    "FXCRY_VT10", "FX03MCRY_VT10", "FX06MCRY_VT10", "FX09MCRY_VT10", "FX01YCRY_VT10",
]
cidx = cids_exp

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
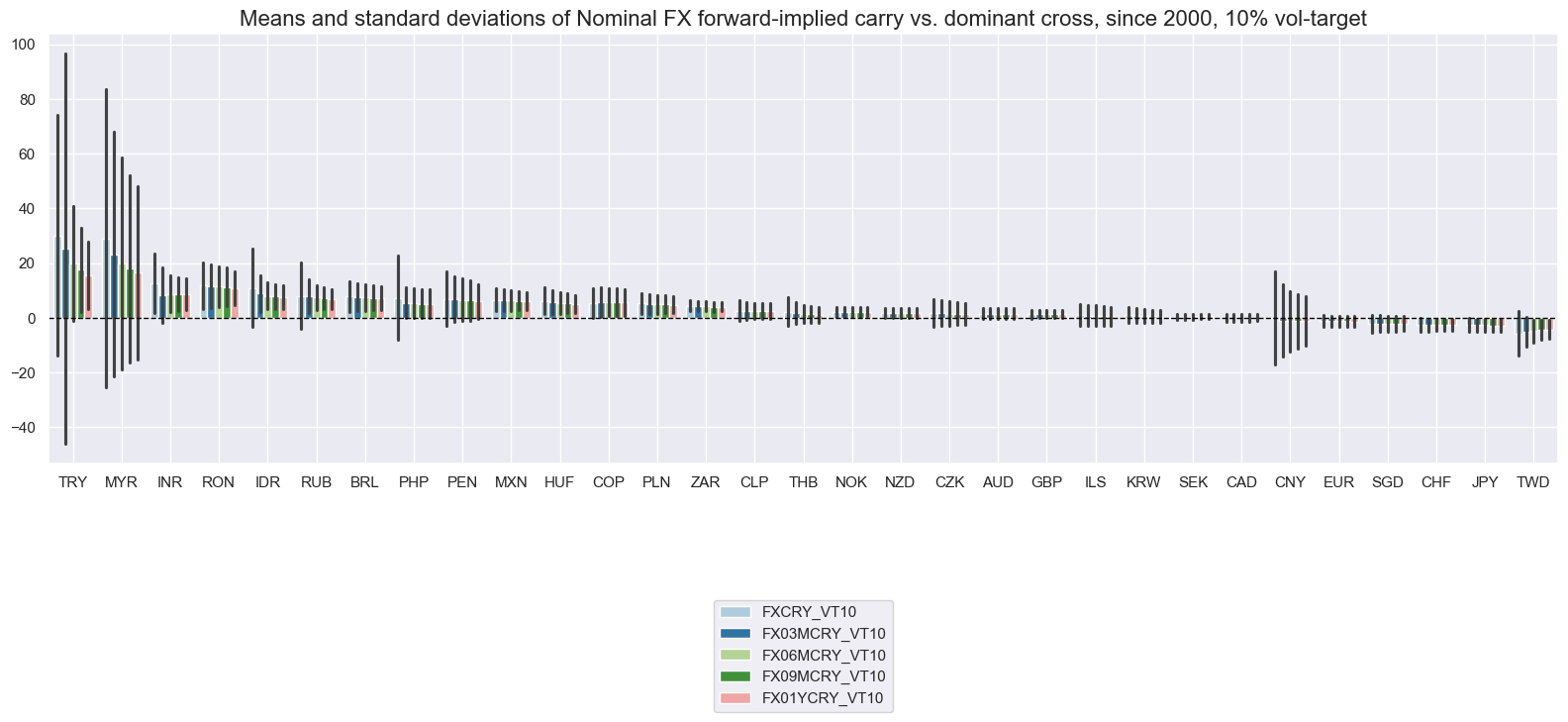
    title="Means and standard deviations of Nominal FX forward-implied carry vs. dominant cross, since 2000, 10% vol-target",
    # xcat_labels=None,
    sort_cids_by="mean",
    start="2000-01-01",
    kind="bar",
    size=(16, 8),
)

xcatx = [
    "FXCRY_VT10", "FX03MCRY_VT10", "FX06MCRY_VT10", "FX09MCRY_VT10", "FX01YCRY_VT10",
]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start="2000-01-01",
    title="Forward-implied FX carry: 10% vol-targeted positions",
    title_fontsize=27,
    legend_fontsize=17,
    title_adj=1.02,
    title_xadj=0.43,
    cumsum=False,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=False,
)

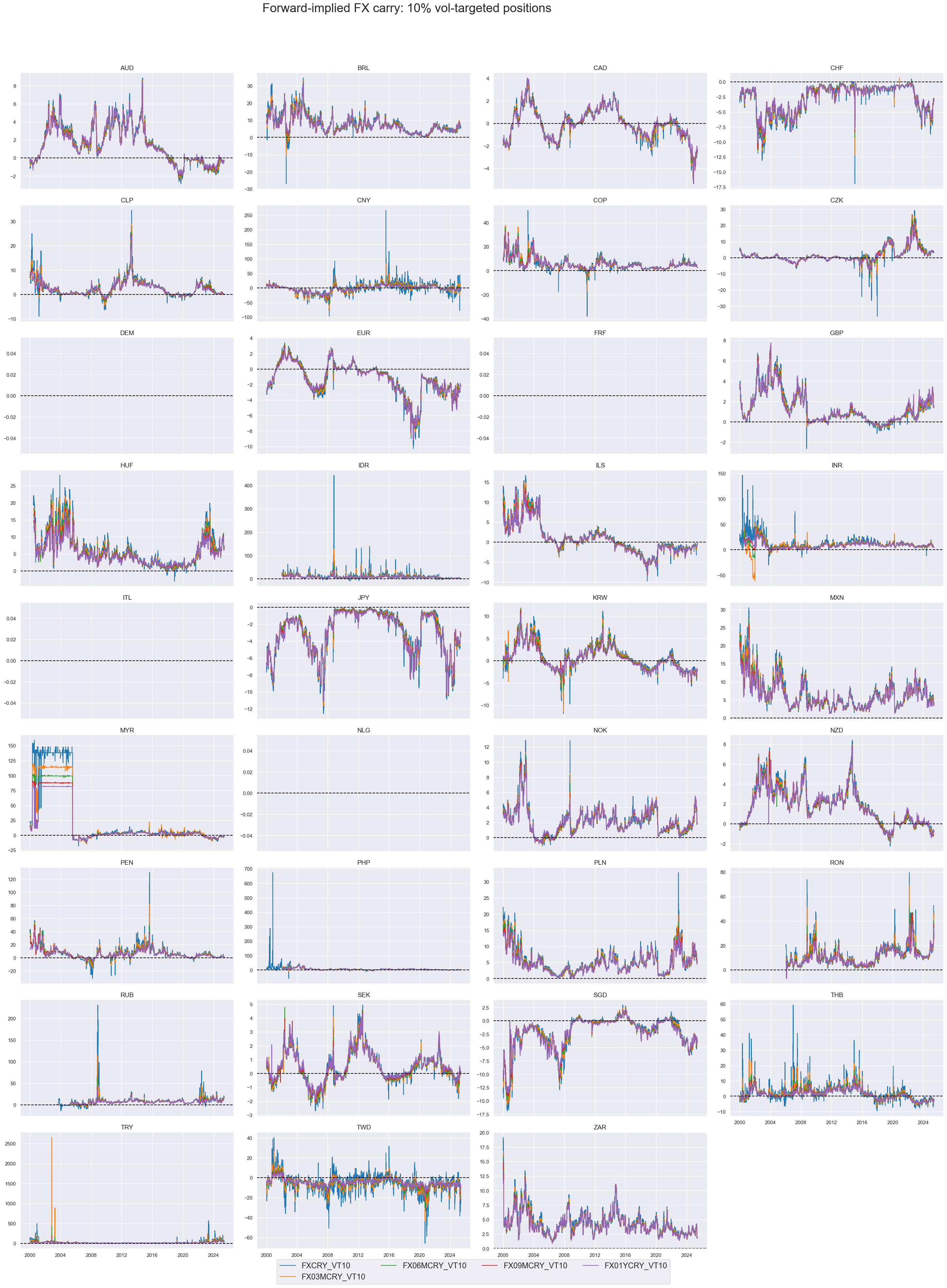
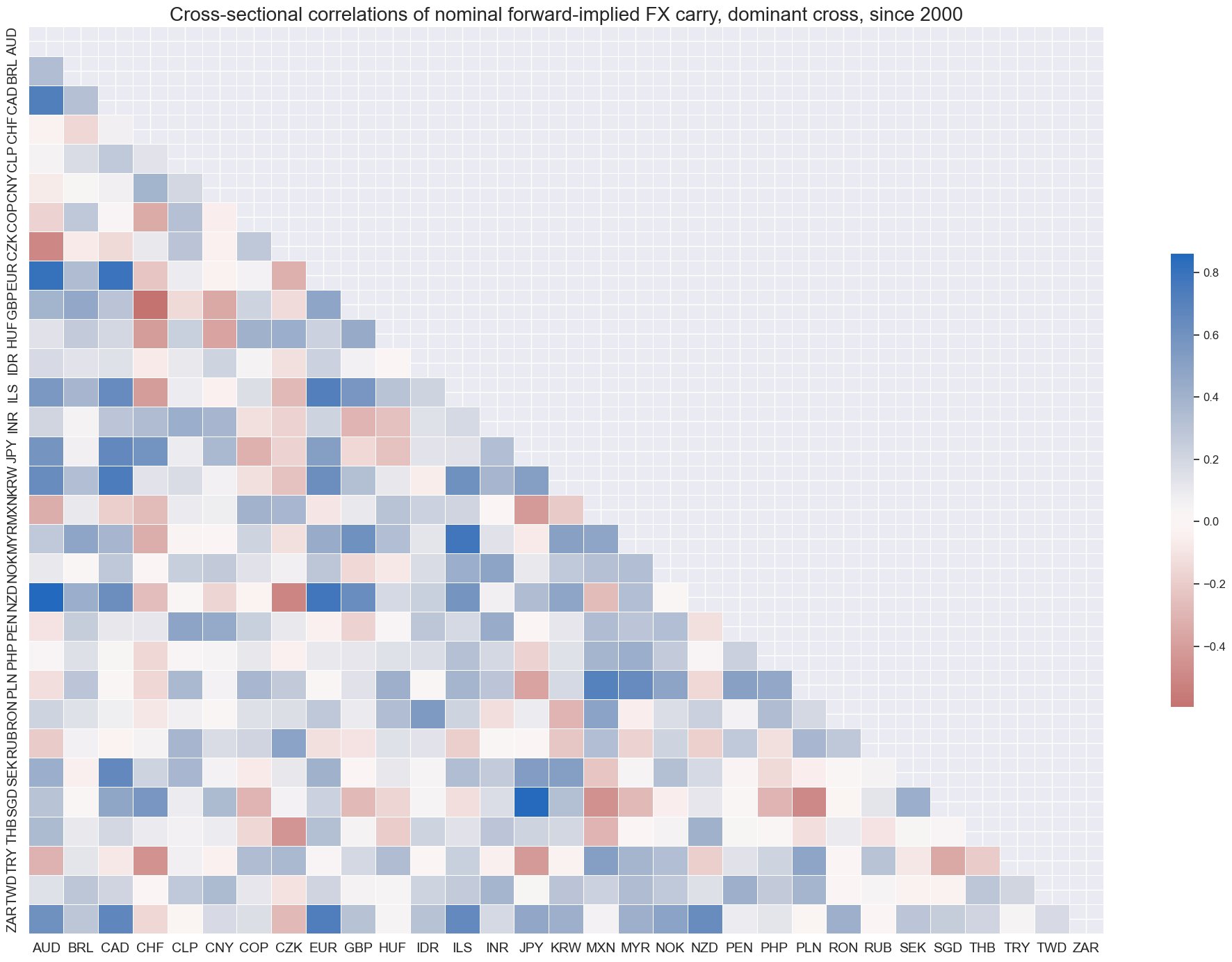
Nominal carry is predominantly positively correlated across currency pairs. That is because most currencies are traded against the same benchmark (USD).

msp.correl_matrix(
    dfd,
    xcats="FXCRY_NSA",
    cids=cids_exp,
    size=(20, 14),
    title="Cross-sectional correlations of nominal forward-implied FX carry, dominant cross, since 2000",
)

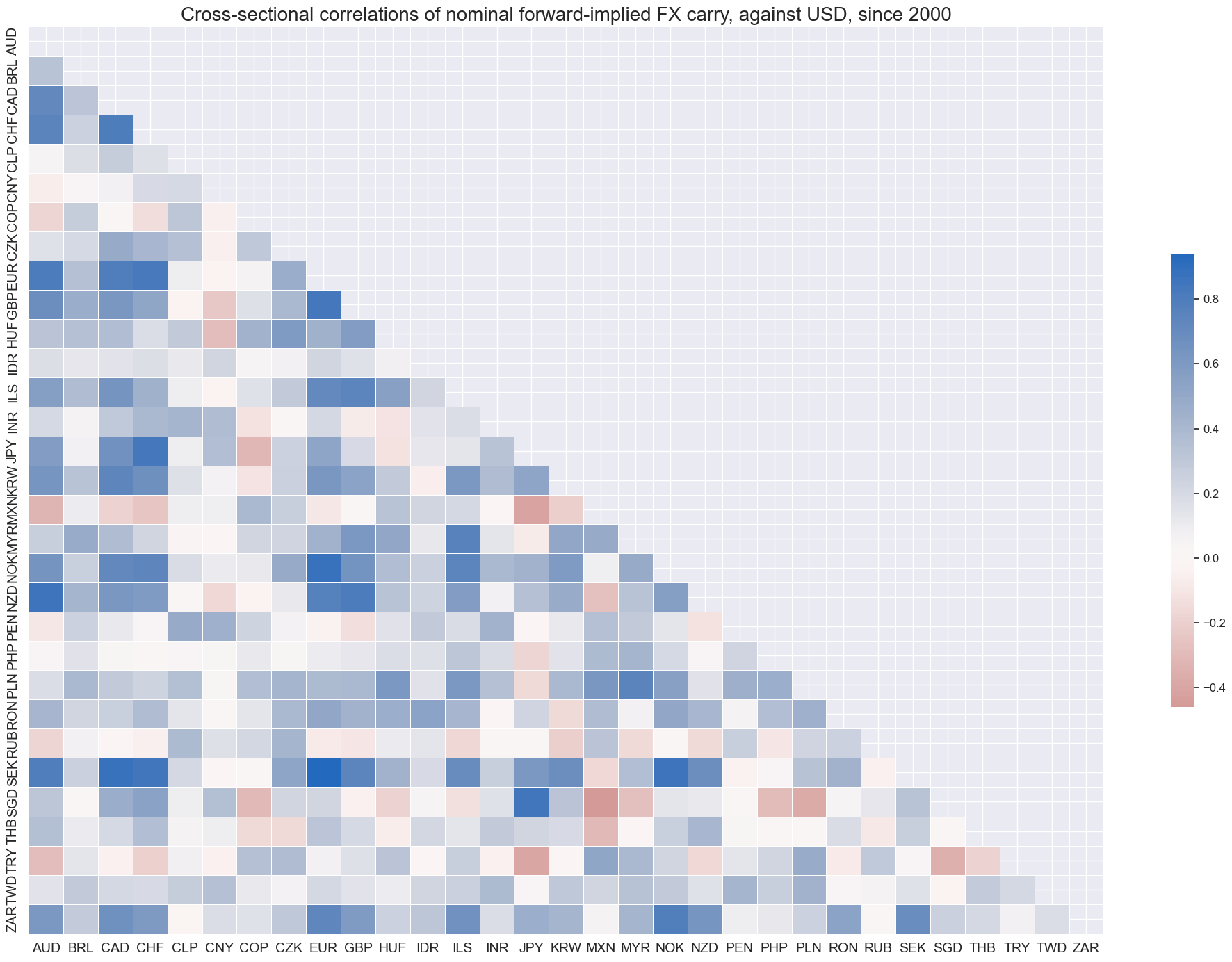
If one looks at USD-based carry alone, global correlation is naturally stronger abut still not uniformly positive for all currencies.

msp.correl_matrix(
    dfd,
    xcats="FXCRYUSD_NSA",
    cids=cids_exp,
    title="Cross-sectional correlations of nominal forward-implied FX carry, against USD, since 2000",
    size=(20, 14),
)

Nominal carry with hedge

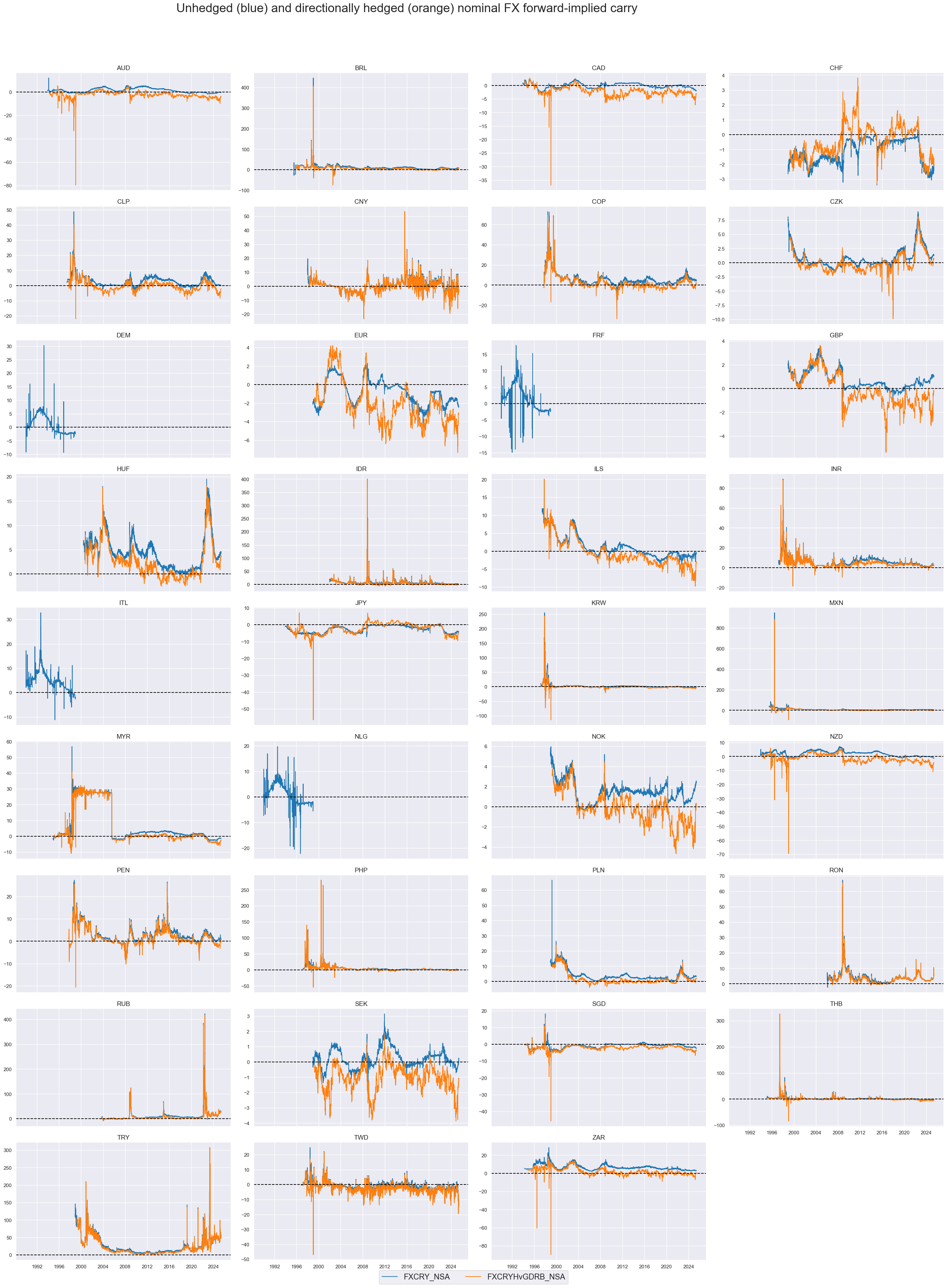
Hedging makes a significant difference for long-term averages and intertemporal dynamics of FX carry positions. Carry for hedged positions has not only been substantially lower for “high-beta” countries, but also a lot more unstable. This is due to the instability of the simple regression estimate of the beta of currency positions with respect to the global directional risk basket.

xcatx = ["FXCRY_NSA", "FXCRYHvGDRB_NSA"]
cidx = cids_exp

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    sort_cids_by="mean",
    start="1990-01-01",
    title="Means and standard deviations of nominal carry on 1-month FX forward positions, since 2000",
    xcat_labels=["Unhedged", "Hedged"],
    kind="bar",
    size=(16, 8),
)

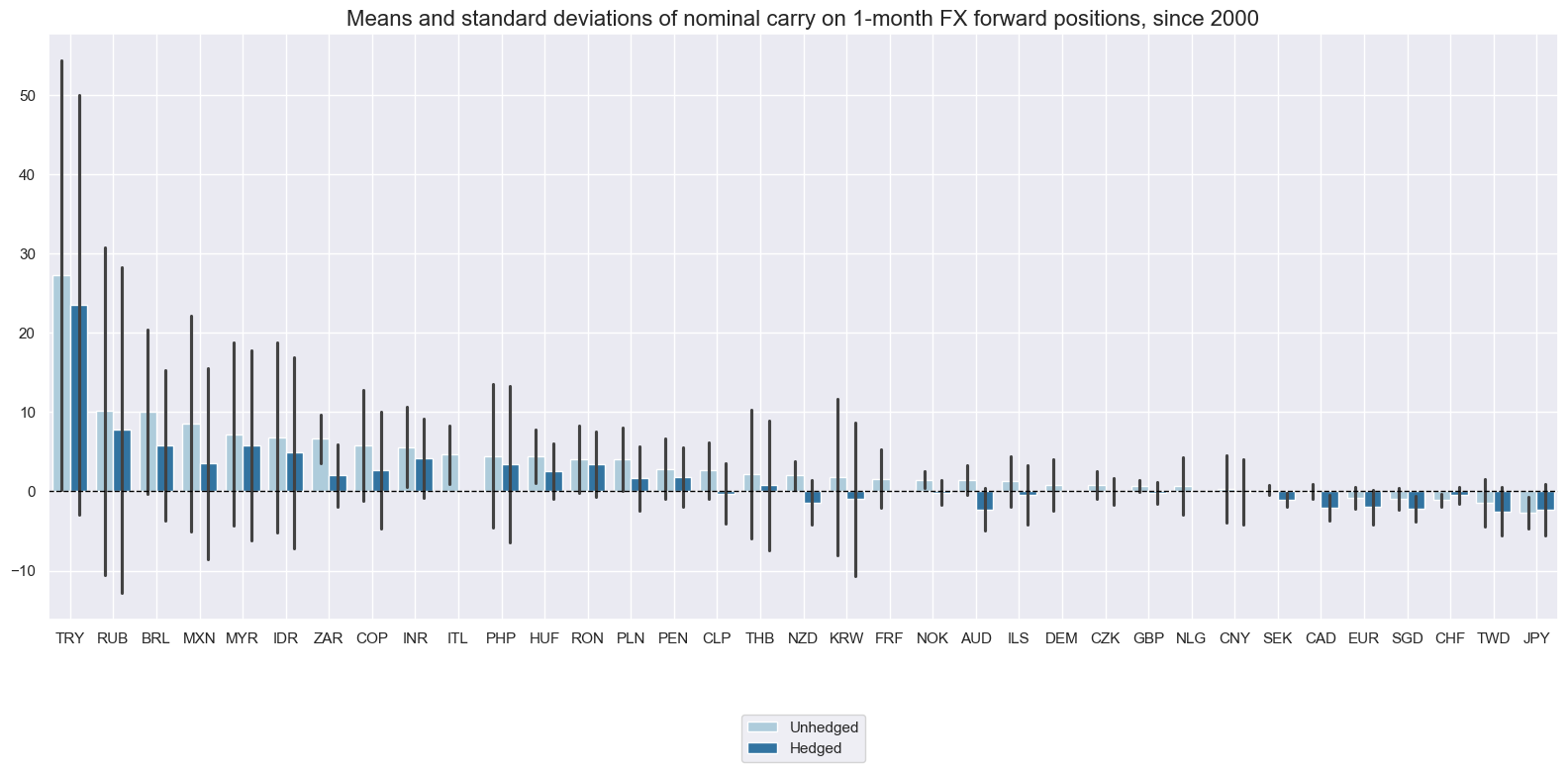
xcatx = ["FXCRY_NSA", "FXCRYHvGDRB_NSA"]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start="1990-01-01",
    title="Unhedged (blue) and directionally hedged (orange) nominal FX forward-implied carry",
    title_adj=1.02,
    title_fontsize=27,
    legend_fontsize=17,
    title_xadj=0.43,
    cumsum=False,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=False,
)

Real carry metrics (no hedges)

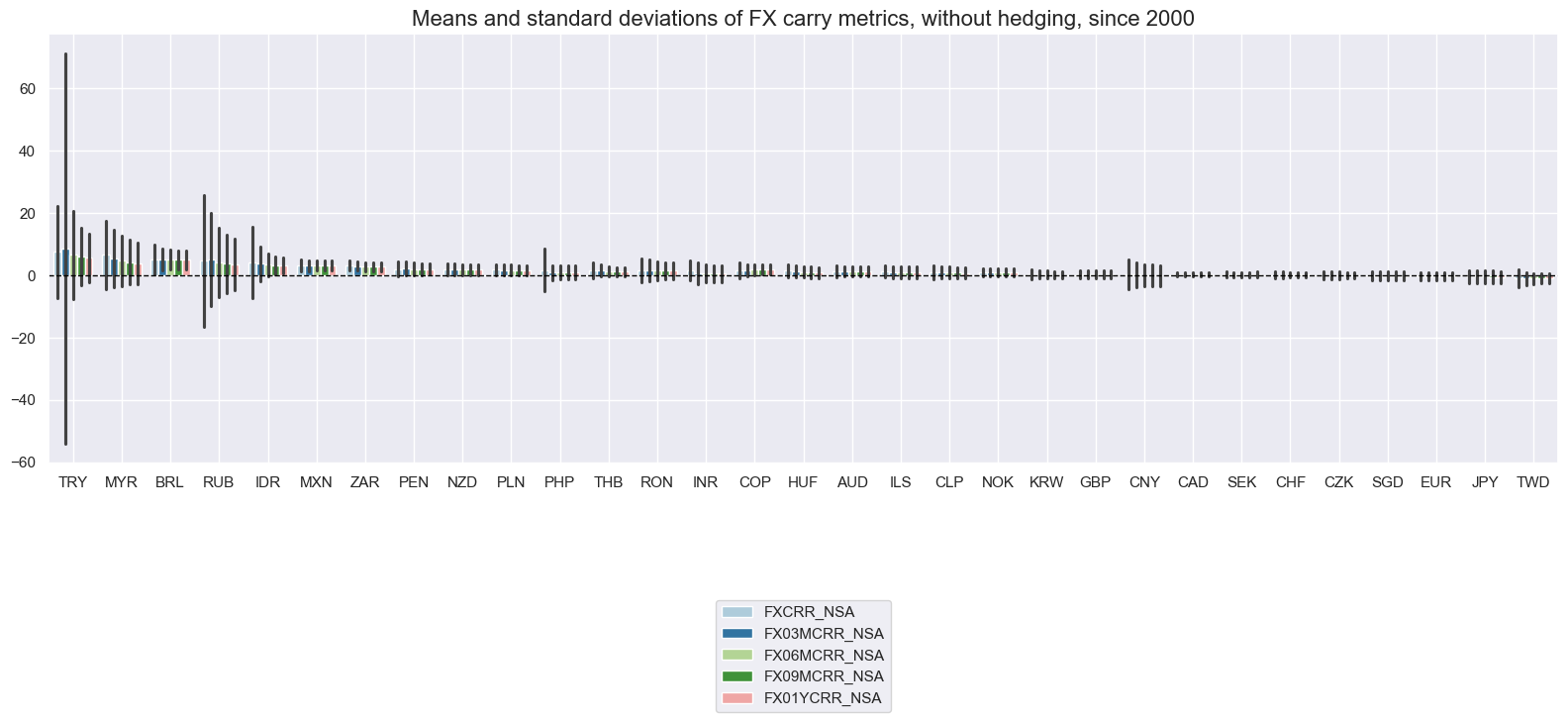
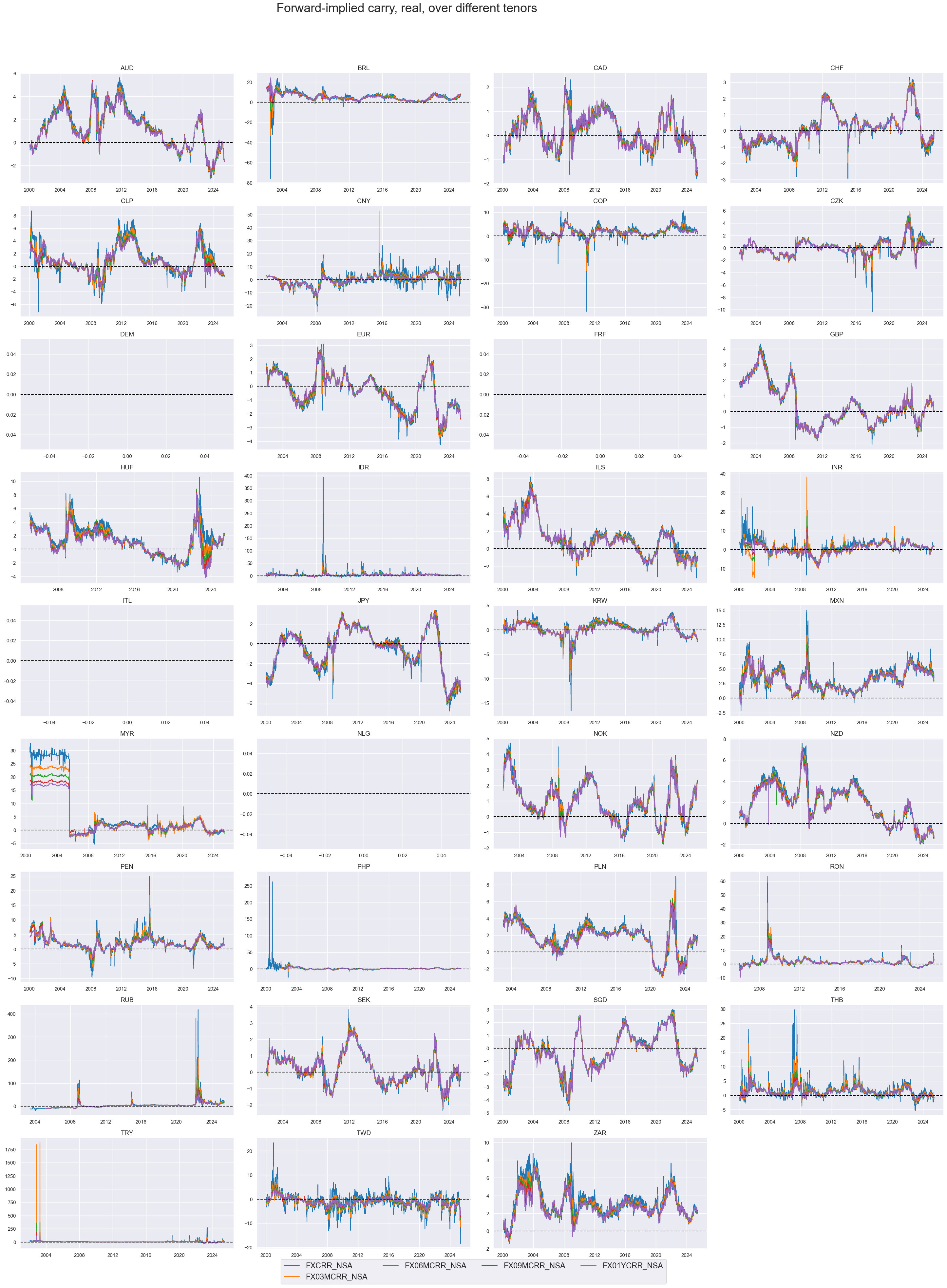
Adjusting FX carry for inflation expectations differentials makes a huge difference for carry-based signals in the long run. This applies to both vol-adjusted and non-vol-adjusted carry. The case for inflation expectation adjustment for measuring actual incentives to hold currency deposits is compelling from a theroetical and empirical perspective.

xcatx = [
    "FXCRR_NSA", "FX03MCRR_NSA", "FX06MCRR_NSA", "FX09MCRR_NSA", "FX01YCRR_NSA",
]
cidx = cids_exp

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    sort_cids_by="mean",
    start="2000-01-01",
    title="Means and standard deviations of FX carry metrics, without hedging, since 2000",
    # xcat_labels=["Real", "Nominal"],
    kind="bar",
    size=(16, 8),
)

xcatx = [
    "FXCRR_NSA", "FX03MCRR_NSA", "FX06MCRR_NSA", "FX09MCRR_NSA", "FX01YCRR_NSA",
    ]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start="2000-01-01",
    title="Forward-implied carry, real, over different tenors",
    # xcat_labels=["Real", "Nominal"],
    title_adj=1.02,
    title_fontsize=27,
    legend_fontsize=17,
    title_xadj=0.43,
    cumsum=False,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=True,
)

xcatx = [
    "FXCRR_VT10", "FX03MCRR_VT10", "FX06MCRR_VT10", "FX09MCRR_VT10", "FX01YCRR_VT10",
]
cidx = cids_exp

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    sort_cids_by="mean",
    start="2000-01-01",
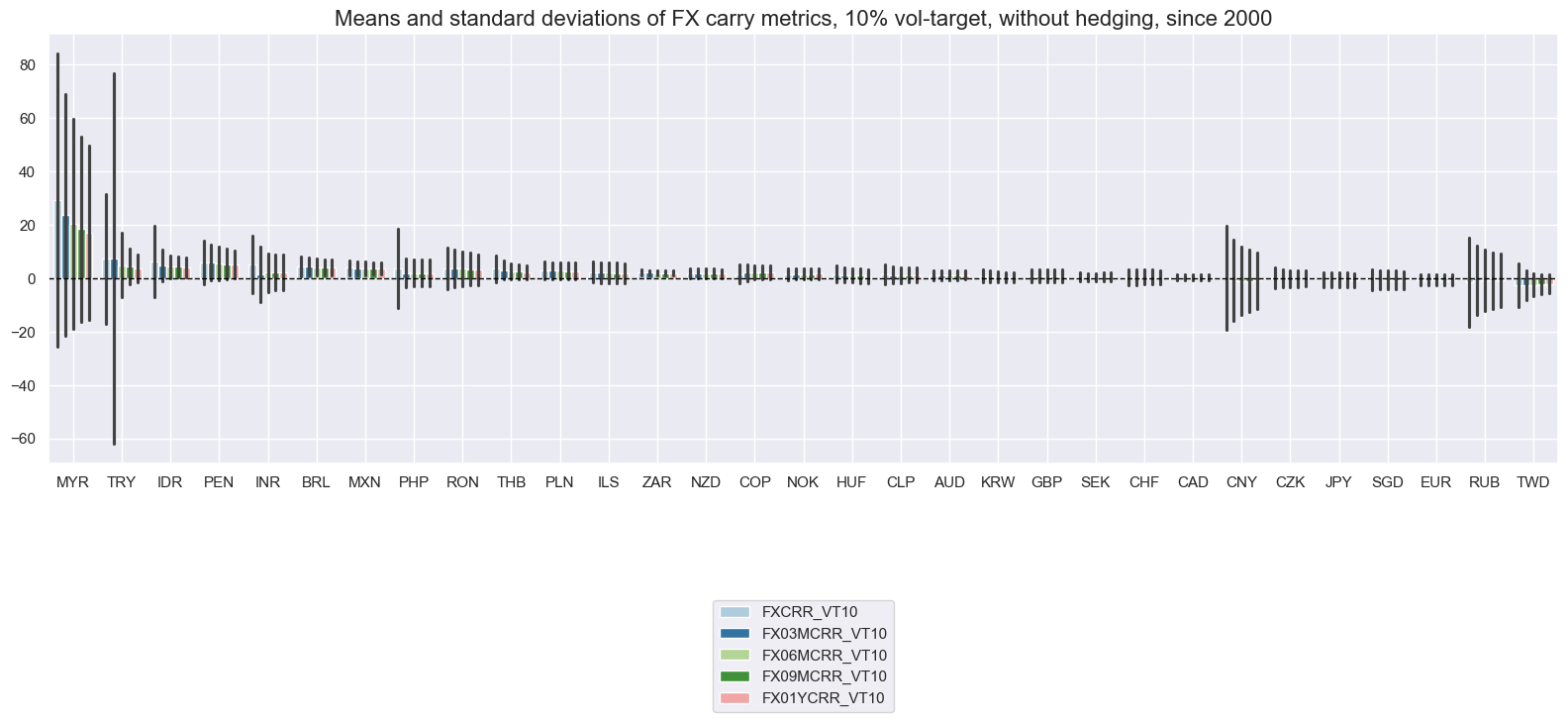
    title="Means and standard deviations of FX carry metrics, 10% vol-target, without hedging, since 2000",
    # xcat_labels=["Real", "Nominal"],
    kind="bar",
    size=(16, 8),
)

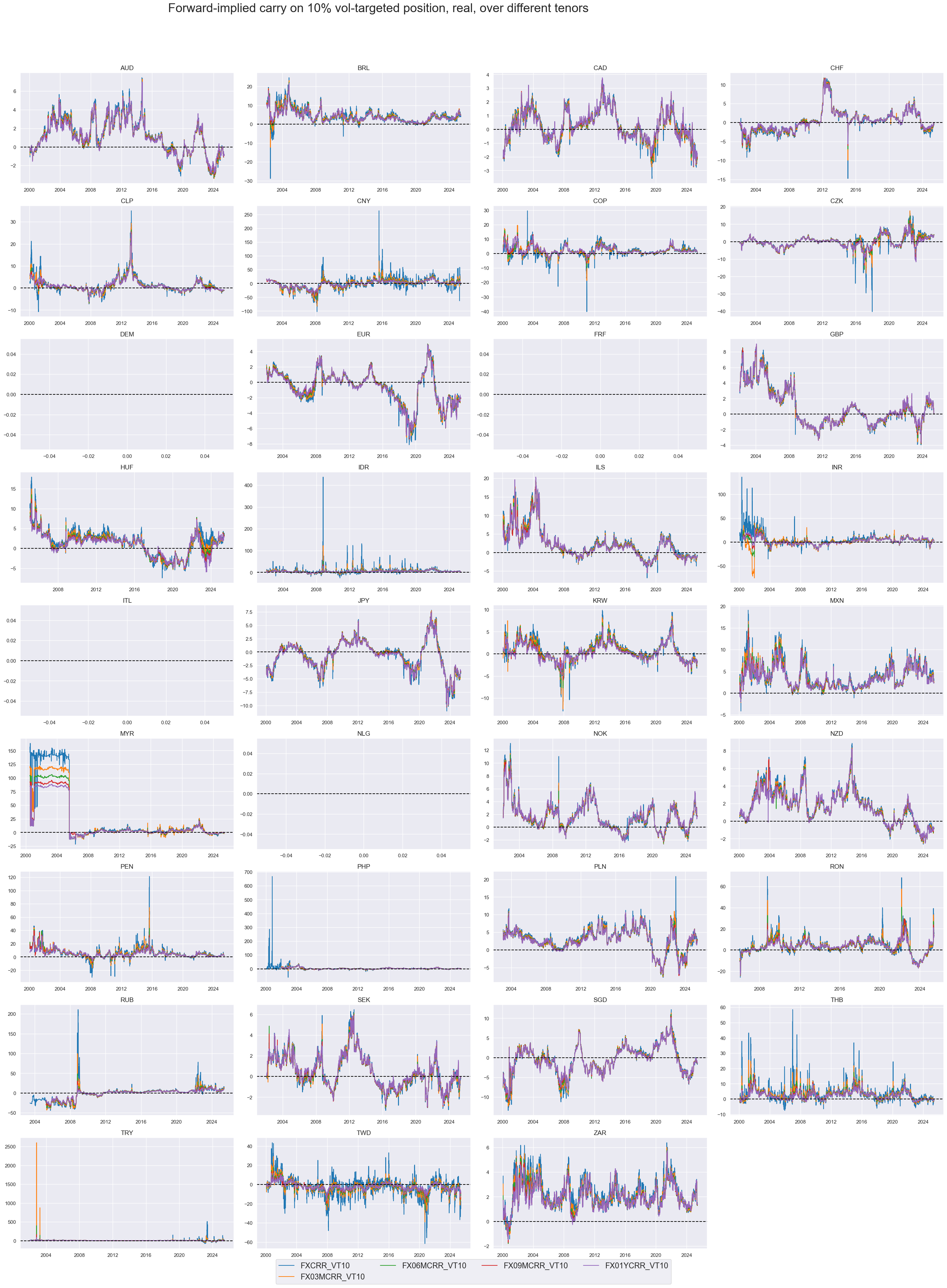
xcatx = [
    "FXCRR_VT10", "FX03MCRR_VT10", "FX06MCRR_VT10", "FX09MCRR_VT10", "FX01YCRR_VT10",
]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start="2000-01-01",
    title="Forward-implied carry on 10% vol-targeted position, real, over different tenors",
    # xcat_labels=["Real", "Nominal"],
    title_adj=1.02,
    title_fontsize=27,
    legend_fontsize=17,
    title_xadj=0.4,
    cumsum=False,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=True,
)

Real carry with hedge

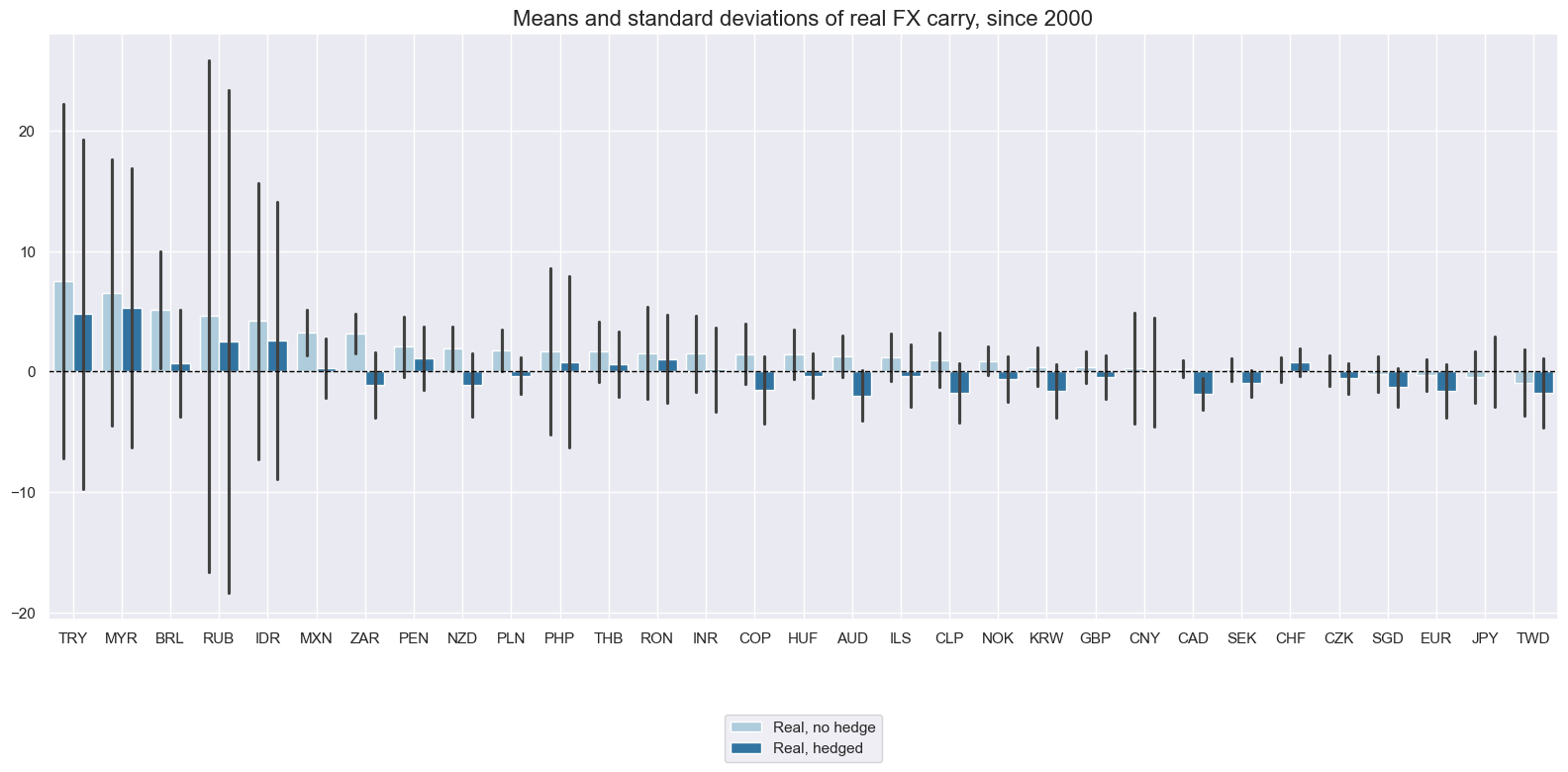
As for nominal carry, hedging makes a significant difference for long-term averages and intertemporal dynamics of real carry. Several currencies have displayed positive real carry without a directional hedge but negative real carry with a directional hedge. This illustrates that FX-specific carry does not always sufficiently compensate for the borader market “beta” of a currency.

xcatx = ["FXCRR_NSA", "FXCRRHvGDRB_NSA"]
cidx = cids_exp

msp.view_ranges(
    dfd,
    xcats=xcatx,
    cids=cidx,
    sort_cids_by="mean",
    start="2000-01-01",
    title="Means and standard deviations of real FX carry, since 2000",
    xcat_labels=["Real, no hedge", "Real, hedged"],
    kind="bar",
    size=(16, 8),
)

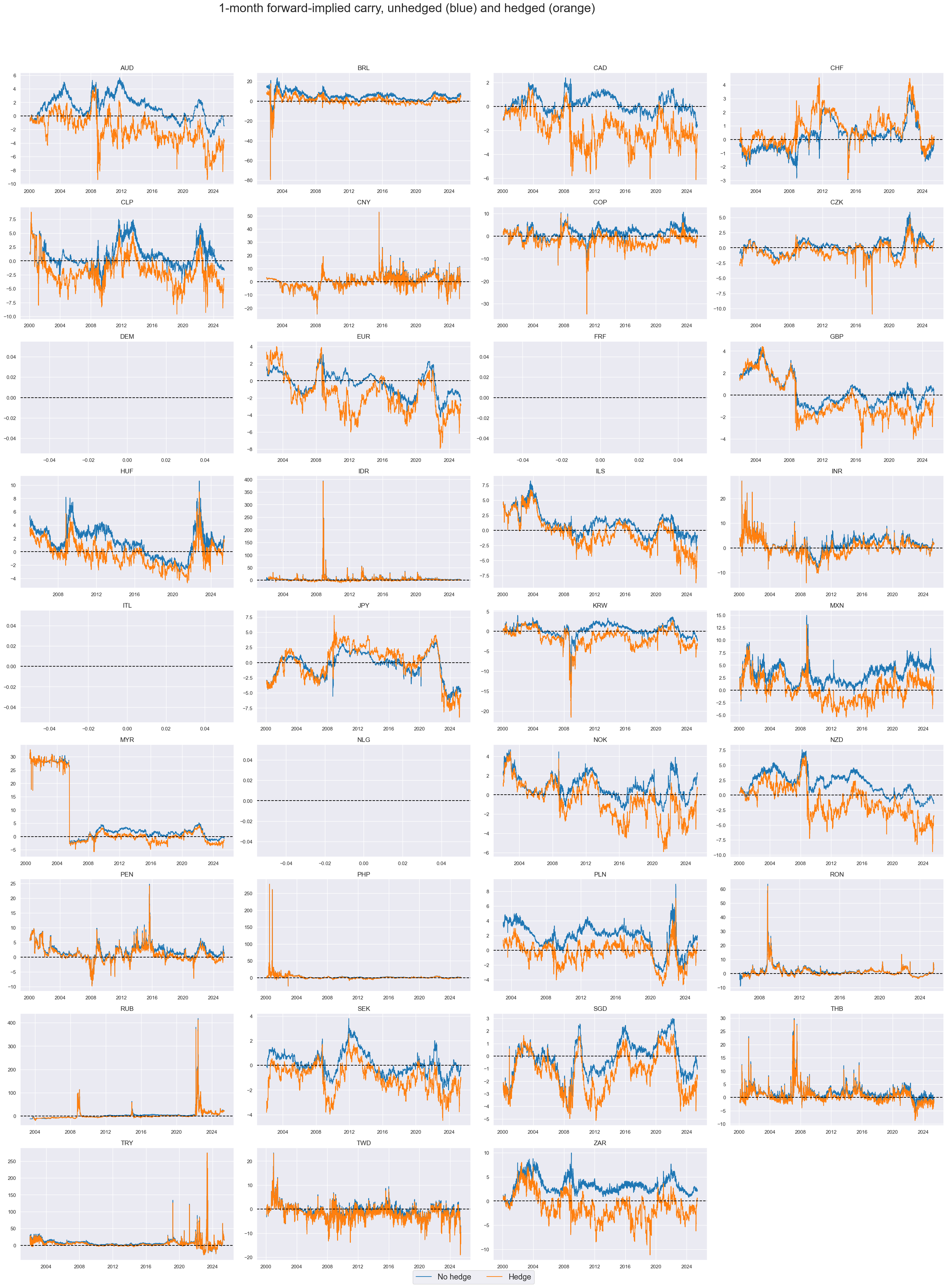
xcatx = ["FXCRR_NSA", "FXCRRHvGDRB_NSA"]
cidx = cids_exp

msp.view_timelines(
    dfd,
    xcats=xcatx,
    cids=cidx,
    start="2000-01-01",
    title="1-month forward-implied carry, unhedged (blue) and hedged (orange)",
    xcat_labels=["No hedge", "Hedge"],
    title_adj=1.02,
    title_fontsize=27,
    legend_fontsize=17,
    title_xadj=0.43,
    cumsum=False,
    ncol=4,
    same_y=False,
    size=(12, 7),
    aspect=1.7,
    all_xticks=True,
)

Importance

Research links

“On a granular basis, nominal carry has tended to perform better for G10 while real yields have been a better signal for EM particularly in recent years…we find that the returns from using the current account balance as signals are negatively correlated with returns from FX carry.” See Chandan and Duran-Vara , and Chandan et al

“Simply a combination of two factors—carry and growth or carry and external balances—is adequate to deliver risk-adjusted returns of near one. Meanwhile, any two-factor combination that includes value underperforms.” See Chandan and Chandan and Duran-Vara .

“It has thus become substantially less onerous to be short high beta currencies, thus resulting in their emergence as viable risk market hedges.” Chandan

“Although ’naive’ returns to the FX carry trade, as documented elsewhere in the literature are strongly positive, allowing for stop-loss rules results in returns that are insignificantly different from zero. The ability to cash in on the much vaunted forward premium puzzle relies on being able to stay in the trade, which seems strongly at odds with industry risk management policies.” Carrodus

“The predictive capacity of forward discounts on future currency returns not only differs across currencies but also persists.” Choi and Suh

“FX forward-implied carry is a valid basis for investment strategies because it is related to policy subsidies and risk premia. However, it also contains misdirection such as rational expectations of currency depreciation. To increase the signal-noise ratio FX carry should – at the very least – be adjusted for expected inflation differentials.” Macrosynergy

“There is often a strong case for hedging FX carry trades against unrelated global market factors. It is usually not difficult to hedge currency positions – at least partly – against global directional risk and against moves in the EURUSD exchange rate. The benefits of these hedges are [1] more idiosyncratic and diversifiable currency trades and, [2] a more realistic assessment of the actual currency-specific subsidy or risk premium implied by carry, by applying hedge costs to the carry measure. Empirical analysis suggests that regression-based hedging improves Sharpe ratios, reduces risk correlation and removes downside skews in the returns of global FX carry strategies. Hedging works well in conjunction with “economically adjusted” FX carry and even benefits the performance of relative FX carry strategies that have no systematic risk correlation to begin with.” Macrosynergy

Empirical clues

One of the most salient stylized features of past decades has been a long-term positive relation between real (inflation expectations-adjusted) forward-implied carry and FX forward returns.

# Blacklist dictionary for invalid periods across currency areas since 2000.

dfb = dfd[dfd["xcat"].isin(["FXTARGETED_NSA", "FXUNTRADABLE_NSA"])].loc[
    :, ["cid", "xcat", "real_date", "value"]
]
dfba = (
    dfb.groupby(["cid", "real_date"])
    .aggregate(value=pd.NamedAgg(column="value", aggfunc="max"))
    .reset_index()
)
dfba["xcat"] = "FXBLACK"
fxblack = msp.make_blacklist(dfba, "FXBLACK")

xcatx = ["FXCRR_NSA", "FXXR_NSA"]
cidx = cids_exp

cr = msp.CategoryRelations(
    dfd,
    xcats=xcatx,
    cids=cidx,
    freq="A",
    lag=0,
    xcat_aggs=["mean", "sum"],
    blacklist=fxblack,
    start="2000-01-01",
    years=None,
)

cr.reg_scatter(
    title="FX real implied carry and contemporaneous returns across all countries and years since 2000",
    labels=True,
    coef_box="lower right",
    xlab="Real FX forward-implied carry, % ar",
    ylab="Cumulative 1-year return",
)

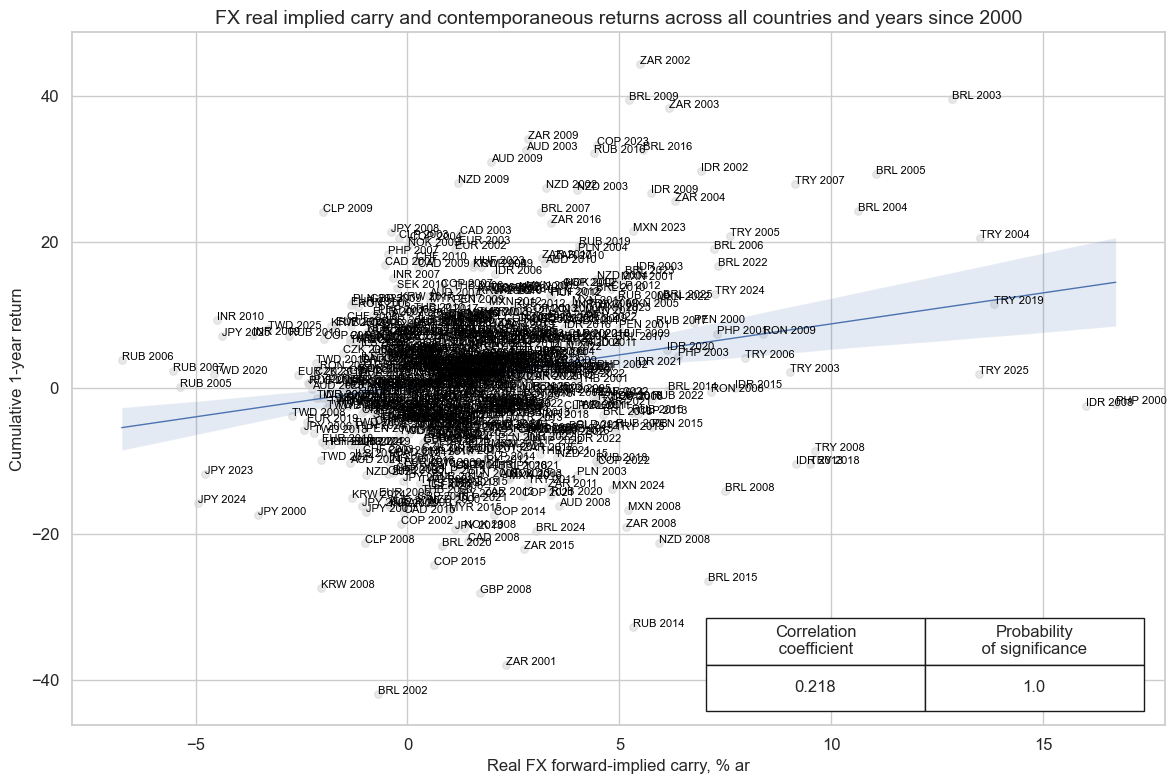
Real carry has also historically predicted subsequent monthly and quarterly FX forward returns with very high probability of significance. The relation held true for both the early and later half of the sample period since 2000.

xcatx = ["FXCRR_NSA", "FXXR_NSA"]
cidx = cids_exp

cr = msp.CategoryRelations(
    dfd,
    xcats=xcatx,
    cids=cidx,
    freq="M",
    lag=1,
    xcat_aggs=["mean", "sum"],
    blacklist=fxblack,
    start=start_date,
    xcat_trims=[50, 50],  # de-emphasize outliers
    years=None,
)

cr.reg_scatter(
    title="FX real implied carry and subsequent returns, all countries since 2000",
    labels=False,
    separator=2012,
    coef_box="lower right",
    xlab="Real FX forward-implied carry, % ar, month average, versus dominant benchmark currency",
    ylab="Next month's 1-month FX forward return",
)

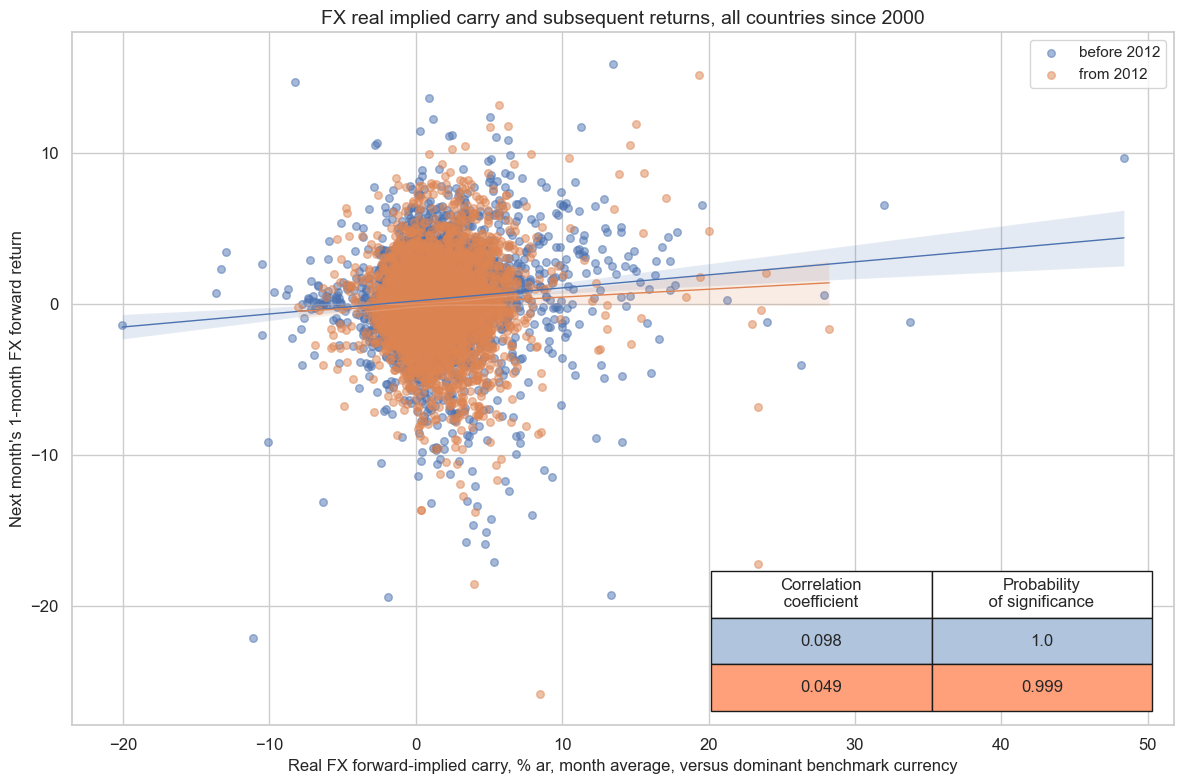
The positive relation between real carry and returns has also prevailed for the longer tenors. However, the longer the tenor, smaller has been the correlation coefficient.

cidx = cids_exp

tenor_names = {
    "3M": "3-months", 
    "6M": "6-months", 
    "9M": "9-months", 
    "1Y": "12-months"
}

carry_ret_cr = {}
for tenor in ["3M", "6M", "9M", "1Y"]:
    carry_ret_cr[tenor] = msp.CategoryRelations(
        dfd,
        xcats=[f"FX0{tenor}CRR_NSA", f"FX0{tenor}XR_NSA"],
        cids=cidx,
        freq="M",
        lag=1,
        xcat_aggs=["mean", "sum"],
        blacklist=fxblack,
        start="2000-01-01",
        years=None,
    )

msv.multiple_reg_scatter(
        carry_ret_cr.values(),
        title="FX forwards for various tenors: real carry and subsequent returns, all EM/DM currencies since 2000",
        ylab="% return, next month",
        ncol=2,
        nrow=2,
        figsize=(16, 12),
        prob_est="map",
        coef_box="lower left", 
        subplot_titles=[tenor_names.get(k) for k in carry_ret_cr.keys()],
     )

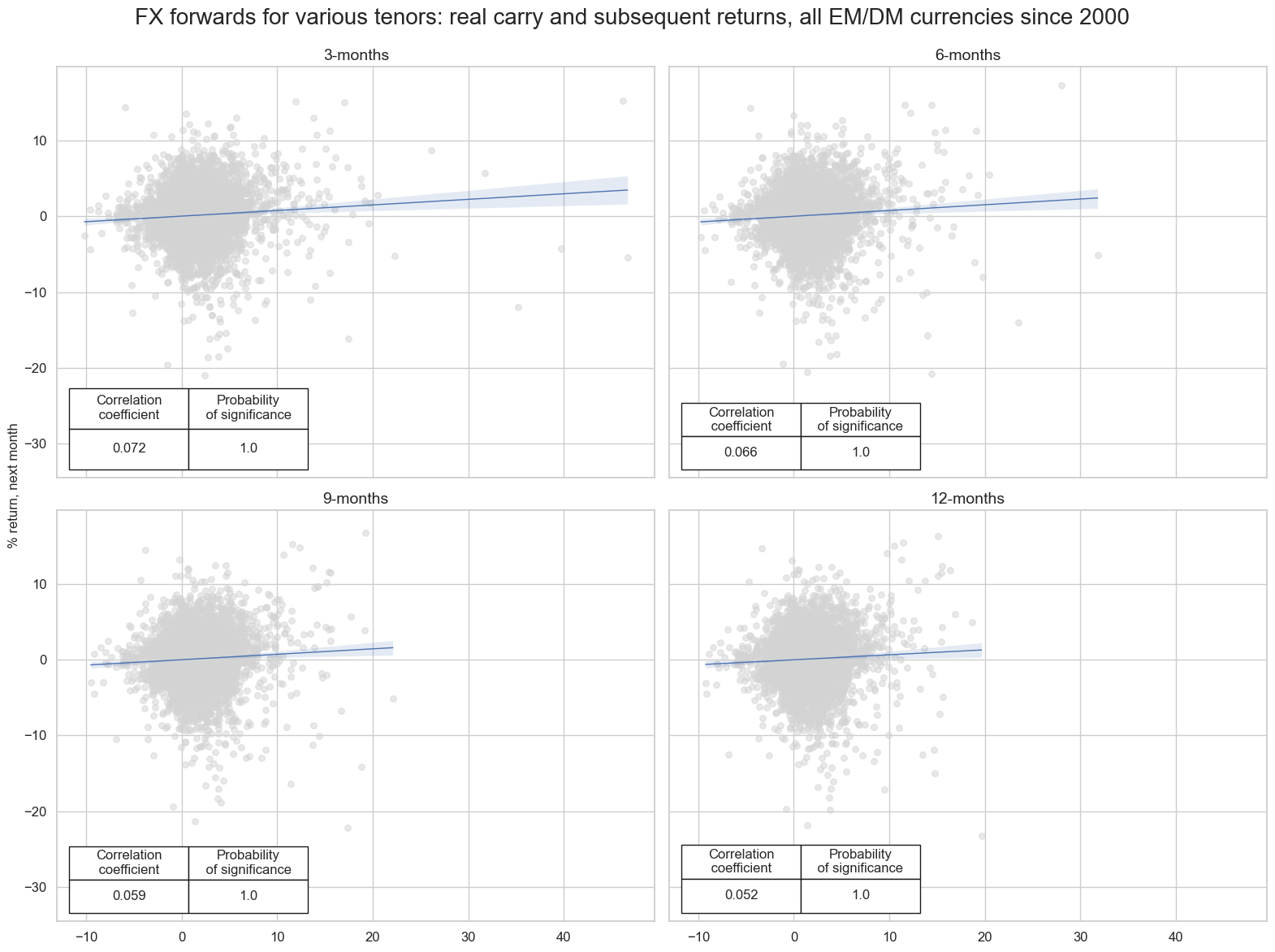
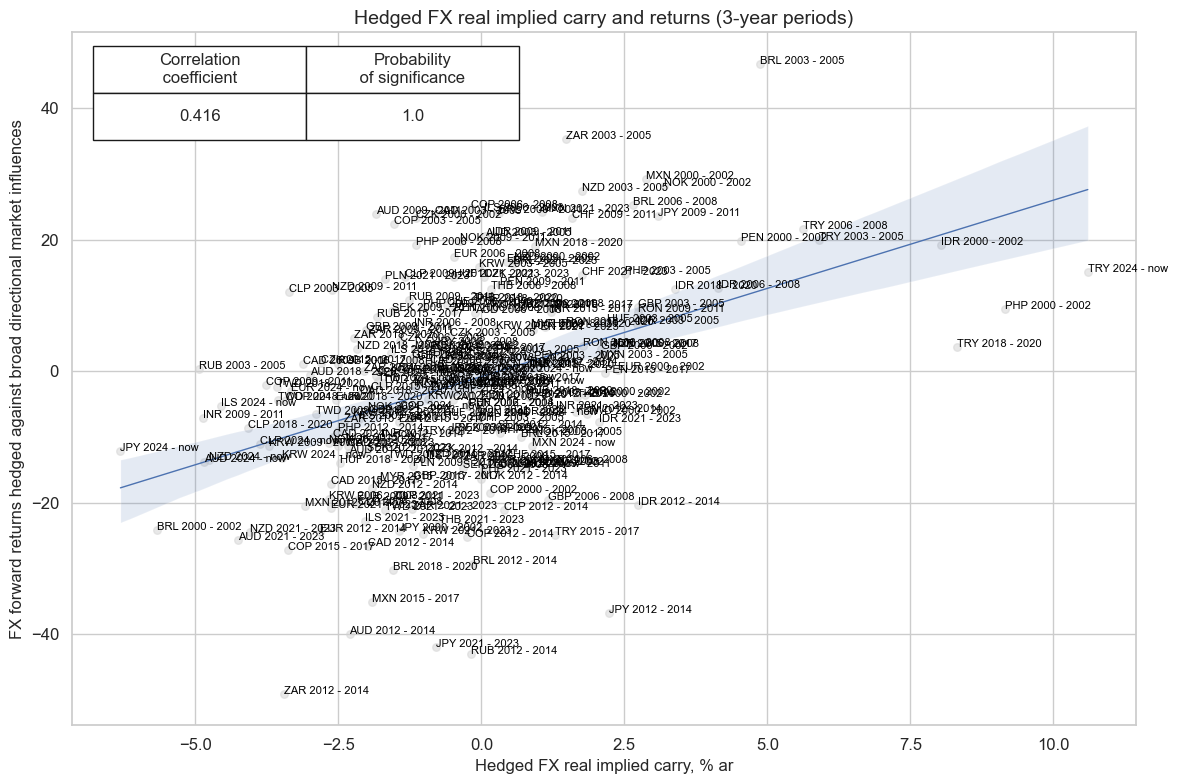
All versions of real carry have been positively correlated with FX forwrad returns over longer horizons

xcatx = ["FXCRRHvGDRB_NSA", "FXXRHvGDRB_NSA"]
cidx = cids_exp
cr = msp.CategoryRelations(
    dfd,
    xcats=xcatx,
    cids=cidx,
    freq="M",
    lag=0,
    xcat_aggs=["mean", "sum"],
    blacklist=fxblack,
    start="2000-01-01",
    years=3,
)
cr.reg_scatter(
    title="Hedged FX real implied carry and returns (3-year periods)",
    labels=True,
    coef_box="upper left",
    xlab="Hedged FX real implied carry, % ar",
    ylab="FX forward returns hedged against broad directional market influences",
)

Appendices

Appendix 1: Currency symbols

The word ‘cross-section’ refers to currencies, currency areas or economic areas. In alphabetical order, these are AUD (Australian dollar), BRL (Brazilian real), CAD (Canadian dollar), CHF (Swiss franc), CLP (Chilean peso), CNY (Chinese yuan renminbi), COP (Colombian peso), CZK (Czech Republic koruna), DEM (German mark), ESP (Spanish peseta), EUR (Euro), FRF (French franc), GBP (British pound), HKD (Hong Kong dollar), HUF (Hungarian forint), IDR (Indonesian rupiah), ITL (Italian lira), JPY (Japanese yen), KRW (Korean won), MXN (Mexican peso), MYR (Malaysian ringgit), NLG (Dutch guilder), NOK (Norwegian krone), NZD (New Zealand dollar), PEN (Peruvian sol), PHP (Phillipine peso), PLN (Polish zloty), RON (Romanian leu), RUB (Russian ruble), SEK (Swedish krona), SGD (Singaporean dollar), THB (Thai baht), TRY (Turkish lira), TWD (Taiwanese dollar), USD (U.S. dollar), ZAR (South African rand).

Appendix 2: FX forward day count convention and spot settlement

To calculate the number of days in an FX forward contract, we take into account holidays in both currency regions, the applicable day count conventions, and the number of days between the spot date and the settlement date. For example, consider a 1-month (1M) FX forward contract for AUD/USD traded on 1 July 2022:

1. Trade Date: 1 July 2022 (Friday)

2. Spot Date: 6 July 2022 (Wednesday) - the standard FX spot convention is T+2, but intervening non-business days (2–3 July weekend, 4 July U.S. holiday) push the spot date to 6 July.

3. Settlement Date: 8 August 2022 (Monday) - adding one calendar month to the spot date gives 6 August 2022, which falls on a Saturday. The date is adjusted forward to the next business day, which is 8 August.

The number of days in the FX forward contract is: 8 August 2022 – 6 July 2022 = 33 days

To express this as a year fraction, we use each currency’s day count convention:

1. AUD (Actual/365): 33 / 365

2. USD (Actual/360): 33 / 360

# FX convention data
data = [
     ("AUD", "A/365", 2),
    ("CAD", "A/365", 1),
    ("CHF", "A/360", 2),
    ("EUR", "A/360", 2),
    ("GBP", "A/365", 2),
    ("JPY", "A/360", 2),
    ("NOK", "A/360", 2),
    ("NZD", "A/365", 2),
    ("SEK", "A/360", 2),
    ("USD", "A/360", 2),
    ("BRL", "BD/252", 2),
    ("COP", "A/360", 2),
    ("CLP", "A/360", 2),
    ("MXN", "A/360", 2),
    ("PEN", "A/360", 2),
    ("CZK", "A/360", 2),
    ("HUF", "A/360", 2),
    ("ILS", "A/365", 2),
    ("PLN", "A/365", 2),
    ("RON", "A/360", 2),
    ("RUB", "A/365", 1),
    ("TRY", "A/360", 1),
    ("ZAR", "A/365", 2),
    ("CNY", "A/365", 2),
    ("IDR", "A/365", 2),
    ("INR", "A/365", 2),
    ("KRW", "A/365", 2),
    ("MYR", "A/365", 2),
    ("PHP", "A/365", 2),
    ("SGD", "A/365", 2),
    ("THB", "A/365", 2),
    ("TWD", "A/365", 2),
]


# Create DataFrame
table = pd.DataFrame(data, columns=["Currency", "FX forward day count convention", "FX Spot Settlement"])
table = table.sort_values(by="Currency")

# Display without index
from IPython.display import display, HTML
display(HTML(table.to_html(index=False)))

Currency	FX forward day count convention	FX Spot Settlement
AUD	A/365	2
BRL	BD/252	2
CAD	A/365	1
CHF	A/360	2
CLP	A/360	2
CNY	A/365	2
COP	A/360	2
CZK	A/360	2
EUR	A/360	2
GBP	A/365	2
HUF	A/360	2
IDR	A/365	2
ILS	A/365	2
INR	A/365	2
JPY	A/360	2
KRW	A/365	2
MXN	A/360	2
MYR	A/365	2
NOK	A/360	2
NZD	A/365	2
PEN	A/360	2
PHP	A/365	2
PLN	A/365	2
RON	A/360	2
RUB	A/365	1
SEK	A/360	2
SGD	A/365	2
THB	A/365	2
TRY	A/360	1
TWD	A/365	2
USD	A/360	2
ZAR	A/365	2

Appendix 3: the BRL implied yield

Following the BRL local swap (DI) market convention, we estimate the implied yield using exponential interpolation instead of linear interpolation:

(5) \[\begin{equation} \hat{i}_{\text{BRL}} = 100 \cdot \left\{ \left[ \left( \frac{S_{\text{BRL/USD}}}{F_{\text{BRL/USD}}} \right) \cdot \left( 1 + i_{\text{USD}} \cdot \frac{h_{USD}}{100} \right) \right]^{\left( \frac{1}{h_{BRL}} \right)} - 1 \right\} \end{equation}\]

Where \(S_{\text{BRL}/\text{USD}}\) is the spot price, \(F_{\text{BRL}/\text{USD}}\) is the forward contract, \(i_{USD}\) is the US interest rate taken as the mid-market swap yield for the maturity, and \(h\) is the tenor of the forward contract expressed in fraction of years following each currency day count convention (BRL or USD).