Regression-based macro trading signals

This notebook illustrates the points discussed in the post “Regression-based macro trading signals” on the Macrosynergy website. It demonstrates how regression models can formulate trading signals based on macro indicators using the macrosynergy.learning subpackage, together with the popular scikit-learn package. The post applies a variety of statistical regression models to construct macro trading signals across three different asset class datasets (5-year interest rate swaps, equity index futures, and FX forward contracts). It summarizes both theoretical basics and empirical findings in order to provide guidance on using a variety of regression methods for macro trading strategy development.

The notebook is organized into four main sections:

• Get Packages and JPMaQS Data: This section is dedicated to installing and importing the necessary Python packages for the analysis. It includes standard Python libraries like pandas and seaborn, as well as the scikit-learn package and the specialized macrosynergy package.

• Transformations and Checks: In this part, the notebook conducts data calculations and transformations to derive relevant signals and targets for the analysis. This involves normalizing feature variables using z-scores and constructing simple linear composite indicators. The notebook tests three different strategies for the three major asset classes, and for each strategy, it considers a different set of plausible and speculative features. Every strategy calculates a conceptual risk parity signal, which is an unweighted average of plausible z-scored features for each strategy. These signals are assigned postfix _AVGZ

  • Duration strategy, with conceptual risk parity signal DU_AVGZ . Please see The power of macro trends in rates markets for the original version of this strategy

  • Equity strategy, with conceptual risk parity signal EQ_AVGZ . Please see Equity trend following and macro headwinds for the original version of this strategy

  • FX strategy, with conceptual risk parity signal FX_AVGZ . Please see Pure macro FX strategies: the benefits of double diversification for the original version of this strategy

• Predictions: The third part compares different regression-based signals with a natural benchmark, either a different regression-based signal or a conceptual risk parity signal, across rates, equity, and FX datasets. Signal comparison is done by three main criteria:

  • Correlation coefficients of the relation between month-end signals and next month’s target returns.

  • Accuracy and balanced accuracy of month-end signal-based predictions of the direction of next month’s returns.

  • Sharpe and Sortino ratios of naïve PnLs

• Regression comparisons: This part of the notebook compares first the average performance of the optimized OLS model from the previous section (averaged across rates, equity and FX strategies) with conceptual risk parity signal performance (also averaged across the three main strategies). Furthermore, additional optimized regression-based signals are compared to relevant benchmark models. Explored models are tested across each strategy (rates, equity, and FX), and key comparison parameters are averaged across these strategies and summarized in respective tables. The tested regression techniques include:

  • Non-negative least squares

  • Elastic net

  • Time-weighted least squares

  • Sign-weighted least squares

  • Least absolute deviations

  • KNN

A regression-based trading signal is a modified point-in-time regression forecast of returns. A regression model can employ several features (explanatory variables) and assign effective weights based on their past relations to target financial returns. The construction of point-in-time regression-based forecasts relies on a statistical learning process that generally involves three operations:

1. the sequential choice of an optimal regression model, based on past predictive performance,

2. a point-in-time estimation of its coefficients, and

3. the prediction of future returns based on that model.

This general method is attractive because regression is a well-understood way of relating explanatory/predictor variables (features) with dependent variables, here called target returns.

NOTE: This notebook is memory-intensive and time-intensive.

Get packages and JPMaQS data

This notebook primarily relies on the standard packages available in the Python data science stack. However, the macrosynergy package is additionally required for two purposes:

• Downloading JPMaQS data: The macrosynergy package facilitates the retrieval of JPMaQS data used in the notebook. For users using the free Kaggle subset , this part of the macrosynergy package is not required.

• For analyzing quantamental data and value propositions: The macrosynergy package provides functionality for performing quick analyses of quantamental data and exploring value propositions. The subpackage macrosynergy.learning integrates the macrosynergy package and associated JPMaQS data with the widely-used scikit-learn library and is used for sequential signal optimization.

For detailed information and a comprehensive understanding of the macrosynergy package and its functionalities, please refer to the “Introduction to Macrosynergy package” notebook on the Macrosynergy Quantamental Academy or visit the following link on Kaggle.

# Run only if needed!
"""
# %%capture
! pip install macrosynergy --upgrade"""

import os
import numpy as np
import pandas as pd

from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression, ElasticNet
from sklearn.neighbors import KNeighborsRegressor

from sklearn.metrics import (
    make_scorer,
    r2_score,
)

import macrosynergy.management as msm
import macrosynergy.panel as msp
import macrosynergy.pnl as msn
import macrosynergy.signal as mss
import macrosynergy.learning as msl
from macrosynergy.download import JPMaQSDownload

import warnings

warnings.simplefilter("ignore")

The JPMaQS indicators we consider are downloaded using the J.P. Morgan Dataquery API interface within the macrosynergy package. This is done by specifying ticker strings, formed by appending an indicator category code to a currency area code <cross_section>. These constitute the main part of a full quantamental indicator ticker, taking the form DB(JPMAQS,<cross_section>_<category>,<info>) , where denotes the time series of information for the given cross-section and category. The following types of information are available:

value giving the latest available values for the indicator eop_lag referring to days elapsed since the end of the observation period mop_lag referring to the number of days elapsed since the mean observation period grade denoting a grade of the observation, giving a metric of real time information quality.

After instantiating the JPMaQSDownload class within the macrosynergy.download module, one can use the download(tickers,start_date,metrics) method to easily download the necessary data, where tickers is an array of ticker strings, start_date is the first collection date to be considered and metrics is an array comprising the times series information to be downloaded. For more information see here or use the free dataset on Kaggle .

In the cell below, we specified cross-sections used for the analysis. For the abbreviations, please see About Dataset

# Cross-sections of interest - duration

cids_dm = ["AUD", "CAD", "CHF", "EUR", "GBP", "JPY", "NOK", "NZD", "SEK", "USD"]
cids_em = [
    "CLP",
    "COP",
    "CZK",
    "HUF",
    "IDR",
    "ILS",
    "INR",
    "KRW",
    "MXN",
    "PLN",
    "THB",
    "TRY",
    "TWD",
    "ZAR",
]
cids_du = cids_dm + cids_em
cids_dux = list(set(cids_du) - set(["IDR", "NZD"]))
cids_xg2 = list(set(cids_dux) - set(["EUR", "USD"]))

# Cross-sections of interest - equity

cids_g3 = ["EUR", "JPY", "USD"]  # DM large currency areas
cids_dmes = ["AUD", "CAD", "CHF", "GBP", "SEK"]  # Smaller DM equity countries
cids_eq = cids_g3 + cids_dmes  # DM equity countries

# Cross-sections of interest - FX
cids_dmsc = ["AUD", "CAD", "CHF", "GBP", "NOK", "NZD", "SEK"]  # DM small currency areas
cids_latm = ["BRL", "COP", "CLP", "MXN", "PEN"]  # Latam
cids_emea = ["CZK", "HUF", "ILS", "PLN", "RON", "RUB", "TRY", "ZAR"]  # EMEA
cids_emas = ["IDR", "INR", "KRW", "MYR", "PHP", "SGD", "THB", "TWD"]  # EM Asia ex China

cids_dm = cids_g3 + cids_dmsc
cids_em = cids_latm + cids_emea + cids_emas
cids = cids_dm + cids_em

cids_nofx = [
    "EUR",
    "USD",
    "JPY",
    "THB",
    "SGD",
    "RUB",
]  # not small or suitable for this analysis for lack of data
cids_fx = list(set(cids) - set(cids_nofx))

cids_dmfx = list(set(cids_dm).intersection(cids_fx))
cids_emfx = list(set(cids_em).intersection(cids_fx))

cids_eur = ["CHF", "CZK", "HUF", "NOK", "PLN", "RON", "SEK"]  # trading against EUR
cids_eud = ["GBP", "TRY"]  # trading against EUR and USD
cids_usd = list(set(cids_fx) - set(cids_eur + cids_eud))  # trading against USD

# Quantamental categories of interest

infs = [
    "CPIH_SA_P1M1ML12",
    "CPIC_SJA_P6M6ML6AR",
    "INFTEFF_NSA",
    "WAGES_NSA_P1M1ML12_3MMA",
    "PPIH_NSA_P1M1ML12",
]
grow = [
    "PCREDITBN_SJA_P1M1ML12",
    "RGDP_SA_P1Q1QL4_20QMA",
    "RGDP_SA_P1Q1QL4_20QMM",
    "INTRGDP_NSA_P1M1ML12_3MMA",
    "INTRGDPv5Y_NSA_P1M1ML12_3MMA",
    "RGDPTECH_SA_P1M1ML12_3MMA",
    "RGDPTECHv5Y_SA_P1M1ML12_3MMA",
    "IP_SA_P1M1ML12_3MMA",
]
surv = [
    "MBCSCORE_SA_D3M3ML3",
    "MBCSCORE_SA_D1Q1QL1",
    "MBCSCORE_SA_D6M6ML6",
    "MBCSCORE_SA_D2Q2QL2",
]
labs = [
    "EMPL_NSA_P1M1ML12_3MMA",
    "EMPL_NSA_P1Q1QL4",
    "WFORCE_NSA_P1Y1YL1_5YMM",
    "UNEMPLRATE_NSA_3MMA_D1M1ML12",
    "UNEMPLRATE_NSA_D1Q1QL4",
    "UNEMPLRATE_SA_D3M3ML3",
    "UNEMPLRATE_SA_D1Q1QL1",
    "UNEMPLRATE_SA_3MMA",
    "UNEMPLRATE_SA_3MMAv5YMM",
]

xbls = [
    "MTBGDPRATIO_SA_3MMA_D1M1ML3",
    "CABGDPRATIO_SA_3MMA_D1M1ML3",
    "CABGDPRATIO_SA_1QMA_D1Q1QL1",
    "MTBGDPRATIO_SA_6MMA_D1M1ML6",
    "CABGDPRATIO_SA_6MMA_D1M1ML6",
    "CABGDPRATIO_SA_2QMA_D1Q1QL2",
    "MTBGDPRATIO_SA_3MMAv60MMA",
    "CABGDPRATIO_SA_3MMAv60MMA",
    "CABGDPRATIO_SA_1QMAv20QMA",
]
tots = [
    "CTOT_NSA_P1M12ML1",
    "CTOT_NSA_P1M1ML12",
    "CTOT_NSA_P1M60ML1",
    "MTOT_NSA_P1M12ML1",
    "MTOT_NSA_P1M1ML12",
    "MTOT_NSA_P1M60ML1",
]

main = infs + grow + surv + labs + xbls + tots


mkts = [
    "FXTARGETED_NSA",
    "FXUNTRADABLE_NSA",
]

rets = [
    "DU05YXR_VT10",
    "EQXR_VT10",
    "EQXR_NSA",
    "FXXR_VT10",
]

xcats = main + mkts + rets

# Resultant tickers for download

single_tix = ["USD_GB10YXR_NSA"]
tickers = [cid + "_" + xcat for cid in cids for xcat in xcats] + single_tix

The description of each JPMaQS category is available either on the Macrosynergy Macro Quantamental Academy, or on JPMorgan Markets (password protected). In particular, the set used for this notebook is using Consumer price inflation trends , Inflation targets , Wage growth , PPI Inflation , Intuitive growth estimates , Domestic credit ratios , GDP growth , Technical GDP growth estimates , Industrial production trends , Private credit expansion , Manufacturing confidence scores , Demographic trends , Labor market dynamics , External ratios trends , Terms-of-trade , Duration returns , Equity index future returns , FX forward returns , and FX tradeability and flexibility

# Download series from J.P. Morgan DataQuery by tickers

start_date = "2000-01-01"
end_date = None

# Retrieve credentials

oauth_id = os.getenv("DQ_CLIENT_ID")  # Replace with own client ID
oauth_secret = os.getenv("DQ_CLIENT_SECRET")  # Replace with own secret

# Download from DataQuery

with JPMaQSDownload(client_id=oauth_id, client_secret=oauth_secret) as downloader:
    df = downloader.download(
        tickers=tickers,
        start_date=start_date,
        end_date=end_date,
        metrics=["value"],
        suppress_warning=True,
        show_progress=True,
    )

dfx = df.copy()
dfx.info()

Downloading data from JPMaQS.
Timestamp UTC:  2024-03-20 17:59:54
Connection successful!

Requesting data: 100%|█████████████████████████████████████████████████████████████████| 81/81 [00:18<00:00,  4.43it/s]
Downloading data: 100%|████████████████████████████████████████████████████████████████| 81/81 [00:22<00:00,  3.54it/s]

Some expressions are missing from the downloaded data. Check logger output for complete list.
306 out of 1613 expressions are missing. To download the catalogue of all available expressions and filter the unavailable expressions, set `get_catalogue=True` in the call to `JPMaQSDownload.download()`.
Some dates are missing from the downloaded data. 
2 out of 6320 dates are missing.
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 7868111 entries, 0 to 7868110
Data columns (total 4 columns):
 #   Column     Dtype         
---  ------     -----         
 0   real_date  datetime64[ns]
 1   cid        object        
 2   xcat       object        
 3   value      float64       
dtypes: datetime64[ns](1), float64(1), object(2)
memory usage: 240.1+ MB

Availability

It is essential to assess data availability before conducting any analysis. It allows for the identification of any potential gaps or limitations in the dataset, which can impact the validity and reliability of the analysis, ensure that a sufficient number of observations for each selected category and cross-section is available, and determine the appropriate periods for analysis.

For the purpose of the below presentation, we have renamed a collection of quarterly-frequency indicators to approximate monthly equivalents in order to have a full panel of similar measures across most countries. The two series’ are not identical but are close substitutes.

Rename quarterly indicators

dict_repl = {
    "EMPL_NSA_P1Q1QL4": "EMPL_NSA_P1M1ML12_3MMA",
    "WFORCE_NSA_P1Q1QL4_20QMM": "WFORCE_NSA_P1Y1YL1_5YMM",
    "UNEMPLRATE_NSA_D1Q1QL4": "UNEMPLRATE_NSA_3MMA_D1M1ML12",
    "WAGES_NSA_P1Q1QL4": "WAGES_NSA_P1M1ML12_3MMA",
    "UNEMPLRATE_SA_D1Q1QL1": "UNEMPLRATE_SA_D3M3ML3",
    "CABGDPRATIO_SA_1QMA_D1Q1QL1": "CABGDPRATIO_SA_3MMA_D1M1ML3",
    "CABGDPRATIO_SA_2QMA_D1Q1QL2": "CABGDPRATIO_SA_6MMA_D1M1ML6",
    "CABGDPRATIO_SA_1QMAv20QMA": "CABGDPRATIO_SA_3MMAv60MMA",
    "MBCSCORE_SA_D1Q1QL1": "MBCSCORE_SA_D3M3ML3",
    "MBCSCORE_SA_D2Q2QL2": "MBCSCORE_SA_D6M6ML6",
}

for key, value in dict_repl.items():
    dfx["xcat"] = dfx["xcat"].str.replace(key, value)

Check panel history

xcatx = infs
msm.check_availability(df=dfx, xcats=xcatx, cids=cids, missing_recent=False)

xcatx = grow
msm.check_availability(df=dfx, xcats=xcatx, cids=cids, missing_recent=False)

xcatx = surv
msm.check_availability(df=dfx, xcats=xcatx, cids=cids, missing_recent=False)

xcatx = xbls
msm.check_availability(df=dfx, xcats=xcatx, cids=cids, missing_recent=False)

xcatx = tots
msm.check_availability(df=dfx, xcats=xcatx, cids=cids, missing_recent=False)

FX-based blacklist dictionary

Identifying and isolating periods of official exchange rate targets, illiquidity, or convertibility-related distortions in FX markets is the first step in creating an FX trading strategy. These periods can significantly impact the behavior and dynamics of currency markets, and failing to account for them can lead to inaccurate or misleading findings. The make_blacklist() helper function creates a standardized dictionary of blacklist periods:

# Create blacklisting dictionary

dfb = df[df["xcat"].isin(["FXTARGETED_NSA", "FXUNTRADABLE_NSA"])].loc[
    :, ["cid", "xcat", "real_date", "value"]
]
dfba = (
    dfb.groupby(["cid", "real_date"])
    .aggregate(value=pd.NamedAgg(column="value", aggfunc="max"))
    .reset_index()
)
dfba["xcat"] = "FXBLACK"
fxblack = msp.make_blacklist(dfba, "FXBLACK")
fxblack

{'BRL': (Timestamp('2012-12-03 00:00:00'), Timestamp('2013-09-30 00:00:00')),
 'CHF': (Timestamp('2011-10-03 00:00:00'), Timestamp('2015-01-30 00:00:00')),
 'CZK': (Timestamp('2014-01-01 00:00:00'), Timestamp('2017-07-31 00:00:00')),
 'ILS': (Timestamp('2000-01-03 00:00:00'), Timestamp('2005-12-30 00:00:00')),
 'INR': (Timestamp('2000-01-03 00:00:00'), Timestamp('2004-12-31 00:00:00')),
 'MYR_1': (Timestamp('2000-01-03 00:00:00'), Timestamp('2007-11-30 00:00:00')),
 'MYR_2': (Timestamp('2018-07-02 00:00:00'), Timestamp('2024-03-19 00:00:00')),
 'PEN': (Timestamp('2021-07-01 00:00:00'), Timestamp('2021-07-30 00:00:00')),
 'RON': (Timestamp('2000-01-03 00:00:00'), Timestamp('2005-11-30 00:00:00')),
 'RUB_1': (Timestamp('2000-01-03 00:00:00'), Timestamp('2005-11-30 00:00:00')),
 'RUB_2': (Timestamp('2022-02-01 00:00:00'), Timestamp('2024-03-19 00:00:00')),
 'SGD': (Timestamp('2000-01-03 00:00:00'), Timestamp('2024-03-19 00:00:00')),
 'THB': (Timestamp('2007-01-01 00:00:00'), Timestamp('2008-11-28 00:00:00')),
 'TRY_1': (Timestamp('2000-01-03 00:00:00'), Timestamp('2003-09-30 00:00:00')),
 'TRY_2': (Timestamp('2020-01-01 00:00:00'), Timestamp('2024-03-19 00:00:00'))}

Transformation and checks

Duration feature candidates

To create a rates strategy, we develop a simple, plausible composite signal based on five features, including excess PPI inflation and excess industrial production growth as speculative signal candidates with presumed negative effects.

• Excess GDP growth trends

• Excess inflation

• Excess private credit growth

• Excess PPI inflation

• Excess industrial production growth

The original version of this strategy has been described in The power of macro trends in rates markets

Plausible features

# Excess GDP growth, excess inflation, excess private credit growth
calcs = [
    "XGDP_NEG = - INTRGDPv5Y_NSA_P1M1ML12_3MMA",
    "XCPI_NEG =  - ( CPIC_SJA_P6M6ML6AR + CPIH_SA_P1M1ML12 ) / 2 + INFTEFF_NSA",
    "XPCG_NEG = - PCREDITBN_SJA_P1M1ML12 + INFTEFF_NSA + RGDP_SA_P1Q1QL4_20QMA",
]

dfa = msp.panel_calculator(dfx, calcs=calcs, cids=cids_dux)
dfx = msm.update_df(dfx, dfa)

du_plaus = dfa["xcat"].unique().tolist()

Speculative features

Speculative features have weak theoretical backing, and their inclusion simulates the usage of inferior predictors in the signal-generating process.

calcs = [
    "XPPIH_NEG = - ( PPIH_NSA_P1M1ML12 - INFTEFF_NSA ) ",
    "XIPG_NEG =  - ( IP_SA_P1M1ML12_3MMA - RGDP_SA_P1Q1QL4_20QMA ) ",
]

dfa = msp.panel_calculator(dfx, calcs=calcs, cids=cids_dux)
dfx = msm.update_df(dfx, dfa)

du_specs = dfa["xcat"].unique().tolist()

Scores and composite

The process of standardizing the five indicators related to consumer spending and income prospects is achieved through the use of the make_zn_scores() function from the macrosynergy package. Normalization is a key step in macroeconomic analysis, especially when dealing with data across different categories that vary in units and time series characteristics. In this process, the indicators are centered around a neutral value (zero) using historical data. This normalization is recalculated monthly. To mitigate the impact of statistical outliers, a cutoff of 3 standard deviations is employed. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZNW3 , indicating their adjusted status.

The linear_composite method from the macrosynergy package is employed to aggregate the individual category scores into a unified composite indicator. This method offers the flexibility to assign specific weights to each category, which can vary over time. In this instance, equal weights are applied to all categories, resulting in a composite indicator referred to as DU_AVGZ . This approach ensures an even contribution from each category to the overall composite measure.

durs = du_plaus + du_specs
xcatx = durs

for xc in xcatx:
    dfa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cids_dux,
        neutral="zero",
        thresh=3,
        est_freq="M",
        pan_weight=1,
        postfix="_ZN3",
    )
    dfx = msm.update_df(dfx, dfa)

durz = [xc + "_ZN3" for xc in durs]

dfa = msp.linear_composite(
    df=dfx,
    xcats=durz,
    cids=cids_dux,
    new_xcat="DU_AVGZ",
)
dfx = msm.update_df(dfx, dfa)

The linear composite of the z-scores of all features used in rates strategy DU_AVGZ is displayed below with the help of view_timelines() from the macrosynergy package:

xcatx = ["DU_AVGZ"]

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Equity feature candidates

To create an equity strategy, we develop a simple, plausible composite signal based on five features, including excess PPI inflation and excess industrial production growth as speculative signal candidates with presumed negative effects.

• Labor market tightness

• Excess inflation

• Presumed index return momentum

• Excess PPI inflation

• Excess industrial production growth

This is loosely based on an original strategy described in Equity trend following and macro headwinds .

Plausible features

eq_plaus = []

Labor market tightness

Excess wage growth here is defined as wage growth per unit of output in excess of the effective estimated inflation target. Excess wage growth refers to the increase in wages relative to the growth in productivity or output, beyond what is considered consistent with the targeted level of inflation. It indicates a situation where wages are rising at a faster pace than can be justified by the prevailing inflation rate and the overall increase in economic output. Excess wage growth can contribute to inflationary pressures in the economy.

To proxy the impact of the business cycle state on employment growth, a common approach is to calculate the difference between employment growth and the long-term median of workforce growth. This difference is often referred to as “excess employment growth.” By calculating excess employment growth, one can estimate the component of employment growth that is attributable to the business cycle state. This measure helps to identify deviations from the long-term trend and provides insights into the cyclical nature of employment dynamics.

# Composite labor tightness score

calcs = [
    # Wage growth
    "LPGT = RGDP_SA_P1Q1QL4_20QMM - WFORCE_NSA_P1Y1YL1_5YMM ",  # labor productivity growth trend
    "XWAGES_NSA_P1M1ML12_3MMA = WAGES_NSA_P1M1ML12_3MMA - LPGT - INFTEFF_NSA ",  # excess wages
    "XWAGES_TREND_NEG = - XWAGES_NSA_P1M1ML12_3MMA ",
    # Employment growth
    "XEMPL_NSA_P1M1ML12_3MMA = EMPL_NSA_P1M1ML12_3MMA - WFORCE_NSA_P1Y1YL1_5YMM",
    "XEMPL_TREND_NEG = - XEMPL_NSA_P1M1ML12_3MMA",
    # Unemployment rate changes
    "XURATE_3Mv5Y = UNEMPLRATE_SA_3MMAv5YMM",
]

dfa = msp.panel_calculator(dfx, calcs=calcs, cids=cids_eq, blacklist=None)
dfx = msm.update_df(dfx, dfa)

As for the rates strategy, make_zn_scores() function from the macrosynergy package normalizes the indicators around a neutral value (zero) using historical data. This normalization is recalculated monthly. To mitigate the impact of statistical outliers, a cutoff of 2 standard deviations is employed. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZN , indicating their adjusted status.

# Score the equity features

xcatx = [
    "XEMPL_TREND_NEG",
    "XWAGES_TREND_NEG",
    "XURATE_3Mv5Y",
]
cidx = cids_eq

dfa = pd.DataFrame(columns=list(dfx.columns))

for xc in xcatx:
    dfaa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cidx,
        sequential=True,
        min_obs=261 * 5,
        neutral="zero",
        pan_weight=0.5,  # variance estimated based on panel and cross-sectional variation
        thresh=2,
        postfix="_ZN",
        est_freq="m",
    )
    dfa = msm.update_df(dfa, dfaa)

dfx = msm.update_df(dfx, dfa)
labz = [x + "_ZN" for x in xcatx]

linear_composite method from the macrosynergy package is employed to aggregate the individual category scores into a unified composite indicator LABSLACK_CZS with equal weights for each category for simplicity.

# Combine to a single score

xcatx = labz
czs = "LABSLACK_CZS"
cidx = cids_eq

dfa = msp.linear_composite(
    df=dfx,
    xcats=xcatx,
    cids=cidx,
    complete_xcats=False,
    new_xcat=czs,
)

dfx = msm.update_df(dfx, dfa)

if not czs in eq_plaus:
    eq_plaus.append(czs)

Inflation shortfall

Negative excess inflation is defined as the negative difference of chosen inflation trend and the effective inflation target INFTEFF_NSA

calcs = [
    "XCPIH_NEG = - CPIH_SA_P1M1ML12 + INFTEFF_NSA",
    "XCPIC_NEG =  - CPIC_SJA_P6M6ML6AR + INFTEFF_NSA",
]

dfa = msp.panel_calculator(dfx, calcs=calcs, cids=cids_eq)
dfx = msm.update_df(dfx, dfa)

xinfs = dfa["xcat"].unique().tolist()

As before, make_zn_scores() function from the macrosynergy package normalizes the indicators around a neutral value (zero) using historical data, recalculated monthly. with a cutoff of 2 standard deviations. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZN , indicating their adjusted status.

# Zn score the excess inflation features
cidx = cids_eq
sdate = "1990-01-01"

dfa = pd.DataFrame(columns=list(dfx.columns))

for xc in xinfs:
    dfaa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cidx,
        sequential=True,
        min_obs=261 * 5,
        neutral="zero",
        pan_weight=0.5,  # variance estimated based on panel and cross-sectional variation
        thresh=2,
        postfix="_ZN",
        est_freq="m",
    )
    dfa = msm.update_df(dfa, dfaa)

dfx = msm.update_df(dfx, dfa)
xinfz = [x + "_ZN" for x in xinfs]

The linear_composite method from the macrosynergy package aggregates the individual category scores into a unified composite indicator XCPI_NEG_CZS .

# Combine to a single score

xcatx = xinfz
czs = "XCPI_NEG_CZS"
cidx = cids_eq

dfa = msp.linear_composite(
    df=dfx,
    xcats=xcatx,
    cids=cidx,
    complete_xcats=False,
    new_xcat=czs,
)

dfx = msm.update_df(dfx, dfa)

if not czs in eq_plaus:
    eq_plaus.append(czs)

Return momentum

Here we take a standard equity trend indicator as the difference between 50-day and 200-day moving averages:

# Equity momentum

fxrs = ["EQXR_VT10", "EQXR_NSA"]
cidx = cids_eq

calcs = []
for fxr in fxrs:
    calc = [
        f"{fxr}I = ( {fxr} ).cumsum()",
        f"{fxr}I_50DMA = {fxr}I.rolling(50).mean()",
        f"{fxr}I_200DMA = {fxr}I.rolling(200).mean()",
        f"{fxr}I_50v200DMA = {fxr}I_50DMA - {fxr}I_200DMA",
    ]
    calcs += calc

dfa = msp.panel_calculator(dfx, calcs, cids=cidx)
dfx = msm.update_df(dfx, dfa)

eqtrends = ["EQXR_VT10I_50v200DMA", "EQXR_NSAI_50v200DMA"]

if not eqtrends[0] in eq_plaus:
    eq_plaus.append(eqtrends[0])

Speculative features

Speculative features here are the same as for the duration strategy. We use here negative excess inflation based on producer price inflation and negative excess industrial production growth. Both indicators have weak theoretical backing, and their inclusion simulates the usage of inferior predictors in the signal-generating process.

calcs = [
    "XPPIH_NEG = - ( PPIH_NSA_P1M1ML12 - INFTEFF_NSA ) ",
    "XIPG_NEG =  - ( IP_SA_P1M1ML12_3MMA - RGDP_SA_P1Q1QL4_20QMA ) ",
]

dfa = msp.panel_calculator(dfx, calcs=calcs, cids=cids_eq)
dfx = msm.update_df(dfx, dfa)

eq_specs = dfa["xcat"].unique().tolist()

Scores and composite

Once again, the make_zn_scores() function from the macrosynergy package normalizes the indicators around a neutral value (zero) using historical data. A cutoff of 3 standard deviations is employed. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZN3 , indicating their adjusted status. A combined, equally weighted indicator EQ_AVGZ is built using linear_composite method.

eqs = eq_plaus + eq_specs
xcatx = eqs

for xc in xcatx:
    dfa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cids_eq,
        neutral="zero",
        thresh=3,
        est_freq="M",
        pan_weight=1,
        postfix="_ZN3",
    )
    dfx = msm.update_df(dfx, dfa)

eqz = [xc + "_ZN3" for xc in eqs]

dfa = msp.linear_composite(
    df=dfx,
    xcats=eqz,
    cids=cids_eq,
    new_xcat="EQ_AVGZ",
)
dfx = msm.update_df(dfx, dfa)

The newly build composite unoptimized z-score for equity strategy EQ_AVGZ is displayed below with the help of view_timelines() from the macrosynergy package:

xcatx = ["EQ_AVGZ"]

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Foreign exchange feature candidates

To create a FX strategy, we develop a simple, plausible composite signal based on six features, including excess PPI inflation and excess industrial production growth as speculative signal candidates with presumed positive effects.

• Changes in external balance ratios

• Relative GDP growth trends

• Manufacturing survey score changes

• Terms-of-trade improvements

• Excess PPI inflation

• Excess industrial production growth

The original version of this strategy has been described in a Pure macro FX strategies: the benefits of double diversification .

Plausible features

fx_plaus = []

External ratio trends

In the cell below the External ratio trends are zn-scored around zero value, using zero as the neutral value, 3 as the cutoff value for winsorization in terms of standard deviations, 5 years of minimum number of observations, and monthly re-estimation frequency. Since the categories are homogeneous across countries, we use the whole panel as the basis for the parameters rather than individual cross-section.

# First Z-score each monthly external ratio change indicator
xcatx = [
    # Very short-term changes
    "MTBGDPRATIO_SA_3MMA_D1M1ML3",
    "CABGDPRATIO_SA_3MMA_D1M1ML3",
    # Short-term changes
    "MTBGDPRATIO_SA_6MMA_D1M1ML6",
    "CABGDPRATIO_SA_6MMA_D1M1ML6",
    # Medium-term changes
    "MTBGDPRATIO_SA_3MMAv60MMA",
    "CABGDPRATIO_SA_3MMAv60MMA",
]
cidx = cids_fx

dfa = pd.DataFrame(columns=list(dfx.columns))

for xc in xcatx:
    dfaa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cidx,
        sequential=True,
        min_obs=261 * 5,
        neutral="zero",
        pan_weight=1,
        thresh=3,
        postfix="_ZN",
        est_freq="m",
    )
    dfa = msm.update_df(dfa, dfaa)

dfx = msm.update_df(dfx, dfa)

xbdz = [xc + "_ZN" for xc in xcatx]

The linear_composite method from the macrosynergy package is employed to aggregate the individual category scores into a unified composite indicator XBT_ALL_CZS with equal weights for each category for simplicity.

# Combine to a single score

xcatx = xbdz
czs = "XBT_ALL_CZS"
cidx = cids_fx

dfa = msp.linear_composite(
    df=dfx,
    xcats=xcatx,
    cids=cidx,
    complete_xcats=False,
    new_xcat=czs,
)

dfx = msm.update_df(dfx, dfa)

if not czs in fx_plaus:
    fx_plaus.append(czs)

Relative growth trends

In the cell below we calculate the annual GDP growth trends relative to base currency area:

• Euro (‘CHF’, ‘CZK’, ‘HUF’, ‘NOK’, ‘PLN’, ‘RON’, ‘SEK’),

• USD (‘PEN’, ‘COP’, ‘IDR’, ‘THB’, ‘BRL’, ‘MXN’, ‘KRW’, ‘CAD’, ‘NZD’, ‘CLP’, ‘MYR’, ‘ZAR’, ‘AUD’, ‘TWD’, ‘INR’, ‘ILS’, ‘PHP’) or

• a simple average of the two for (‘GBP’, ‘TRY’).

The new indicators get postfix _vBM for “versus Benchmark”

The two cells below calculate the Annual GDP growth trend relative to base currency area and displays its timeline for each cross-section.

# Relative to base currency areas

xcatx = [
    # Intuitive growth estimates
    "INTRGDP_NSA_P1M1ML12_3MMA",
    "INTRGDPv5Y_NSA_P1M1ML12_3MMA",
    # Technical growth estimates
    "RGDPTECH_SA_P1M1ML12_3MMA",
    "RGDPTECHv5Y_SA_P1M1ML12_3MMA",
]

dfa = pd.DataFrame(columns=list(dfx.columns))
for xc in xcatx:
    calc_eur = [f"{xc}vBM = {xc} - iEUR_{xc}"]
    calc_usd = [f"{xc}vBM = {xc} - iUSD_{xc}"]
    calc_eud = [f"{xc}vBM = {xc} - 0.5 * ( iEUR_{xc} + iUSD_{xc} )"]

    dfa_eur = msp.panel_calculator(dfx, calcs=calc_eur, cids=cids_eur)
    dfa_usd = msp.panel_calculator(dfx, calcs=calc_usd, cids=cids_usd)
    dfa_eud = msp.panel_calculator(dfx, calcs=calc_eud, cids=cids_eud)

    dfa = msm.update_df(dfa, pd.concat([dfa_eur, dfa_usd, dfa_eud]))

dfx = msm.update_df(dfx, dfa)

grows = dfa["xcat"].unique().tolist()

The macrosynergy function make_zn_scores() normalizes the Annual GDP growth trend relative to the base currency area around zero adding _ZN postfix.

# Normalize relative growth

xcatx = grows
cidx = cids_fx

dfa = pd.DataFrame(columns=list(dfx.columns))

for xc in xcatx:
    dfaa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cidx,
        sequential=True,
        min_obs=261 * 5,
        neutral="zero",
        pan_weight=1,
        thresh=3,
        postfix="_ZN",
        est_freq="m",
    )
    dfa = msm.update_df(dfa, dfaa)

dfx = msm.update_df(dfx, dfa)
growz = [xc + "_ZN" for xc in xcatx]

The linear_composite method from the macrosynergy package is employed to aggregate the individual category scores into a unified composite indicator GDPvBM_CZS .

# Combine to a single score

xcatx = growz
czs = "GDPvBM_CZS"
cidx = cids_fx

dfa = msp.linear_composite(
    df=dfx,
    xcats=xcatx,
    cids=cidx,
    complete_xcats=False,
    new_xcat=czs,
)

dfx = msm.update_df(dfx, dfa)

if not czs in fx_plaus:
    fx_plaus.append(czs)

Manufacturing survey score changes

The make_zn_scores() function from the macrosynergy package normalizes the indicators around a neutral value (zero) using historical data. This normalization is recalculated monthly. To mitigate the impact of statistical outliers, a cutoff of 3 standard deviations is employed. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZN , indicating their adjusted status.

# Business score changes

xcatx = ["MBCSCORE_SA_D3M3ML3", "MBCSCORE_SA_D6M6ML6"]
cidx = cids_fx

dfa = pd.DataFrame(columns=list(dfx.columns))

for xc in xcatx:
    dfaa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cidx,
        sequential=True,
        min_obs=261 * 5,
        neutral="zero",
        pan_weight=1,
        thresh=3,
        postfix="_ZN",
        est_freq="m",
    )
    dfa = msm.update_df(dfa, dfaa)

dfx = msm.update_df(dfx, dfa)
survz = [xc + "_ZN" for xc in xcatx]

The linear_composite method from the macrosynergy package is employed to aggregate the individual category scores into a unified composite indicator MBSURVD_CZ with equal weights for each category for simplicity.

# Combine to a single score

xcatx = survz
czs = "MBSURVD_CZS"
cidx = cids_fx

dfa = msp.linear_composite(
    df=dfx,
    xcats=xcatx,
    cids=cidx,
    complete_xcats=False,
    new_xcat=czs,
)

dfx = msm.update_df(dfx, dfa)

if not czs in fx_plaus:
    fx_plaus.append(czs)

Terms-of-trade

The make_zn_scores() function from the macrosynergy package normalizes the indicators around a neutral value (zero) using historical data. This normalization is recalculated monthly. To mitigate the impact of statistical outliers, a cutoff of 3 standard deviations is employed. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZN , indicating their adjusted status.

xcatx = [
    # commodity-based changes
    "CTOT_NSA_P1M12ML1",
    "CTOT_NSA_P1M1ML12",
    "CTOT_NSA_P1M60ML1",
    # mixed dynamics
    "MTOT_NSA_P1M12ML1",
    "MTOT_NSA_P1M1ML12",
    "MTOT_NSA_P1M60ML1",
]

cidx = cids_fx
dfa = pd.DataFrame(columns=list(dfx.columns))

for xc in xcatx:
    dfaa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cidx,
        sequential=True,
        min_obs=261 * 5,
        neutral="zero",
        pan_weight=0.5,  # 50% cross-section weight as ToT changes are not fully comparable
        thresh=3,
        postfix="_ZN",
        est_freq="m",
    )
    dfa = msm.update_df(dfa, dfaa)

dfx = msm.update_df(dfx, dfa)
ttdz = [xc + "_ZN" for xc in xcatx]

The linear_composite method from the macrosynergy package is employed to aggregate the individual category scores into a unified composite indicator TTD_ALL_CZS with equal weights for each category for simplicity.

# Combine to a single score

xcatx = ttdz
czs = "TTD_ALL_CZS"
cidx = cids_fx

dfa = msp.linear_composite(
    df=dfx,
    xcats=xcatx,
    cids=cidx,
    complete_xcats=False,
    new_xcat=czs,
)

dfx = msm.update_df(dfx, dfa)

if not czs in fx_plaus:
    fx_plaus.append(czs)

Speculative features

Speculative features here are the same as for the previous strategies: the negative excess inflation based on producer price inflation and negative excess industrial production growth. Both indicators have weak theoretical backing, and their inclusion simulates the usage of inferior predictors in the signal-generating process.

calcs = [
    "XPPIH = PPIH_NSA_P1M1ML12 - INFTEFF_NSA ",
    "XIPG =  IP_SA_P1M1ML12_3MMA - RGDP_SA_P1Q1QL4_20QMA ",
]

dfa = msp.panel_calculator(dfx, calcs=calcs, cids=cids_fx)
dfx = msm.update_df(dfx, dfa)

fx_specs = dfa["xcat"].unique().tolist()

Scores and composite

Once again, the make_zn_scores() function from the macrosynergy package normalizes the indicators around a neutral value (zero) using historical data. A cutoff of 3 standard deviations is employed. Post-normalization, the indicators (z-scores) are labeled with the suffix _ZN3 , indicating their adjusted status. A combined, equally weighted indicator is built using linear_composite method. The new (unoptimized) signal receives the name FX_AVGZ

fxs = fx_plaus + fx_specs
xcatx = fxs

for xc in xcatx:
    dfa = msp.make_zn_scores(
        dfx,
        xcat=xc,
        cids=cids_fx,
        neutral="zero",
        thresh=3,
        est_freq="M",
        pan_weight=1,
        postfix="_ZN3",
    )
    dfx = msm.update_df(dfx, dfa)

fxz = [xc + "_ZN3" for xc in fxs]

dfa = msp.linear_composite(
    df=dfx,
    xcats=fxz,
    cids=cids_fx,
    new_xcat="FX_AVGZ",
)
dfx = msm.update_df(dfx, dfa)

The linear composite of the z-scores of all features used in fx strategy FX_AVGZ is displayed below with the help of view_timelines() from the macrosynergy package:

xcatx = ["FX_AVGZ"]

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Features and targets for scikit-learn

As the first preparation for the statistical learning modelling, we downsample the daily information states to monthly frequency with the help of the categories_df() function applying the lag of 1 month and using the last value in the month for explanatory variables and sum for the aggregated target (return). Two dataframes for each strategy are defined:

• feature dataframe X_du and target dataframe y_du for the duration strategy

• feature dataframe X_eq and target dataframe y_eq for the equity strategy

• feature dataframe X_fx and target dataframe y_fx for the fx strategy

Duration

# Specify features and target category
xcatx = durz + ["DU05YXR_VT10"]

# Downsample from daily to monthly frequency (features as last and target as sum)
dfw = msm.categories_df(
    df=dfx,
    xcats=xcatx,
    cids=cids_dux,
    freq="M",
    lag=1,
    blacklist=fxblack,
    xcat_aggs=["last", "sum"],
)

# Drop rows with missing values and assign features and target
dfw.dropna(inplace=True)
X_du = dfw.iloc[:, :-1]
y_du = dfw.iloc[:, -1]

Equity

# Specify features and target category
xcatx = eqz + ["EQXR_VT10"]

# Downsample from daily to monthly frequency (features as last and target as sum)
dfw = msm.categories_df(
    df=dfx,
    xcats=xcatx,
    cids=cids_eq,
    freq="M",
    lag=1,
    blacklist=None,
    xcat_aggs=["last", "sum"],
)

# Drop rows with missing values and assign features and target
dfw.dropna(inplace=True)
X_eq = dfw.iloc[:, :-1]
y_eq = dfw.iloc[:, -1]

FX

# Specify features and target category
xcatx = fxz + ["FXXR_VT10"]

# Downsample from daily to monthly frequency (features as last and target as sum)
dfw = msm.categories_df(
    df=dfx,
    xcats=xcatx,
    cids=cids_fx,
    freq="M",
    lag=1,
    blacklist=fxblack,
    xcat_aggs=["last", "sum"],
)

# Drop rows with missing values and assign features and target
dfw.dropna(inplace=True)
X_fx = dfw.iloc[:, :-1]
y_fx = dfw.iloc[:, -1]

Prediction

Here we use standard R2 score for evaluating the performance of regression models.

# Define the optimization criterion
scorer = make_scorer(r2_score, greater_is_better=True)

# Define splits for cross-validation
splitter = msl.RollingKFoldPanelSplit(n_splits=5)

Ordinary least squares

We test the consequences of using a standard learning process with standard ordinary least squares (OLS) regression to condense the information of multiple candidate features, against a standard conceptual risk parity benchmark. The only important hyperparameter to optimize over is the inclusion of an intercept in the regression. Although all features have a theoretical neutral level at zero, an intercept would correct for any errors in the underlying assumptions. Yet, the price for potential bias is that past long-term seasons of positive or negative target returns translate into sizable intercepts and future directional bias of the regression signal.

Duration

mods_du_ols = {
    "ols": LinearRegression(),
}

grid_du_ols = {
    "ols": {"fit_intercept": [True, False]},
}

The following cell uses the macrosynergy.learning.SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled DU_OLS

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)

so_du.calculate_predictions(
    name="DU_OLS",
    models=mods_du_ols,
    hparam_grid=grid_du_ols,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_OLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 241/241 [00:05<00:00, 40.72it/s]

None

Both signals DU_AVGZ , DU_OLS are displayed below with the help of view_timelines() from the macrosynergy package:

sigs_du_ols = ["DU_AVGZ", "DU_OLS"]
xcatx = sigs_du_ols

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

This section uses extensively the following classes of the macrosynergy package:

• SignalReturnRelations

• NaivePnL

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_du_ols = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs_du_ols,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    blacklist=fxblack,
    slip=1,
)

srr_du_ols.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_AVGZ	0.516	0.517	0.484	0.534	0.552	0.482	0.071	0.0	0.040	0.0	0.517
DU_OLS	0.537	0.526	0.817	0.534	0.544	0.508	0.052	0.0	0.037	0.0	0.516

We estimate the economic value of both composite signals based on a naïve PnL computed according to a standard procedure used in Macrosynergy research posts. A naive PnL is calculated for simple monthly rebalancing in accordance with the composite scores DU_AVGZ and DU_OLS and score at the end of each month as the basis for the positions of the next month and under consideration of a 1-day slippage for trading. The trading signals are capped at 2 standard deviations in either direction for each currency as a reasonable risk limit, and applied to volatility-targeted positions. This means that one unit of signal translates into one unit of risk (approximated by estimated return volatility) for each currency. The naïve PnL does not consider transaction costs or compounding. For the chart below, the PnL has been scaled to an annualized volatility of 10%

sigs = sigs_du_ols
cidx = cids_dux

pnl_du_ols = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs,
    cids=cidx,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_ols.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_du_ols.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)
pnl_du_ols.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_AVGZ	PNL_DU_OLS
Return (pct ar)	4.693902	4.775803
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.46939	0.47758
Sortino Ratio	0.666395	0.664932
Max 21-day draw	-29.084247	-23.232096
Max 6-month draw	-40.889334	-50.30782
USD_GB10YXR_NSA correl	-0.057391	0.396561
Traded Months	243	243

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_du_ols = msn.create_results_dataframe(
    title="Performance metrics, PARITY vs OLS, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_ols,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    sig_negs=[False, False],
    neutrals="zero",
    threshs=2,
    bm="USD_GB10YXR_NSA",
    cosp=True,
    start="2004-01-01",
    blacklist=fxblack,
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_AVGZ": "PARITY", "DU_OLS": "OLS"},
    slip=1,
)
results_du_ols

Performance metrics, PARITY vs OLS, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
PARITY	0.516	0.517	0.071	0.040	0.469	0.666	-0.057
OLS	0.537	0.526	0.052	0.037	0.478	0.665	0.397

Equity

mods_eq_ols = {
    "ols": LinearRegression(),
}

grid_eq_ols = {
    "ols": {"fit_intercept": [True, False]},
}

As for the duration strategy above, we deploy macrosynergy's SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. In this context, we aim to generate the signal for the equity strategy EQ_OLS , which will then be analyzed in comparison to the previously developed conceptual parity signal, EQ_AVGZ .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)

so_eq.calculate_predictions(
    name="EQ_OLS",
    models=mods_eq_ols,
    hparam_grid=grid_eq_ols,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_OLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 245/245 [00:00<00:00, 280.43it/s]

None

Both signals EQ_AVGZ , EQ_OLS are displayed below with the help of view_timelines() from the macrosynergy package:

sigs_eq_ols = ["EQ_AVGZ", "EQ_OLS"]
xcatx = sigs_eq_ols

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class from the macrosynergy.signal module is designed to analyze, visualize, and compare the relationships between panels of trading signals and panels of subsequent returns and signals_table() method is used for a comparative overview of the signal-return relationship across both signals.

## Compare optimized signals with simple average z-scores

srr_eq_ols = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs_eq_ols,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_ols.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_AVGZ	0.577	0.558	0.588	0.619	0.667	0.449	0.119	0.000	0.073	0.000	0.559
EQ_OLS	0.564	0.521	0.696	0.619	0.632	0.410	0.053	0.021	0.035	0.022	0.519

We estimate the economic value of both composite signals based on a naïve PnL computed according to a standard procedure used in Macrosynergy research posts. A naive PnL is calculated for simple monthly rebalancing in accordance with the composite scores EQ_AVGZ and EQ_OLS and score at the end of each month as the basis for the positions of the next month and under consideration of a 1-day slippage for trading. The trading signals are capped at 2 standard deviations in either direction for each currency as a reasonable risk limit, and applied to volatility-targeted positions. This means that one unit of signal translates into one unit of risk (approximated by estimated return volatility) for each currency. The naïve PnL does not consider transaction costs or compounding. For the chart below, the PnL has been scaled to an annualized volatility of 10%

cidx = cids_eq
sigs = sigs_eq_ols

pnl_eq_ols = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cidx,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_eq_ols.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_eq_ols.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_eq_ols.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_EQ_AVGZ	PNL_EQ_OLS
Return (pct ar)	6.83752	5.8943
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.683752	0.58943
Sortino Ratio	0.98746	0.810566
Max 21-day draw	-23.755176	-27.401221
Max 6-month draw	-17.406019	-19.593067
USD_EQXR_NSA correl	0.037089	0.206792
Traded Months	243	243

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_eq_ols = msn.create_results_dataframe(
    title="Performance metrics, PARITY vs OLS, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_ols,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    sig_negs=[False, False],
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_AVGZ": "PARITY", "EQ_OLS": "OLS"},
    slip=1,
)
results_eq_ols

Performance metrics, PARITY vs OLS, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
PARITY	0.577	0.558	0.119	0.073	0.684	0.987	0.037
OLS	0.564	0.521	0.053	0.035	0.589	0.811	0.207

FX

mods_fx_ols = {
    "ols": LinearRegression(),
}

grid_fx_ols = {
    "ols": {"fit_intercept": [True, False]},
}

The same steps are repeated for the FX strategy. The following cell uses the macrosynergy.learning.SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The OLS signal derived in the process receives label FX_OLS .

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)

so_fx.calculate_predictions(
    name="FX_OLS",
    models=mods_fx_ols,
    hparam_grid=grid_fx_ols,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_OLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 242/242 [00:00<00:00, 257.29it/s]

None

Both signals FX_AVGZ , FX_OLS are displayed below with the help of view_timelines() from the macrosynergy package:

sigs_fx_ols = ["FX_AVGZ", "FX_OLS"]
xcatx = sigs_fx_ols

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class from the macrosynergy.signal module is designed to analyze, visualize, and compare the relationships between panels of trading signals and panels of subsequent returns.

## Compare optimized signals with simple average z-scores

srr_fx_ols = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs_fx_ols,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    blacklist=fxblack,
    slip=1,
)

srr_fx_ols.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_AVGZ	0.515	0.513	0.520	0.537	0.550	0.477	0.037	0.006	0.028	0.002	0.513
FX_OLS	0.527	0.516	0.677	0.537	0.547	0.484	0.023	0.090	0.024	0.009	0.514

NaivePnl() class is designed to provide a quick and simple overview of a stylized PnL profile of a set of trading signals. The class is labeled naive because its methods do not consider transaction costs or position limitations, such as risk management considerations. This is deliberate because costs and limitations are specific to trading size, institutional rules, and regulations.

sigs = sigs_fx_ols

pnl_fx_ols = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_fx_ols.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_fx_ols.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)
pnl_fx_ols.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_FX_AVGZ	PNL_FX_OLS
Return (pct ar)	5.845293	2.890297
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.584529	0.28903
Sortino Ratio	0.828437	0.397751
Max 21-day draw	-19.16154	-23.927897
Max 6-month draw	-34.009985	-21.753265
USD_EQXR_NSA correl	-0.059992	0.105992
Traded Months	243	243

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_fx_ols = msn.create_results_dataframe(
    title="Performance metrics, PARITY vs OLS, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_ols,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    sig_negs=[False, False],
    
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    blacklist=fxblack,
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_AVGZ": "PARITY", "FX_OLS": "OLS"},
    slip=1,
)
results_fx_ols

Performance metrics, PARITY vs OLS, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
PARITY	0.515	0.513	0.037	0.028	0.585	0.828	-0.060
OLS	0.527	0.516	0.023	0.024	0.289	0.398	0.106

Regression comparison

OLS failed to outperform conceptual parity on average for the three types of macro strategies. Whilst the accuracy of OLS signals was higher balanced accuracy, forward correlation coefficients and PnL performance ratios were all lower. Also, market benchmark correlation of OLS-based strategies was on average higher. Underperformance of OLS mainly arose in the FX space and reflected the learning method’s preference for regression models with intercept from 2008 to 2014, which translated the strong season for FX returns of the earlier 2000s into a positive bias for signals during and after the great financial crisis.

The empirical analysis provided two important lessons:

• Only allow constants if there is a good reason. If the regression intercept picks up longer performance seasons, it will simply extrapolate past return averages.

• Don’t compare regression signals and fixed-weight signals by correlation metrics. Regression-based signal variation does not arise merely from feature variation, but from changes in model parameters and hyperparameters. And the latter sources of variation have no plausible relation to target return. For example, in the empirical analyses of the duration strategy the OLS signals post lower predictive correlation but produce higher accuracy and balanced accuracy and almost the same performance ratios.

results_ols = (results_du_ols.data + results_eq_ols.data + results_fx_ols.data) / 3
results_ols.style.format("{:.3f}").set_caption(
    "Averaged performance metrics, PARITY vs OLS"
).set_table_styles(
    [
        {
            "selector": "caption",
            "props": [("text-align", "center"), ("font-weight", "bold")],
        }
    ]
)

Averaged performance metrics, PARITY vs OLS

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
PARITY	0.536	0.529	0.076	0.047	0.579	0.827	-0.027
OLS	0.543	0.521	0.043	0.032	0.452	0.625	0.237

Non-negative least squares

NNLS is a regression technique used to approximate the solution of an overdetermined system of linear equations with the additional constraint that the coefficients must be non-negative. This is a bit like placing independent half-flat priors on the feature weights in a Bayesian context. The main advantage of NNLS is that it allows consideration of theoretical priors, reducing dependence on scarce data.

Duration

mods_du_ls = {
    "nnls": LinearRegression(positive=True),
}

grid_du_ls = {
    "nnls": {"fit_intercept": [True, False]},
}

The following cell uses the macrosynergy.learning.SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The signal generated through this process is labeled as DU_NNLS .

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)

so_du.calculate_predictions(
    name="DU_NNLS",
    models=mods_du_ls,
    hparam_grid=grid_du_ls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_NNLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 241/241 [00:00<00:00, 267.55it/s]

None

Both signals DU_NNLS , and DU_OLS are displayed below with the help of view_timelines() from the macrosynergy package:

sigs_du_ls = ["DU_OLS", "DU_NNLS"]
xcatx = sigs_du_ls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

# Compare optimized signals with simple average z-scores

xcatx = sigs_du_ls

srr_du_ls = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=xcatx,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    blacklist=fxblack,
    slip=1,
)

srr_du_ls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_OLS	0.537	0.526	0.817	0.534	0.544	0.508	0.052	0.0	0.037	0.0	0.516
DU_NNLS	0.536	0.524	0.860	0.534	0.541	0.506	0.066	0.0	0.047	0.0	0.511

sigs = sigs_du_ls

pnl_du_ls = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs,
    cids=cids_dux,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_ls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_du_ls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)
pnl_du_ls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_NNLS	PNL_DU_OLS
Return (pct ar)	5.596688	4.864396
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.559669	0.48644
Sortino Ratio	0.780315	0.674827
Max 21-day draw	-23.576246	-23.241644
Max 6-month draw	-32.555519	-50.273484
USD_GB10YXR_NSA correl	0.458233	0.396898
Traded Months	242	242

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_du_ls = msn.create_results_dataframe(
    title="Performance metrics, OLS vs NNLS, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_ls,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    sig_negs=[False, False],
    threshs=2,
    bm="USD_GB10YXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_OLS": "OLS", "DU_NNLS": "NNLS"},
    slip=1,
    blacklist=fxblack,
)
results_du_ls

Performance metrics, OLS vs NNLS, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
NNLS	0.536	0.524	0.066	0.047	0.551	0.768	0.458
OLS	0.537	0.526	0.052	0.037	0.478	0.662	0.397

Equity

mods_eq_ls = {
    "nnls": LinearRegression(positive=True),
}

grid_eq_ls = {
    "nnls": {"fit_intercept": [True, False]},
}

The following cell uses the macrosynergy.learning.SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The signal generated through this process is labeled as EQ_NNLS .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)

so_eq.calculate_predictions(
    name="EQ_NNLS",
    models=mods_eq_ls,
    hparam_grid=grid_eq_ls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_NNLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 245/245 [00:00<00:00, 357.13it/s]

None

Both signals EQ_NNLS , and EQ_OLS are displayed below with the help of view_timelines() from the macrosynergy package:

sigs_eq_ls = ["EQ_OLS", "EQ_NNLS"]
xcatx = sigs_eq_ls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_eq_ls = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs_eq_ls,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_ls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_OLS	0.564	0.521	0.696	0.619	0.632	0.410	0.053	0.021	0.035	0.022	0.519
EQ_NNLS	0.571	0.530	0.693	0.619	0.637	0.422	0.072	0.002	0.045	0.003	0.527

sigs = sigs_eq_ls

pnl_eq_ls = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cids_eq,
    bms=["USD_EQXR_NSA"],
    start="2004-01-01",
)
for sig in sigs:
    pnl_eq_ls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_eq_ls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)
pnl_eq_ls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_EQ_NNLS	PNL_EQ_OLS
Return (pct ar)	6.420837	5.8943
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.642084	0.58943
Sortino Ratio	0.885607	0.810566
Max 21-day draw	-27.347989	-27.401221
Max 6-month draw	-19.328926	-19.593067
USD_EQXR_NSA correl	0.160998	0.206792
Traded Months	243	243

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_eq_ls = msn.create_results_dataframe(
    title="Performance metrics, NNLS vs OLS, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_ls,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    sig_negs=[False, False],
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_OLS": "OLS", "EQ_NNLS": "NNLS"},
    slip=1,
)
results_eq_ls

Performance metrics, NNLS vs OLS, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
NNLS	0.571	0.530	0.072	0.045	0.642	0.886	0.161
OLS	0.564	0.521	0.053	0.035	0.589	0.811	0.207

FX

mods_fx_ls = {
    "nnls": LinearRegression(positive=True),
}

grid_fx_ls = {
    "nnls": {"fit_intercept": [True, False]},
}

As before, we deploy SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The signal generated through this process is labeled as FX_NNLS

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)

so_fx.calculate_predictions(
    name="FX_NNLS",
    models=mods_fx_ls,
    hparam_grid=grid_fx_ls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_NNLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 242/242 [00:00<00:00, 247.03it/s]

None

Both signals FX_NNLS , and FX_OLS are displayed below with the help of view_timelines() from the macrosynergy package:

sigs_fx_ls = ["FX_OLS", "FX_NNLS"]
xcatx = sigs_fx_ls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_fx_ls = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs_fx_ls,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_fx_ls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_OLS	0.527	0.516	0.677	0.537	0.547	0.484	0.023	0.090	0.024	0.009	0.514
FX_NNLS	0.529	0.519	0.664	0.537	0.550	0.488	0.028	0.038	0.027	0.003	0.517

sigs = sigs_fx_ls

pnl_fx_ls = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    blacklist=fxblack,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_fx_ls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_fx_ls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)
pnl_fx_ls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_FX_NNLS	PNL_FX_OLS
Return (pct ar)	3.630384	2.890297
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.363038	0.28903
Sortino Ratio	0.500385	0.396959
Max 21-day draw	-25.206937	-23.927897
Max 6-month draw	-23.098425	-21.753265
USD_EQXR_NSA correl	0.093248	0.105992
Traded Months	243	243

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_fx_ls = msn.create_results_dataframe(
    title="Performance metrics, NNLS vs OLS, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_ls,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    sig_negs=[False, False],
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_OLS": "OLS", "FX_NNLS": "NNLS"},
    slip=1,
    blacklist=fxblack,
)
results_fx_ls

Performance metrics, NNLS vs OLS, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
NNLS	0.529	0.519	0.028	0.027	0.363	0.500	0.093
OLS	0.527	0.516	0.023	0.024	0.289	0.397	0.106

Comparison

NNLS-based learning outperforms OLS-based learning based on all averages of performance metrics. PnL outperformance is small and gentle overtime, but consistent across time and types of strategies.

The empirical analysis provided two important lessons:

• NNLS produces greater model stability. This is mainly because NNLS excludes all theoretically implausible contributors to the signals and thus reduces the model construction options of the learning process.

• The benefits of NNLS may only show only very gradually. In our data example, NNLS is not a game changer compared to OLS. Signals are broadly similar, which is not surprising, given that we only used a small set of features, most of which are conceptually different. However, long-term correlations and performance ratios ended up higher for all strategies over the 20 year periods.

results_ls = (results_du_ls.data + results_eq_ls.data + results_fx_ls.data) / 3
results_ls.style.format("{:.3f}").set_caption(
    "Averaged performance metrics, NNLS vs OLS"
).set_table_styles(
    [
        {
            "selector": "caption",
            "props": [("text-align", "center"), ("font-weight", "bold")],
        }
    ]
)

Averaged performance metrics, NNLS vs OLS

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
NNLS	0.545	0.524	0.055	0.040	0.519	0.718	0.237
OLS	0.543	0.521	0.043	0.032	0.452	0.623	0.237

Elastic net

Elastic net is a flexible form of regularized regression. Regularization adds penalties to a model’s objective function, often in accordance with the size of coefficients, in order to prevent overfitting. In the case of regression, the Lasso and Ridge models are employed to that end. Lasso penalizes the absolute size of coefficients (L1 penalty), which is shrinking coefficients, possibly all the way to zero. Ridge penalizes the squared size of coefficients (L2 penalty), which just shrinks the absolute value of coefficients. Elastic Net combines both L1 and L2 penalties.

Duration

mods_du_en = {
    "en": Pipeline(
        [
            ("scaler", msl.PanelStandardScaler()),
            ("en", ElasticNet()),
        ]
    ),
}

grid_du_en = {
    "en": {
        "en__l1_ratio": [0.1, 0.25, 0.5, 0.75, 0.9],
        "en__alpha": [
            1e-4,
            1e-3,
            1e-2,
            1e-1,
            1,
            10,
            100,
            1000,
        ],
        "en__positive": [True, False],
        "en__fit_intercept": [True, False],
    },
}

mods_du_ls = {
    "ls": LinearRegression(),
}

grid_du_ls = {
    "ls": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
}

As previously, the SignalOptimizer class is used for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled DU_EN .

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)

# Elastic net
so_du.calculate_predictions(
    name="DU_EN",
    models=mods_du_en,
    hparam_grid=grid_du_en,
    metric=scorer,
    min_cids=4,
    min_periods=36,
    n_jobs=-1,
)

som = so_du.models_heatmap(name="DU_EN", figsize=(18, 6))
display(som)

# OLS/ NNLS
so_du.calculate_predictions(
    name="DU_LS",
    models=mods_du_ls,
    hparam_grid=grid_du_ls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_LS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 241/241 [02:17<00:00,  1.76it/s]

None

100%|███████████████████████████████████████████████████████████████████████████████| 241/241 [00:02<00:00, 108.60it/s]

None

The view_timelines() function in the macrosynergy package is used to display the signals: DU_EN and DU_LS .

sigs_du_en = ["DU_EN", "DU_LS"]
xcatx = sigs_du_en

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_du_en = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs_du_en,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_du_en.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_EN	0.526	0.510	0.878	0.529	0.532	0.488	0.043	0.003	0.030	0.002	0.504
DU_LS	0.532	0.516	0.849	0.534	0.539	0.493	0.048	0.001	0.029	0.003	0.508

## Compare optimized signals with simple average z-scores

srr_du_en = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs_du_en,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_du_en.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_EN	0.526	0.510	0.878	0.529	0.532	0.488	0.043	0.003	0.030	0.002	0.504
DU_LS	0.532	0.516	0.849	0.534	0.539	0.493	0.048	0.001	0.029	0.003	0.508

sigs = sigs_du_en

pnl_du_en = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs,
    cids=cids_dux,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_en.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_du_en.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_du_en.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_EN	PNL_DU_LS
Return (pct ar)	4.041855	4.294597
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.404185	0.42946
Sortino Ratio	0.561508	0.594083
Max 21-day draw	-26.470975	-24.904755
Max 6-month draw	-36.526518	-34.397224
USD_GB10YXR_NSA correl	0.465463	0.450925
Traded Months	242	242

The method create_results_dataframe() from macrosynergy.pnl displays a small dataframe of key statistics for both signals:

results_du_en = msn.create_results_dataframe(
    title="Performance metrics, Elastic Net vs Least Squares, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_en,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    sig_negs=[False, False],
    threshs=2,
    bm="USD_GB10YXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_LS": "LS", "DU_EN": "EN"},
    slip=1,
    blacklist=fxblack,
)
results_du_en

Performance metrics, Elastic Net vs Least Squares, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
EN	0.526	0.510	0.043	0.030	0.404	0.562	0.465
LS	0.532	0.516	0.048	0.029	0.429	0.594	0.451

Equity

mods_eq_en = {
    "en": Pipeline(
        [
            ("scaler", msl.PanelStandardScaler()),
            ("en", ElasticNet()),
        ]
    ),
}

grid_eq_en = {
    "en": {
        "en__l1_ratio": [0.1, 0.25, 0.5, 0.75, 0.9],
        "en__alpha": [
            1e-4,
            1e-3,
            1e-2,
            1e-1,
            1,
            10,
            100,
            1000,
        ],
        "en__positive": [True, False],
        "en__fit_intercept": [True, False],
    },
}

mods_eq_ls = {
    "ls": LinearRegression(),
}

grid_eq_ls = {
    "ls": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
}

As previously, the SignalOptimizer class is used for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled EQ_EN .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)

# EN
so_eq.calculate_predictions(
    name="EQ_EN",
    models=mods_eq_en,
    hparam_grid=grid_eq_en,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_EN", figsize=(18, 6))
display(som)

# OLS
so_eq.calculate_predictions(
    name="EQ_LS",
    models=mods_eq_ls,
    hparam_grid=grid_eq_ls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_LS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 245/245 [02:13<00:00,  1.83it/s]

None

100%|███████████████████████████████████████████████████████████████████████████████| 245/245 [00:01<00:00, 129.85it/s]

None

The view_timelines() function in the macrosynergy package displays both signals EQ_EN and EQ_LS .

sigs_eq_en = ["EQ_LS", "EQ_EN"]
xcatx = sigs_eq_en

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_eq_en = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs_eq_en,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_en.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_LS	0.564	0.521	0.693	0.619	0.632	0.411	0.065	0.005	0.038	0.013	0.519
EQ_EN	0.574	0.535	0.705	0.610	0.631	0.439	0.071	0.002	0.042	0.006	0.531

sigs = sigs_eq_en

pnl_eq_en = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cids_eq,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_eq_en.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_eq_en.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_eq_en.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_EQ_EN	PNL_EQ_LS
Return (pct ar)	6.394354	6.125482
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.639435	0.612548
Sortino Ratio	0.877459	0.845046
Max 21-day draw	-33.162327	-27.600217
Max 6-month draw	-21.490043	-19.515294
USD_EQXR_NSA correl	0.181874	0.170386
Traded Months	243	243

results_eq_en = msn.create_results_dataframe(
    title="Performance metrics, Elastic Net vs Least Squares, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_en,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    sig_negs=[False, False],
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_LS": "LS", "EQ_EN": "EN"},
    slip=1,
)
results_eq_en

Performance metrics, Elastic Net vs Least Squares, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
EN	0.574	0.535	0.071	0.042	0.639	0.877	0.182
LS	0.564	0.521	0.065	0.038	0.613	0.845	0.170

FX

mods_fx_en = {
    "en": Pipeline(
        [
            ("scaler", msl.PanelStandardScaler()),
            ("en", ElasticNet(max_iter=10000)),
        ]
    ),
}

grid_fx_en = {
    "en": {
        "en__l1_ratio": [0.1, 0.25, 0.5, 0.75, 0.9],
        "en__alpha": [
            1e-4,
            1e-3,
            1e-2,
            1e-1,
            1,
            10,
            100,
            1000,
        ],
        "en__positive": [True, False],
        "en__fit_intercept": [True, False],
    },
}

mods_fx_ls = {
    "ls": LinearRegression(),
}

grid_fx_ls = {
    "ls": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
}

As previously, the SignalOptimizer class for sequential optimization of raw signals is based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled FX_EN .

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)

# Elastic net
so_fx.calculate_predictions(
    name="FX_EN",
    models=mods_fx_en,
    hparam_grid=grid_fx_en,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_EN", figsize=(18, 6))
display(som)

# Least squares
so_fx.calculate_predictions(
    name="FX_LS",
    models=mods_fx_ls,
    hparam_grid=grid_fx_ls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_LS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 242/242 [02:25<00:00,  1.67it/s]

None

100%|███████████████████████████████████████████████████████████████████████████████| 242/242 [00:02<00:00, 104.78it/s]

None

The view_timelines() method from the macrosynergy package displays both signals FX_EN and FX_LS :

sigs_fx_en = ["FX_EN", "FX_LS"]

xcatx = sigs_fx_en

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_fx_en = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs_fx_en,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_fx_en.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_EN	0.532	0.527	0.837	0.526	0.535	0.519	-0.023	0.086	0.003	0.762	0.515
FX_LS	0.528	0.518	0.665	0.537	0.549	0.487	0.025	0.068	0.026	0.004	0.516

sigs = sigs_fx_en

pnl_fx_en = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_fx_en.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_fx_en.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_fx_en.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_FX_EN	PNL_FX_LS
Return (pct ar)	0.626504	3.382204
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.06265	0.33822
Sortino Ratio	0.096964	0.46556
Max 21-day draw	-20.617232	-25.089697
Max 6-month draw	-24.605203	-23.025265
USD_EQXR_NSA correl	0.107473	0.094817
Traded Months	243	243

results_fx_en = msn.create_results_dataframe(
    title="Performance metrics, Elastic Net vs Least Squares, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_en,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_LS": "LS", "FX_EN": "EN"},
    slip=1,
    blacklist=fxblack,
)
results_fx_en

Performance metrics, Elastic Net vs Least Squares, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
EN	0.532	0.527	-0.023	0.003	0.063	0.097	0.107
LS	0.528	0.518	0.025	0.026	0.338	0.466	0.095

Comparison

In our data examples, elastic net on average produced signals with higher accuracy, but lower correlation and PnL performance ratios. For the duration and equity strategies the elastic produced very similar PnL profiles as OLS-based signals. However, the elastic net-based learning process “overregularized” features for the FX space and failed to produce non-zero signals prior to 2008 and after 2018.

The empirical analysis provides two important lessons:

• Elastic net may make excessive demands on financial return predictors. Regularized regressions that include a heavy L1 penalty can easily remove all features if they are sufficient in number and quality. And high predictive quality does not come easily for financial returns.

• Elastic net has a penchant for sporadic instability of signals. This arises from the greater number of hyperparameters that the statistical learning process can choose from. Hyperparameter instability is consequential for transaction costs and recorded signal-return correlation.

results_en = (results_du_en.data + results_eq_en.data + results_fx_en.data) / 3
results_en.style.format("{:.3f}").set_caption(
    "Averaged performance metrics, Elastic Net vs Least Squares"
).set_table_styles(
    [
        {
            "selector": "caption",
            "props": [("text-align", "center"), ("font-weight", "bold")],
        }
    ]
)

Averaged performance metrics, Elastic Net vs Least Squares

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
EN	0.544	0.524	0.030	0.025	0.369	0.512	0.251
LS	0.541	0.518	0.046	0.031	0.460	0.635	0.239

Time-weighted least squares

Weighted Least Squares (WLS) is form of generalized least squares that increases the importance of some samples relative to others. Time-Weighted Least Squares (TWLS) allows to prioritise more recent information in the model fit by defining a half-life of an exponential decay in units of the native dataset frequency. The half-life of the decay is one the hyperparameters which the learning process determines over time.

Duration

mods_du_twls = {
    "twls": msl.TimeWeightedLinearRegression(),
}

grid_du_twls = {
    "twls": {
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled DU_TWLS .

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)

# TWLS
so_du.calculate_predictions(
    name="DU_TWLS",
    models=mods_du_twls,
    hparam_grid=grid_du_twls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_TWLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 241/241 [00:21<00:00, 11.18it/s]

None

The view_timelines() method from the macrosynergy package displays both signals DU_TWLS and DU_LS .

sigs_du_twls = ["DU_TWLS", "DU_LS"]
xcatx = sigs_du_twls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_du_twls = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs_du_twls,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_du_twls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_TWLS	0.536	0.524	0.821	0.534	0.543	0.504	0.059	0.000	0.037	0.000	0.514
DU_LS	0.532	0.516	0.849	0.534	0.539	0.493	0.048	0.001	0.029	0.003	0.508

sigs = sigs_du_twls

pnl_du_twls = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_twls,
    cids=cids_dux,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_twls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_du_twls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_du_twls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_LS	PNL_DU_TWLS
Return (pct ar)	4.294597	5.216168
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.42946	0.521617
Sortino Ratio	0.594083	0.726427
Max 21-day draw	-24.904755	-21.490644
Max 6-month draw	-34.397224	-30.242448
USD_GB10YXR_NSA correl	0.450925	0.3709
Traded Months	242	242

results_du_twls = msn.create_results_dataframe(
    title="Performance metrics, LS vs TWLS, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_twls,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_GB10YXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_LS": "LS", "DU_TWLS": "TWLS"},
    slip=1,
    blacklist=fxblack,
)
results_du_twls

Performance metrics, LS vs TWLS, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.532	0.516	0.048	0.029	0.429	0.594	0.451
TWLS	0.536	0.524	0.059	0.037	0.522	0.726	0.371

Equity

mods_eq_twls = {
    "twls": msl.TimeWeightedLinearRegression(),
}

grid_eq_twls = {
    "twls": {
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled EQ_TWLS .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)

# TWLS
so_eq.calculate_predictions(
    name="EQ_TWLS",
    models=mods_eq_twls,
    hparam_grid=grid_eq_twls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_TWLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 245/245 [00:16<00:00, 15.04it/s]

None

The view_timelines() method from the macrosynergy package displays both signals EQ_TWLS and EQ_LS .

sigs_eq_twls = ["EQ_TWLS", "EQ_LS"]
xcatx = sigs_eq_twls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_eq_twls = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs_eq_twls,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_twls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_TWLS	0.577	0.535	0.701	0.619	0.640	0.430	0.066	0.004	0.040	0.009	0.531
EQ_LS	0.564	0.521	0.693	0.619	0.632	0.411	0.065	0.005	0.038	0.013	0.519

sigs = sigs_eq_twls

pnl_eq_twls = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cids_eq,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_eq_twls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_eq_twls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_eq_twls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_EQ_LS	PNL_EQ_TWLS
Return (pct ar)	6.125482	6.187539
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.612548	0.618754
Sortino Ratio	0.845046	0.853907
Max 21-day draw	-27.600217	-26.294693
Max 6-month draw	-19.515294	-18.076241
USD_EQXR_NSA correl	0.170386	0.164216
Traded Months	243	243

results_eq_twls = msn.create_results_dataframe(
    title="Performance metrics, LS vs TWLS, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_twls,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_LS": "LS", "EQ_TWLS": "TWLS"},
    slip=1,
)
results_eq_twls

Performance metrics, LS vs TWLS, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.564	0.521	0.065	0.038	0.613	0.845	0.170
TWLS	0.577	0.535	0.066	0.040	0.619	0.854	0.164

FX

mods_fx_twls = {
    "twls": msl.TimeWeightedLinearRegression(),
}

grid_fx_twls = {
    "twls": {
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled FX_TWLS .

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)

# TWLS
so_fx.calculate_predictions(
    name="FX_TWLS",
    models=mods_fx_twls,
    hparam_grid=grid_fx_twls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_TWLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 242/242 [00:24<00:00, 10.04it/s]

None

The view_timelines() method from the macrosynergy package displays both signals FX_TWLS and FX_LS .

sigs_fx_twls = ["FX_TWLS", "FX_LS"]
xcatx = sigs_fx_twls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_fx_twls = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs_fx_twls,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_fx_twls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_TWLS	0.520	0.508	0.676	0.537	0.542	0.473	0.030	0.030	0.024	0.007	0.507
FX_LS	0.528	0.518	0.665	0.537	0.549	0.487	0.025	0.068	0.026	0.004	0.516

sigs = sigs_fx_twls

pnl_fx_twls = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_fx_twls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_fx_twls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_fx_twls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_FX_LS	PNL_FX_TWLS
Return (pct ar)	3.382204	3.565424
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.33822	0.356542
Sortino Ratio	0.46556	0.49074
Max 21-day draw	-25.089697	-23.239084
Max 6-month draw	-23.025265	-21.619675
USD_EQXR_NSA correl	0.094817	0.092324
Traded Months	243	243

results_fx_twls = msn.create_results_dataframe(
    title="Performance metrics, LS vs TWLS, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_twls,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_LS": "LS", "FX_TWLS": "TWLS"},
    slip=1,
    blacklist=fxblack,
)
results_fx_twls

Performance metrics, LS vs TWLS, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.528	0.518	0.025	0.026	0.338	0.466	0.095
TWLS	0.520	0.508	0.030	0.024	0.357	0.491	0.092

Comparison

On average, the usage of time-weighted least squares in the learning process has produced modestly higher performance accuracy, correlation and PnL performance ratios.

There are a few important empirical lessons:

• The TWLS-based learning process tends to produce greater signal instability. Generally, the learning process with TWLS models likes to use constants more than the OLS/NNLS-based process. This seems to be another consequence of the focus on more recent history. Recent seasonality of returns or omitted explanatory variables result in better cross-validation results for models with constant. However, this way the TWLS constants become estimates of recent return trends, particularly if shorter half-lives are chosen.

• TWLS methods like non-negativity restrictions: Time-weighted least squares almost exclusively uses non-negative least squares. The behaviour of hyperparameter optimization is line with theory: shorter effective lookback periods call for more restrictions as the bias-variance trade-off is quite poor.

results_twls = (results_du_twls.data + results_eq_twls.data + results_fx_twls.data) / 3
results_twls.style.format("{:.3f}").set_caption(
    "Averaged performance metrics, LS vs TWLS"
).set_table_styles(
    [
        {
            "selector": "caption",
            "props": [("text-align", "center"), ("font-weight", "bold")],
        }
    ]
)

Averaged performance metrics, LS vs TWLS

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.541	0.518	0.046	0.031	0.460	0.635	0.239
TWLS	0.544	0.522	0.052	0.034	0.499	0.690	0.209

Sign-weighted least squares

Sign-weighted least squares (SWLS) equalises the contribution of positive and negative samples to the model fit. If, for example, returns are predominantly positive then historic observations with negative target returns are assigned higher weights that those with negative returns. This mitigates the directional bias in general and largely removes any bias that manifests through the recession constant.

Duration

mods_du_swls = {
    "swls": msl.SignWeightedLinearRegression(),
}

grid_du_swls = {
    "swls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
}

As previously, SignalOptimizer class for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled DU_SWLS

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)
so_du.calculate_predictions(
    name="DU_SWLS",
    models=mods_du_swls,
    hparam_grid=grid_du_swls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_SWLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 241/241 [00:02<00:00, 110.76it/s]

None

The view_timelines() method from the macrosynergy package displays both signals DU_SWLS and DU_LS .

sigs_du_swls = ["DU_SWLS", "DU_LS"]
xcatx = sigs_du_swls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_du_swls = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs_du_swls,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_du_swls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_SWLS	0.533	0.525	0.635	0.534	0.553	0.497	0.055	0.000	0.036	0.000	0.523
DU_LS	0.532	0.516	0.849	0.534	0.539	0.493	0.048	0.001	0.029	0.003	0.508

sigs = sigs_du_swls

pnl_du_swls = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs,
    cids=cids_dux,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_swls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_du_swls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_du_swls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_LS	PNL_DU_SWLS
Return (pct ar)	4.294597	5.959713
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.42946	0.595971
Sortino Ratio	0.594083	0.854025
Max 21-day draw	-24.904755	-18.295261
Max 6-month draw	-34.397224	-26.078981
USD_GB10YXR_NSA correl	0.450925	0.196792
Traded Months	242	242

results_du_swls = msn.create_results_dataframe(
    title="Performance metrics, LS vs SWLS, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_swls,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_GB10YXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_LS": "LS", "DU_SWLS": "SWLS"},
    slip=1,
    blacklist=fxblack,
)
results_du_swls

Performance metrics, LS vs SWLS, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.532	0.516	0.048	0.029	0.429	0.594	0.451
SWLS	0.533	0.525	0.055	0.036	0.596	0.854	0.197

Equity

mods_eq_swls = {
    "swls": msl.SignWeightedLinearRegression(),
}

grid_eq_swls = {
    "swls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled EQ_SWLS .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)
so_eq.calculate_predictions(
    name="EQ_SWLS",
    models=mods_eq_swls,
    hparam_grid=grid_eq_swls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_SWLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 245/245 [00:01<00:00, 122.67it/s]

None

The view_timelines() method from the macrosynergy package displays both signals EQ_SWLS and EQ_LS .

sigs_eq_swls = ["EQ_SWLS", "EQ_LS"]
xcatx = sigs_eq_swls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_eq_swls = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs_eq_swls,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_swls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_SWLS	0.561	0.527	0.653	0.619	0.638	0.416	0.072	0.002	0.047	0.002	0.526
EQ_LS	0.564	0.521	0.693	0.619	0.632	0.411	0.065	0.005	0.038	0.013	0.519

sigs = sigs_eq_swls

pnl_eq_swls = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cids_eq,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)

for sig in sigs:
    pnl_eq_swls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_eq_swls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_eq_swls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_EQ_LS	PNL_EQ_SWLS
Return (pct ar)	6.125482	5.915155
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.612548	0.591516
Sortino Ratio	0.845046	0.825849
Max 21-day draw	-27.600217	-16.559704
Max 6-month draw	-19.515294	-16.891076
USD_EQXR_NSA correl	0.170386	0.086166
Traded Months	243	243

results_eq_swls = msn.create_results_dataframe(
    title="Performance metrics, LS vs SWLS, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_swls,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_LS": "LS", "EQ_SWLS": "SWLS"},
    slip=1,
)
results_eq_swls

Performance metrics, LS vs SWLS, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.564	0.521	0.065	0.038	0.613	0.845	0.170
SWLS	0.561	0.527	0.072	0.047	0.592	0.826	0.086

FX

mods_fx_swls = {
    "swls": msl.SignWeightedLinearRegression(),
}

grid_fx_swls = {
    "swls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled FX_SWLS

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)
so_fx.calculate_predictions(
    name="FX_SWLS",
    models=mods_fx_swls,
    hparam_grid=grid_fx_swls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_SWLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|███████████████████████████████████████████████████████████████████████████████| 242/242 [00:02<00:00, 106.74it/s]

None

The view_timelines() method from the macrosynergy package displays both signals FX_SWLS and FX_LS .

sigs_fx_swls = ["FX_SWLS", "FX_LS"]
xcatx = sigs_fx_swls

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_fx_swls = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs_fx_swls,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_fx_swls.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_SWLS	0.508	0.506	0.531	0.537	0.542	0.469	0.017	0.206	0.016	0.070	0.506
FX_LS	0.528	0.518	0.665	0.537	0.549	0.487	0.025	0.068	0.026	0.004	0.516

sigs = sigs_fx_swls

pnl_fx_swls = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_fx_swls.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )
pnl_fx_swls.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_fx_swls.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_FX_LS	PNL_FX_SWLS
Return (pct ar)	3.382204	2.701333
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.33822	0.270133
Sortino Ratio	0.46556	0.38021
Max 21-day draw	-25.089697	-20.540039
Max 6-month draw	-23.025265	-41.439155
USD_EQXR_NSA correl	0.094817	-0.126136
Traded Months	243	243

results_fx_swls = msn.create_results_dataframe(
    title="Performance metrics, LS vs SWLS, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_swls,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_LS": "LS", "FX_SWLS": "SWLS"},
    slip=1,
    blacklist=fxblack,
)
results_fx_swls

Performance metrics, LS vs SWLS, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.528	0.518	0.025	0.026	0.338	0.466	0.095
SWLS	0.508	0.506	0.017	0.016	0.270	0.380	-0.126

Comparison

On average across the strategies of the analysis, statistical learning with sign-weighted least squares produces slightly higher correlation and PnL performance ratios than least squares. Importantly, the average benchmark correlation of strategies has been very low (around 5%) versus 25% for the least squares-based signal.

The main empirical lessons reflect the purpose of SWLS:

• SWLS-based learning reduces directional bias. Since the method weighs positive and negative return experiences equally, all directional bias arises from seasonality of returns (equity market boom) or the omittion of a variable such as a long-term premium. This is echoed by the removal of the long bias across all our sample strategies. Such a complete removal is desirable if the experiences of (rarer) negative return periods are truly more valuable as positive return periods.

• SWLS likes to work with non-negativity restrictions: In our examples, SWLS learning would have always chosen models with non-negative coefficient restrictions. This may be a sign of suitability for the implementation of theoretical priors across different asset return seasons.

results_swls = (results_du_swls.data + results_eq_swls.data + results_fx_swls.data) / 3
results_swls.style.format("{:.3f}").set_caption(
    "Averaged performance metrics, LS vs SWLS"
).set_table_styles(
    [
        {
            "selector": "caption",
            "props": [("text-align", "center"), ("font-weight", "bold")],
        }
    ]
)

Averaged performance metrics, LS vs SWLS

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LS	0.541	0.518	0.046	0.031	0.460	0.635	0.239
SWLS	0.534	0.519	0.048	0.033	0.486	0.687	0.052

Least absolute deviations

LAD regression is median regression, i.e., special case of quantile regression. It is a robust regression method that is less sensitive to outliers than standard least squares regression. Least squares can compromise the message of the many for the sake a few, specifically extreme values. LAD mitigates this issue by using absolute values of errors, rather than their squares.

Duration

# All WLAD regressors (Weighted LAD)
mods_du_wlad = {
    "lad": msl.LADRegressor(),
    "swlad": msl.SignWeightedLADRegressor(),
    "twlad": msl.TimeWeightedLADRegressor(),
}

grid_du_wlad = {
    "lad": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
    "swlad": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
    "twlad": {
        "positive": [True, False],
        "fit_intercept": [True, False],
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
    },
}

# All WLS regressors (Weighted LS)
mods_du_wls = {
    "ols": LinearRegression(),
    "swls": msl.SignWeightedLinearRegression(),
    "twls": msl.TimeWeightedLinearRegression(),
}

grid_du_wls = {
    "ols": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
    "swls": {
        "positive": [True, False],
        "fit_intercept": [True, False],
    },
    "twls": {
        "positive": [True, False],
        "fit_intercept": [True, False],
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled DU_WLAD .

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)

# WLAD
so_du.calculate_predictions(
    name="DU_WLAD",
    models=mods_du_wlad,
    hparam_grid=grid_du_wlad,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_WLAD", figsize=(18, 6))
display(som)

# WLS
so_du.calculate_predictions(
    name="DU_WLS",
    models=mods_du_wls,
    hparam_grid=grid_du_wls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_WLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 241/241 [06:21<00:00,  1.58s/it]

None

100%|████████████████████████████████████████████████████████████████████████████████| 241/241 [00:29<00:00,  8.17it/s]

None

The view_timelines() method from the macrosynergy package displays both signals DU_WLAD and DU_WLS .

sigs_du_lad = ["DU_WLAD", "DU_WLS"]
xcatx = sigs_du_lad

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_du_lad = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs_du_lad,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_du_lad.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_WLAD	0.527	0.503	0.872	0.534	0.535	0.471	0.039	0.008	0.025	0.009	0.501
DU_WLS	0.532	0.515	0.851	0.534	0.539	0.491	0.050	0.001	0.031	0.001	0.508

sigs = sigs_du_lad

pnl_du_lad = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs,
    cids=cids_dux,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_lad.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_du_lad.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_du_lad.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_WLAD	PNL_DU_WLS
Return (pct ar)	3.841205	4.599956
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.38412	0.459996
Sortino Ratio	0.533189	0.640593
Max 21-day draw	-22.488852	-22.171126
Max 6-month draw	-34.189256	-31.223396
USD_GB10YXR_NSA correl	0.462098	0.446181
Traded Months	242	242

results_du_lad = msn.create_results_dataframe(
    title="Performance metrics, LAD vs LS, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_lad,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_WLS": "LS", "DU_WLAD": "LAD"},
    slip=1,
    blacklist=fxblack,
)
results_du_lad

Performance metrics, LAD vs LS, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LAD	0.527	0.503	0.039	0.025	0.384	0.533	-0.124
LS	0.532	0.515	0.050	0.031	0.460	0.641	-0.132

Equity

# All WLAD regressors (Weighted LAD)
mods_eq_wlad = {
    "lad": msl.LADRegressor(),
    "swlad": msl.SignWeightedLADRegressor(),
    "twlad": msl.TimeWeightedLADRegressor(),
}

grid_eq_wlad = {
    "lad": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "swlad": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "twlad": {
        "fit_intercept": [True, False],
        "positive": [True, False],
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
    },
}

# All WLS regressors (Weighted LS)
mods_eq_wls = {
    "ols": LinearRegression(),
    "swls": msl.SignWeightedLinearRegression(),
    "twls": msl.TimeWeightedLinearRegression(),
}

grid_eq_wls = {
    "ols": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "swls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "twls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
        "half_life": [
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled EQ_WLAD .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)

# WLAD
so_eq.calculate_predictions(
    name="EQ_WLAD",
    models=mods_eq_wlad,
    hparam_grid=grid_eq_wlad,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_WLAD", figsize=(18, 6))
display(som)

# WLS
so_eq.calculate_predictions(
    name="EQ_WLS",
    models=mods_eq_wls,
    hparam_grid=grid_eq_wls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_WLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 245/245 [06:08<00:00,  1.50s/it]

None

100%|████████████████████████████████████████████████████████████████████████████████| 245/245 [00:23<00:00, 10.59it/s]

None

The view_timelines() function from the macrosynergy package displays both signals EQ_WLAD and EQ_WLS .

sigs_eq_lad = ["EQ_WLAD", "EQ_WLS"]
xcatx = sigs_eq_lad

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_eq_lad = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs_eq_lad,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_lad.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_WLAD	0.575	0.538	0.675	0.619	0.644	0.432	0.058	0.012	0.037	0.015	0.536
EQ_WLS	0.566	0.524	0.691	0.619	0.634	0.415	0.063	0.006	0.037	0.014	0.522

sigs = sigs_eq_lad

pnl_eq_lad = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cids_eq,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_eq_lad.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_eq_lad.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_eq_lad.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_EQ_WLAD	PNL_EQ_WLS
Return (pct ar)	5.74141	5.962238
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.574141	0.596224
Sortino Ratio	0.787544	0.821435
Max 21-day draw	-30.200681	-27.718885
Max 6-month draw	-21.077694	-19.446972
USD_EQXR_NSA correl	0.182025	0.161229
Traded Months	243	243

results_eq_lad = msn.create_results_dataframe(
    title="Performance metrics, LAD vs LS, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_lad,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_WLS": "LS", "EQ_WLAD": "LAD"},
    slip=1,
)
results_eq_lad

Performance metrics, LAD vs LS, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LAD	0.575	0.538	0.058	0.037	0.574	0.788	0.182
LS	0.566	0.524	0.063	0.037	0.596	0.821	0.161

FX

# All WLAD regressors
mods_fx_wlad = {
    "lad": msl.LADRegressor(),
    "swlad": msl.SignWeightedLADRegressor(),
    "twlad": msl.TimeWeightedLADRegressor(),
}

grid_fx_wlad = {
    "lad": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "swlad": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "twlad": {
        "fit_intercept": [True, False],
        "positive": [True, False],
        "half_life": [
            12 * 0.5,
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
    },
}

# All WLS regressors (Weighted LS)
mods_fx_wls = {
    "ols": LinearRegression(),
    "swls": msl.SignWeightedLinearRegression(),
    "twls": msl.TimeWeightedLinearRegression(),
}

grid_fx_wls = {
    "ols": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "swls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
    },
    "twls": {
        "fit_intercept": [True, False],
        "positive": [True, False],
        "half_life": [
            12 * 0.5,
            12 * 1,
            12 * 3,
            12 * 5,
            12 * 10,
            12 * 20,
        ],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled FX_WLAD .

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)

# WLAD
so_fx.calculate_predictions(
    name="FX_WLAD",
    models=mods_fx_wlad,
    hparam_grid=grid_fx_wlad,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_WLAD", figsize=(18, 6))
display(som)

# WLS
so_fx.calculate_predictions(
    name="FX_WLS",
    models=mods_fx_wls,
    hparam_grid=grid_fx_wls,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_WLS", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 242/242 [08:14<00:00,  2.04s/it]

None

100%|████████████████████████████████████████████████████████████████████████████████| 242/242 [00:36<00:00,  6.57it/s]

None

The view_timelines() method from the macrosynergy package displays both signals FX_WLAD and FX_WLS .

sigs_fx_lad = ["FX_WLAD", "FX_WLS"]
xcatx = sigs_fx_lad

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores

srr_fx_lad = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs_fx_lad,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_fx_lad.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_WLAD	0.530	0.518	0.702	0.537	0.548	0.488	0.022	0.108	0.024	0.008	0.515
FX_WLS	0.525	0.515	0.665	0.537	0.547	0.483	0.032	0.018	0.027	0.003	0.513

sigs = sigs_fx_lad

pnl_fx_lad = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
    blacklist=fxblack,
)
for sig in sigs:
    pnl_fx_lad.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_fx_lad.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_fx_lad.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_FX_WLAD	PNL_FX_WLS
Return (pct ar)	3.192739	4.011113
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.319274	0.401111
Sortino Ratio	0.436716	0.556909
Max 21-day draw	-23.893715	-23.36819
Max 6-month draw	-24.690872	-21.909655
USD_EQXR_NSA correl	0.109705	0.053612
Traded Months	243	243

results_fx_lad = msn.create_results_dataframe(
    title="Performance metrics, LAD vs LS, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_lad,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_WLS": "LS", "FX_WLAD": "LAD"},
    slip=1,
    blacklist=fxblack,
)
results_fx_lad

Performance metrics, LAD vs LS, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LAD	0.530	0.518	0.022	0.024	0.319	0.437	0.110
LS	0.525	0.515	0.032	0.027	0.401	0.557	0.054

Comparison

LAD regression does not generally improve signal quality. Average accuracy and balanced accuracy for our strategy types have been higher than for least squares, but correlation and portfolio performance ratios have been smaller.

Two important empirical lessons:

• LAD is not generally a game changer for macro signals: Even though economic data and financial returns are prone to outliers these are often not large enough to bring out the full benefits of the LAD approach. This may reflect that with the low average explanatory power of features with respect to future financial returns, regressions rarely produce large coefficients in the first place and the main job of the regression is really selecting features and weighing them relative to each other.

• LAD also likes to work with non-negativity restrictions: For all strategies the most frequently chosen LAD and LS versions use the non-negative coefficient restrictions. This is a reminder of the benefits of theoretical priors, at least in respect to direction of feature impact.

results_lad = (results_du_lad.data + results_eq_lad.data + results_fx_lad.data) / 3
results_lad.style.format("{:.3f}").set_caption(
    "Averaged performance metrics, LAD vs LS"
).set_table_styles(
    [
        {
            "selector": "caption",
            "props": [("text-align", "center"), ("font-weight", "bold")],
        }
    ]
)

Averaged performance metrics, LAD vs LS

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
LAD	0.544	0.520	0.040	0.029	0.426	0.586	0.056
LS	0.541	0.518	0.048	0.032	0.486	0.673	0.028

KNN

All above models are linear and parametric. The KNN class of models makes predictions by averaging the nearest \(k\) training samples, possibly taking a weighted average based on sample distance. In this context, this leads to return prediction based on the most similar feature constellations of the past. In the concept of macro signals, this reduces theoretical priors (and probably enhances model variance) for the sake of less model bias.

Duration

mods_du_knn = {
    "knn": KNeighborsRegressor(),
}

grid_du_knn = {
    "knn": {
        "n_neighbors": [i for i in range(1, 105, 5)],
        "weights": ["uniform", "distance"],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_du , and the targets in y_du , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled DU_KNN .

so_du = msl.SignalOptimizer(inner_splitter=splitter, X=X_du, y=y_du, blacklist=fxblack)

# KNN
so_du.calculate_predictions(
    name="DU_KNN",
    models=mods_du_knn,
    hparam_grid=grid_du_knn,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_du.models_heatmap(name="DU_KNN", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_du.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 241/241 [01:12<00:00,  3.34it/s]

None

The view_timelines() method from the macrosynergy package displays both signals DU_KNN and DU_LS .

sigs_du_knn = ["DU_KNN", "DU_LS"]
xcatx = sigs_du_knn

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_dux,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores
sigs = sigs_du_knn

srr_du_knn = mss.SignalReturnRelations(
    df=dfx,
    rets=["DU05YXR_VT10"],
    sigs=sigs,
    cids=cids_dux,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_du_knn.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
DU_KNN	0.528	0.513	0.774	0.534	0.540	0.486	0.034	0.020	0.017	0.089	0.509
DU_LS	0.532	0.516	0.849	0.534	0.539	0.493	0.048	0.001	0.029	0.003	0.508

pnl_du_knn = msn.NaivePnL(
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs,
    cids=cids_dux,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_GB10YXR_NSA"],
)
for sig in sigs:
    pnl_du_knn.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_du_knn.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_du_knn.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

xcat	PNL_DU_KNN	PNL_DU_LS
Return (pct ar)	3.836123	4.294597
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.383612	0.42946
Sortino Ratio	0.528405	0.594083
Max 21-day draw	-26.781588	-24.904755
Max 6-month draw	-35.346306	-34.397224
USD_GB10YXR_NSA correl	0.313037	0.450925
Traded Months	242	242

results_du_knn = msn.create_results_dataframe(
    title="Performance metrics, KNN vs LS, duration",
    df=dfx,
    ret="DU05YXR_VT10",
    sigs=sigs_du_knn,
    cids=cids_dux,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_GB10YXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"DU_LS": "LS", "DU_KNN": "KNN"},
    slip=1,
    blacklist=fxblack,
)
results_du_knn

Performance metrics, KNN vs LS, duration

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
KNN	0.528	0.513	0.034	0.017	0.384	0.528	0.313
LS	0.532	0.516	0.048	0.029	0.429	0.594	0.451

Equity

mods_eq_knn = {
    "knn": KNeighborsRegressor(),
}

grid_eq_knn = {
    "knn": {
        "n_neighbors": [i for i in range(1, 101, 5)],
        "weights": ["uniform", "distance"],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_eq , and the targets in y_eq , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled EQ_KNN .

so_eq = msl.SignalOptimizer(inner_splitter=splitter, X=X_eq, y=y_eq)
so_eq.calculate_predictions(
    name="EQ_KNN",
    models=mods_eq_knn,
    hparam_grid=grid_eq_knn,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_eq.models_heatmap(name="EQ_KNN", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_eq.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 245/245 [00:38<00:00,  6.35it/s]

None

The view_timelines() method from the macrosynergy package displays both signals EQ_KNN and EQ_LS .

sigs_eq_knn = ["EQ_KNN", "EQ_LS"]
xcatx = sigs_eq_knn

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_eq,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores
sigs = sigs_eq_knn

srr_eq_knn = mss.SignalReturnRelations(
    df=dfx,
    rets=["EQXR_VT10"],
    sigs=sigs,
    cids=cids_eq,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
)

srr_eq_knn.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
EQ_KNN	0.580	0.520	0.779	0.619	0.628	0.411	0.015	0.515	0.006	0.709	0.514
EQ_LS	0.564	0.521	0.693	0.619	0.632	0.411	0.065	0.005	0.038	0.013	0.519

pnl_eq_knn = msn.NaivePnL(
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs,
    cids=cids_eq,
    start="2004-01-01",
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_eq_knn.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_eq_knn.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_eq_knn.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

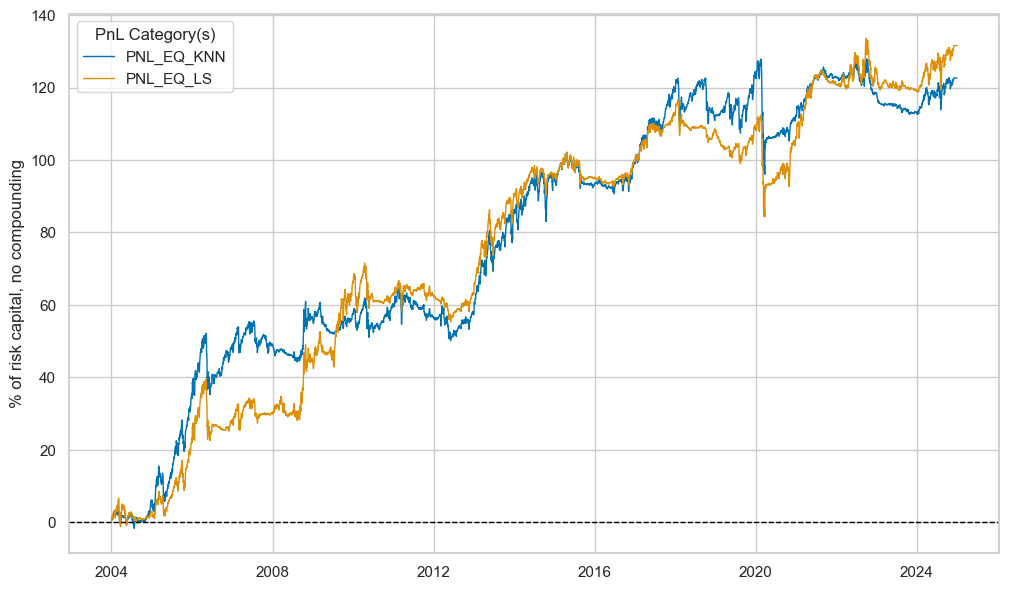
xcat	PNL_EQ_KNN	PNL_EQ_LS
Return (pct ar)	5.558221	6.125482
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.555822	0.612548
Sortino Ratio	0.753212	0.845046
Max 21-day draw	-30.373162	-27.600217
Max 6-month draw	-20.355528	-19.515294
USD_EQXR_NSA correl	0.262779	0.170386
Traded Months	243	243

results_eq_knn = msn.create_results_dataframe(
    title="Performance metrics, KNN vs LS, equity",
    df=dfx,
    ret="EQXR_VT10",
    sigs=sigs_eq_knn,
    cids=cids_eq,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"EQ_LS": "LS", "EQ_KNN": "KNN"},
    slip=1,
)
results_eq_knn

Performance metrics, KNN vs LS, equity

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
KNN	0.580	0.520	0.015	0.006	0.556	0.753	0.263
LS	0.564	0.521	0.065	0.038	0.613	0.845	0.170

FX

mods_fx_knn = {
    "knn": KNeighborsRegressor(),
}

grid_fx_knn = {
    "knn": {
        "n_neighbors": [i for i in range(1, 105, 5)],
        "weights": ["uniform", "distance"],
    },
}

As previously, the SignalOptimizer class allows for sequential optimization of raw signals based on quantamental features. The features are lagged quantamental indicators, collected in the dataframe X_fx , and the targets in y_fx , are cumulative returns at the native frequency. Please read here for detailed descriptions and examples. The derived signal is labeled FX_KNN .

so_fx = msl.SignalOptimizer(inner_splitter=splitter, X=X_fx, y=y_fx, blacklist=fxblack)
so_fx.calculate_predictions(
    name="FX_KNN",
    models=mods_fx_knn,
    hparam_grid=grid_fx_knn,
    metric=scorer,
    min_cids=4,
    min_periods=36,
)

som = so_fx.models_heatmap(name="FX_KNN", figsize=(18, 6))
display(som)

# Get optimized signals
dfa = so_fx.get_optimized_signals()

dfx = msm.update_df(dfx, dfa)

100%|████████████████████████████████████████████████████████████████████████████████| 242/242 [01:59<00:00,  2.03it/s]

None

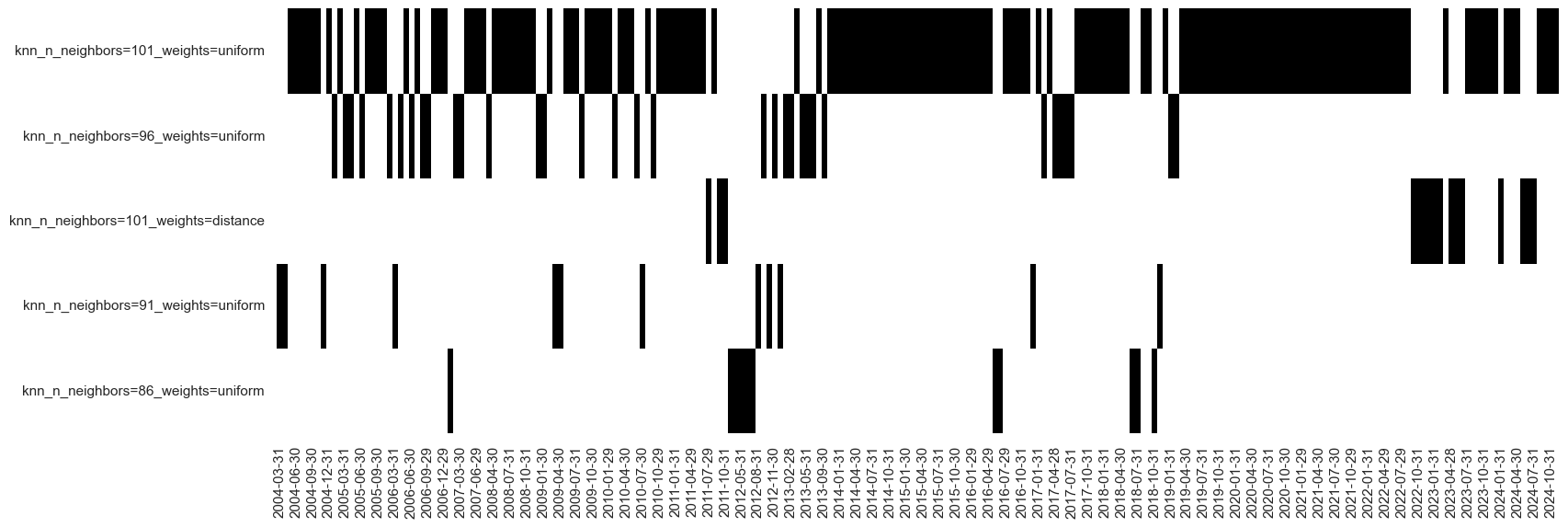
The view_timelines() method from the macrosynergy package displays both signals FX_KNN and FX_LS .

sigs_fx_knn = ["FX_KNN", "FX_LS"]
xcatx = sigs_fx_knn

msp.view_timelines(
    dfx,
    xcats=xcatx,
    cids=cids_fx,
    ncol=4,
    start="2004-01-01",
    title=None,
    title_fontsize=30,
    same_y=False,
    cs_mean=False,
    xcat_labels=None,
    legend_fontsize=16,
)

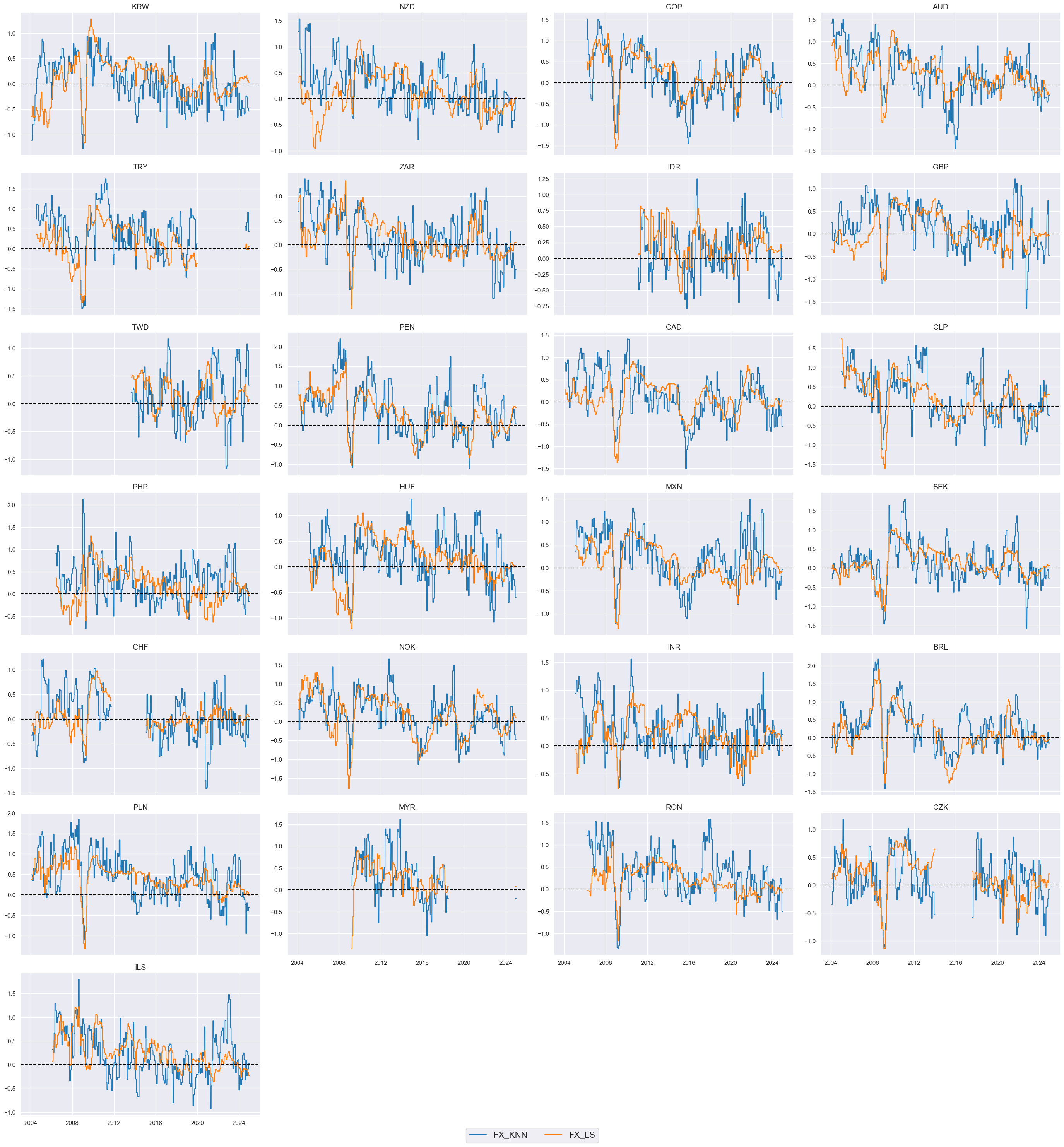
Value checks

The SignalReturnRelations class of the macrosynergy package facilitates a quick assessment of the power of a signal category in predicting the direction of subsequent returns for data in JPMaQS format.

The NaivePnl() class is specifically designed to offer a quick and straightforward overview of a simplified Profit and Loss (PnL) profile associated with a set of trading signals. The term “naive” is used because the methods within this class do not factor in transaction costs or position limitations, which may include considerations related to risk management. This omission is intentional because the impact of costs and limitations varies widely depending on factors such as trading size, institutional rules, and regulatory requirements.

For a comparative overview of the signal-return relationship across both signals, one can use the signals_table() method.

## Compare optimized signals with simple average z-scores
sigs = sigs_fx_knn

srr_fx_knn = mss.SignalReturnRelations(
    df=dfx,
    rets=["FXXR_VT10"],
    sigs=sigs,
    cids=cids_fx,
    cosp=True,
    freqs=["M"],
    agg_sigs=["last"],
    start="2004-01-01",
    slip=1,
    blacklist=fxblack,
)

srr_fx_knn.signals_table().astype("float").round(3)

	accuracy	bal_accuracy	pos_sigr	pos_retr	pos_prec	neg_prec	pearson	pearson_pval	kendall	kendall_pval	auc
FX_KNN	0.522	0.510	0.683	0.537	0.543	0.476	0.022	0.102	0.018	0.053	0.508
FX_LS	0.528	0.518	0.665	0.537	0.549	0.487	0.025	0.068	0.026	0.004	0.516

pnl_fx_knn = msn.NaivePnL(
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs,
    cids=cids_fx,
    start="2004-01-01",
    blacklist=fxblack,
    bms=["USD_EQXR_NSA"],
)
for sig in sigs:
    pnl_fx_knn.make_pnl(
        sig=sig,
        sig_op="zn_score_pan",
        rebal_freq="monthly",
        neutral="zero",
        rebal_slip=1,
        vol_scale=10,
        thresh=2,
    )

pnl_fx_knn.plot_pnls(
    title=None,
    title_fontsize=14,
    xcat_labels=None,
)

pnl_fx_knn.evaluate_pnls(pnl_cats=["PNL_" + sig for sig in sigs])

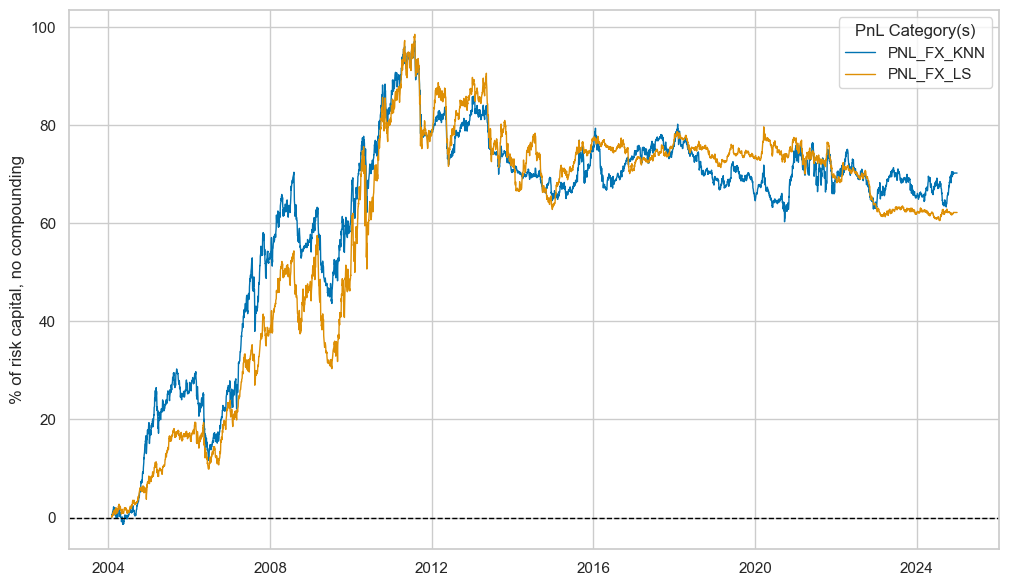
xcat	PNL_FX_KNN	PNL_FX_LS
Return (pct ar)	2.983802	3.382204
St. Dev. (pct ar)	10.0	10.0
Sharpe Ratio	0.29838	0.33822
Sortino Ratio	0.406634	0.46556
Max 21-day draw	-15.827396	-25.089697
Max 6-month draw	-16.984662	-23.025265
USD_EQXR_NSA correl	0.151945	0.094817
Traded Months	243	243

results_fx_knn = msn.create_results_dataframe(
    title="Performance metrics, KNN vs LS, FX",
    df=dfx,
    ret="FXXR_VT10",
    sigs=sigs_fx_knn,
    cids=cids_fx,
    sig_ops="zn_score_pan",
    sig_adds=0,
    neutrals="zero",
    threshs=2,
    bm="USD_EQXR_NSA",
    cosp=True,
    start="2004-01-01",
    freqs="M",
    agg_sigs="last",
    sigs_renamed={"FX_LS": "LS", "FX_KNN": "KNN"},
    slip=1,
    blacklist=fxblack,
)
results_fx_knn

Performance metrics, KNN vs LS, FX

	Accuracy	Bal. Accuracy	Pearson	Kendall	Sharpe	Sortino	Market corr.
KNN	0.522	0.510	0.022	0.018	0.298	0.407	0.152
LS	0.528	0.518	0.025	0.026	0.338	0.466	0.095

Comparison

Signals of KNN-based learning are very different from the least squares-based signals. Average performance metrics are worse than for least squares-based signals.

• KNN is for the case of few theoretical clues: KNN-based learning operates with little theory and restrictions: Moreover, key hyperparameters, such as the number of neighbours, lack clear theoretical guidance. This explains why its regression signals are more at the mercy of past experiences and optimal model is changing often.

• Good fea