Construction activity surprises #
This category group contains economic surprise indicators related to construction activity. At present they cover only survey data. Economic surprises are deviations of point-in-time quantamental indicators from predicted values. For an in-depth explanation, please read Appendix 2 .
Construction survey score surprises #
Ticker : CBCSCORE_SA_ARMAS / _3MMA_ARMAS
Label : Construction confidence score, ARMA(1,1)-based surprises: z-score, sa / z-score, sa, 3mma
Definition : Construction confidence score, ARMA(1,1)-based surprises: seasonally adjusted / seasonally adjusted , 3-month moving average
Notes :
-
Refer to the section on construction survey scores for notes on the underlying data series.
-
Expected values for release dates are based on an “ARMA(1,1)” model. This is a simple univariate time series model that predicts increments based on an autoregressive component, i.e., last period’s value, and a moving average component, represented by last period’s error. The coefficients of the model are estimated sequentially based on the vintages of production indices. And each vintage-specific model produces a one-step-ahead forecast for the subsequent observation period.
Ticker : CBCSCORE_SA_D1M1ML1_ARMAS / _D3M3ML3_ARMAS / _D1Q1QL1_ARMAS / _D6M6ML6_ARMAS / _D2Q2QL2_ARMAS / _D1M1ML12_ARMAS / _3MMA_D1M1ML12_ARMAS / _D1Q1QL4_ARMAS
Label : Construction confidence change, sa, , ARMA(1,1)-based surprises: diff m/m / diff 3m/3m / diff q/q / diff 6m/6m / diff 2q/2q / diff oya (m) / diff oya, 3mma / diff oya (q)
Definition : Construction confidence change, seasonally adjusted, ARMA(1,1)-based surprises: difference over 1 month / difference of last 3 months over previous 3 months / difference of last quarter over previous quarter / difference of last 6 months over previous 6 months / difference of last 2 quarters over previous 2 quarters / difference over a year ago, monthly values / difference over a year ago, 3-month moving average / difference over a year ago, quarterly values
Notes :
-
Refer to the section on construction survey scores for notes on the underlying data series.
-
Expected values for release dates are based on an “ARMA(1,1)” model. This is a simple univariate time series model that predicts increments based on an autoregressive component, i.e., last period’s value, and a moving average component, represented by last period’s error. The coefficients of the model are estimated sequentially based on the vintages of production indices. And each vintage-specific model produces a one-step-ahead forecast for the subsequent observation period.
Imports #
Only the standard Python data science packages and the specialized
macrosynergy
package are needed.
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math
import json
import yaml
import macrosynergy.management as msm
import macrosynergy.panel as msp
import macrosynergy.signal as mss
import macrosynergy.pnl as msn
import macrosynergy.visuals as msv
from macrosynergy.download import JPMaQSDownload
from timeit import default_timer as timer
from datetime import timedelta, date, datetime
import warnings
warnings.simplefilter("ignore")
The
JPMaQS
indicators we consider are downloaded using the J.P. Morgan Dataquery API interface within the
macrosynergy
package. This is done by specifying
ticker strings
, formed by appending an indicator category code
<category>
to a currency area code
<cross_section>
. These constitute the main part of a full quantamental indicator ticker, taking the form
DB(JPMAQS,<cross_section>_<category>,<info>)
, where
<info>
denotes the time series of information for the given cross-section and category. The following types of information are available:
-
valuegiving the latest available values for the indicator -
eop_lagreferring to days elapsed since the end of the observation period -
mop_lagreferring to the number of days elapsed since the mean observation period -
gradedenoting a grade of the observation, giving a metric of real time information quality.
After instantiating the
JPMaQSDownload
class within the
macrosynergy.download
module, one can use the
download(tickers,start_date,metrics)
method to easily download the necessary data, where
tickers
is an array of ticker strings,
start_date
is the first collection date to be considered and
metrics
is an array comprising the times series information to be downloaded.
cids_dmca = [
"AUD",
"CAD",
"CHF",
"EUR",
"GBP",
"JPY",
"NOK",
"NZD",
"SEK",
"USD",
] # DM currency areas
cids_dmec = ["DEM", "ESP", "FRF", "ITL", "NLG"] # DM euro area countries
cids_latm = ["BRL", "COP", "CLP", "MXN", "PEN"] # Latam countries
cids_emea = ["CZK", "HUF", "ILS", "PLN", "RON", "RUB", "TRY", "ZAR"] # EMEA countries
cids_emas = [
"CNY",
"HKD",
"IDR",
"INR",
"KRW",
"MYR",
"PHP",
"SGD",
"THB",
"TWD",
] # EM Asia countries
cids_dm = cids_dmca + cids_dmec
cids_em = cids_latm + cids_emea + cids_emas
cids = sorted(cids_dm + cids_em)
# FX cross-sections lists (for research purposes)
cids_nofx = ["EUR", "USD", "SGD"] + cids_dmec
cids_fx = list(set(cids) - set(cids_nofx))
cids_dmfx = set(cids_dm).intersection(cids_fx)
cids_emfx = set(cids_em).intersection(cids_fx)
cids_eur = ["CHF", "CZK", "HUF", "NOK", "PLN", "RON", "SEK"] # trading against EUR
cids_eud = ["GBP", "RUB", "TRY"] # trading against EUR and USD
cids_usd = list(set(cids_fx) - set(cids_eur + cids_eud))
cstr_conf = [
# CONFIDENCE
f"CBCSCORE_SA{transformation:s}{model:s}"
for transformation in ("", "_3MMA", "_D1M1ML1", "_D3M3ML3", "_D1Q1QL1", "_D6M6ML6", "_D2Q2QL2", "_3MMA_D1M1ML12", "_D1M1ML12", "_D1Q1QL4")
for model in ["_ARMAS"]
]
main = cstr_conf
econ = ["USDGDPWGT_SA_1YMA", "IVAWGT_SA_1YMA"] # economic context
mark = [
"DU02YXR_NSA",
"DU05YXR_NSA",
"DU02YXR_VT10",
"DU05YXR_VT10",
"CDS02YXR_VT10",
"CDS05YXR_VT10",
"FXXR_NSA",
"FXTARGETED_NSA",
"FXUNTRADABLE_NSA",
] # market links
xcats = main + econ + mark
cids_co = [
"ALM",
"CPR",
"ZNC",
]
xcats_co = ["COXR_NSA", "COXR_VT10"]
cotix = [cid + "_" + xcat for cid in cids_co for xcat in xcats_co]
# Download series from J.P. Morgan DataQuery by tickers
start_date = "1990-01-01"
tickers = [cid + "_" + xcat for cid in cids for xcat in xcats] +cotix
print(f"Maximum number of tickers is {len(tickers)}")
# Retrieve credentials
client_id: str = os.getenv("DQ_CLIENT_ID")
client_secret: str = os.getenv("DQ_CLIENT_SECRET")
# Download from DataQuery
with JPMaQSDownload(client_id=client_id, client_secret=client_secret) as downloader:
start = timer()
assert downloader.check_connection()
df = downloader.download(
tickers=tickers,
start_date=start_date,
show_progress=True,
metrics=["value", "eop_lag", "mop_lag", "grading"],
suppress_warning=True,
)
end = timer()
print("Download time from DQ: " + str(timedelta(seconds=end - start)))
dfd = df
Maximum number of tickers is 804
Downloading data from JPMaQS.
Timestamp UTC: 2025-04-10 12:48:36
Connection successful!
Requesting data: 100%|██████████| 161/161 [00:36<00:00, 4.45it/s]
Downloading data: 100%|██████████| 161/161 [01:00<00:00, 2.67it/s]
Some expressions are missing from the downloaded data. Check logger output for complete list.
1136 out of 3216 expressions are missing. To download the catalogue of all available expressions and filter the unavailable expressions, set `get_catalogue=True` in the call to `JPMaQSDownload.download()`.
Download time from DQ: 0:01:46.095299
Availability #
cids_exp = cids_dm + cids_em # cids expected in category panels
msm.missing_in_df(df, xcats=main, cids=cids_exp)
No missing XCATs across DataFrame.
Missing cids for CBCSCORE_SA_3MMA_ARMAS: ['AUD', 'COP', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RUB', 'SGD', 'THB', 'ZAR']
Missing cids for CBCSCORE_SA_3MMA_D1M1ML12_ARMAS: ['AUD', 'COP', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RUB', 'SGD', 'THB', 'ZAR']
Missing cids for CBCSCORE_SA_ARMAS: ['AUD', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'NOK', 'NZD', 'PEN', 'PLN', 'SGD']
Missing cids for CBCSCORE_SA_D1M1ML12_ARMAS: ['AUD', 'COP', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RUB', 'SGD', 'THB', 'ZAR']
Missing cids for CBCSCORE_SA_D1M1ML1_ARMAS: ['AUD', 'COP', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RUB', 'SGD', 'THB', 'ZAR']
Missing cids for CBCSCORE_SA_D1Q1QL1_ARMAS: ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'CZK', 'DEM', 'ESP', 'EUR', 'FRF', 'GBP', 'HKD', 'HUF', 'IDR', 'ILS', 'INR', 'ITL', 'JPY', 'KRW', 'MXN', 'NLG', 'NOK', 'NZD', 'PEN', 'PLN', 'RON', 'SEK', 'SGD', 'TRY', 'TWD', 'USD']
Missing cids for CBCSCORE_SA_D1Q1QL4_ARMAS: ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'CZK', 'DEM', 'ESP', 'EUR', 'FRF', 'GBP', 'HKD', 'HUF', 'IDR', 'ILS', 'INR', 'ITL', 'JPY', 'KRW', 'MXN', 'NLG', 'NOK', 'NZD', 'PEN', 'PLN', 'RON', 'SEK', 'SGD', 'TRY', 'TWD', 'USD']
Missing cids for CBCSCORE_SA_D2Q2QL2_ARMAS: ['AUD', 'BRL', 'CAD', 'CHF', 'CLP', 'CNY', 'CZK', 'DEM', 'ESP', 'EUR', 'FRF', 'GBP', 'HKD', 'HUF', 'IDR', 'ILS', 'INR', 'ITL', 'JPY', 'KRW', 'MXN', 'NLG', 'NOK', 'NZD', 'PEN', 'PLN', 'RON', 'SEK', 'SGD', 'TRY', 'TWD', 'USD']
Missing cids for CBCSCORE_SA_D3M3ML3_ARMAS: ['AUD', 'COP', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RUB', 'SGD', 'THB', 'ZAR']
Missing cids for CBCSCORE_SA_D6M6ML6_ARMAS: ['AUD', 'COP', 'GBP', 'HKD', 'IDR', 'INR', 'MXN', 'MYR', 'NOK', 'NZD', 'PEN', 'PHP', 'PLN', 'RUB', 'SGD', 'THB', 'ZAR']
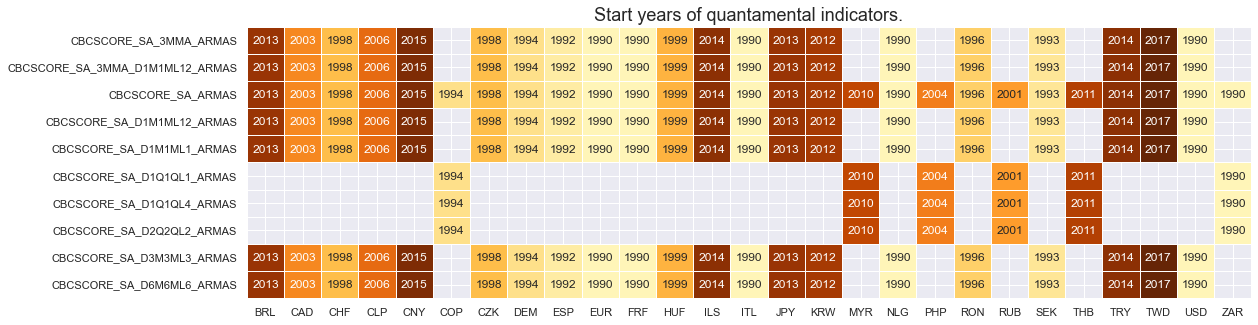
For most countries quantamental information states of construction output are available from the late 1990’s to early 2000’s with the late starters being Great Britain (2011), Indonesia (2011) and Malaysia (2016).
xcatx = cstr_conf
cidx = cids_exp
msm.check_availability(
df,
xcats=xcatx,
cids=cidx,
missing_recent=False,
)
print("Last updated:", date.today())
Last updated: 2025-04-10
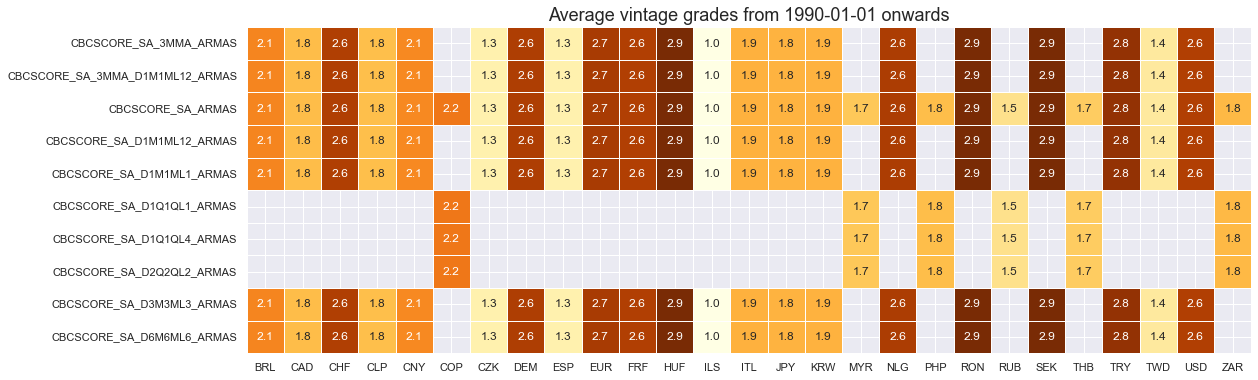
Quantamental information states of construction confidence are available for fewer currency areas than construction output (27 versus 30) and have a wide range of start dates from 1990 to 2021.
Vintage quality is mixed and at the limit for many emerging countries, as vintage information in electronic format is scarce.
xcatx = cstr_conf
cidx = cids_exp
plot = msp.heatmap_grades(
df,
xcats=xcatx,
cids=cidx,
size=(18, 6),
title=f"Average vintage grades from {start_date} onwards",
)
For graphical representation below, it is helpful to rename some quarterly dynamics into an equivalent monthly dynamics.
dict_repl = {
# Surprises ARMA(1,1) (ARMAS)
"CBCSCORE_SA_D1Q1QL1_ARMAS": "CBCSCORE_SA_D3M3ML3_ARMAS",
"CBCSCORE_SA_D2Q2QL2_ARMAS": "CBCSCORE_SA_D6M6ML6_ARMAS",
"CBCSCORE_SA_D1Q1QL4_ARMAS": "CBCSCORE_SA_3MMA_D1M1ML12-ARMAS",
}
for key, value in dict_repl.items():
dfd["xcat"] = dfd["xcat"].str.replace(key, value)
History #
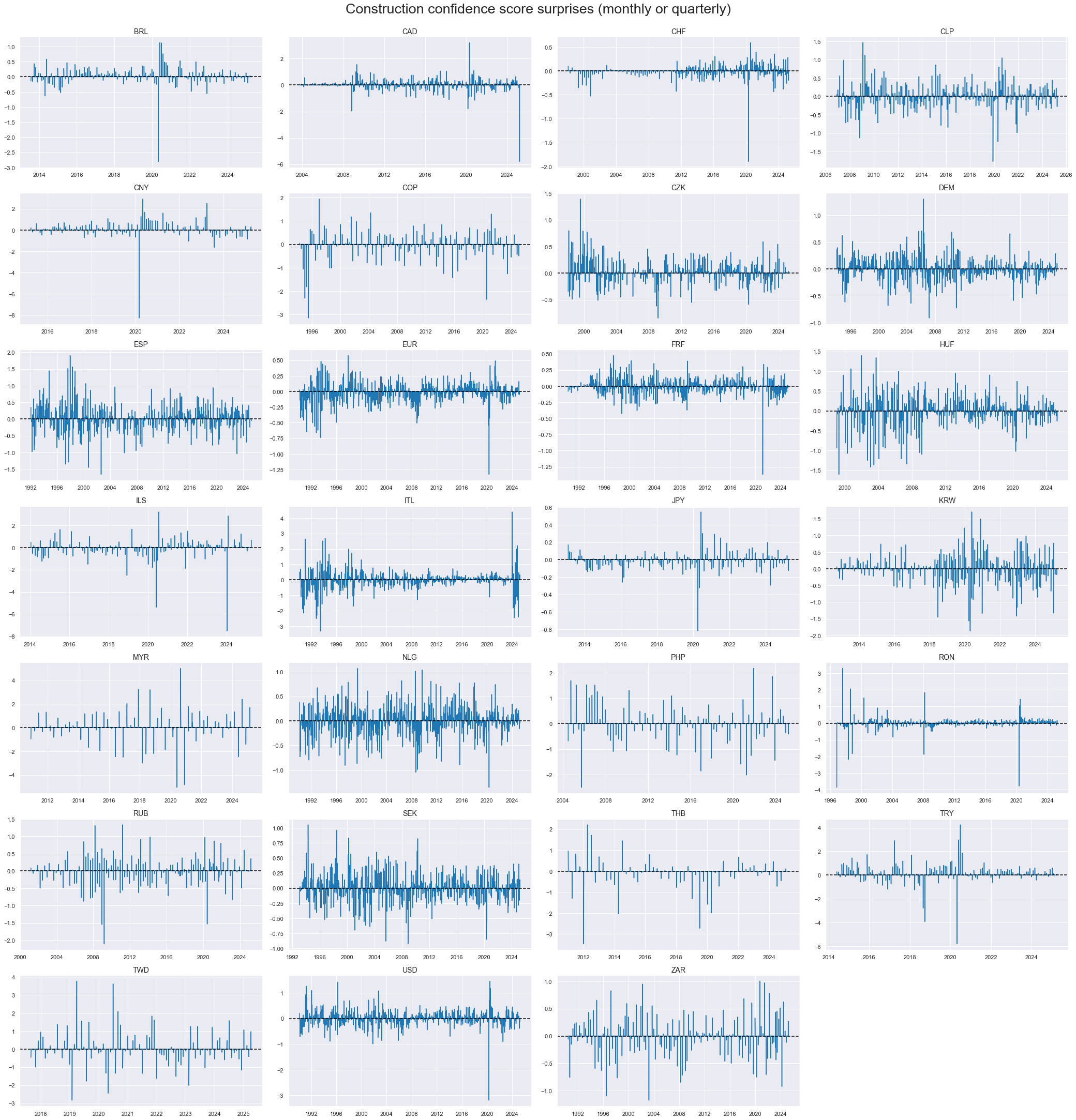
Construction survey score surprises #
cidx = cids
xcatx = ["CBCSCORE_SA_ARMAS"]
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start=start_date,
title="Construction confidence score surprises (monthly or quarterly)",
ncol=4,
same_y=False,
legend_fontsize=17,
title_fontsize=27,
size=(12, 7),
aspect=1.7,
all_xticks=True,
legend_ncol=2,
label_adj=0.05,
)
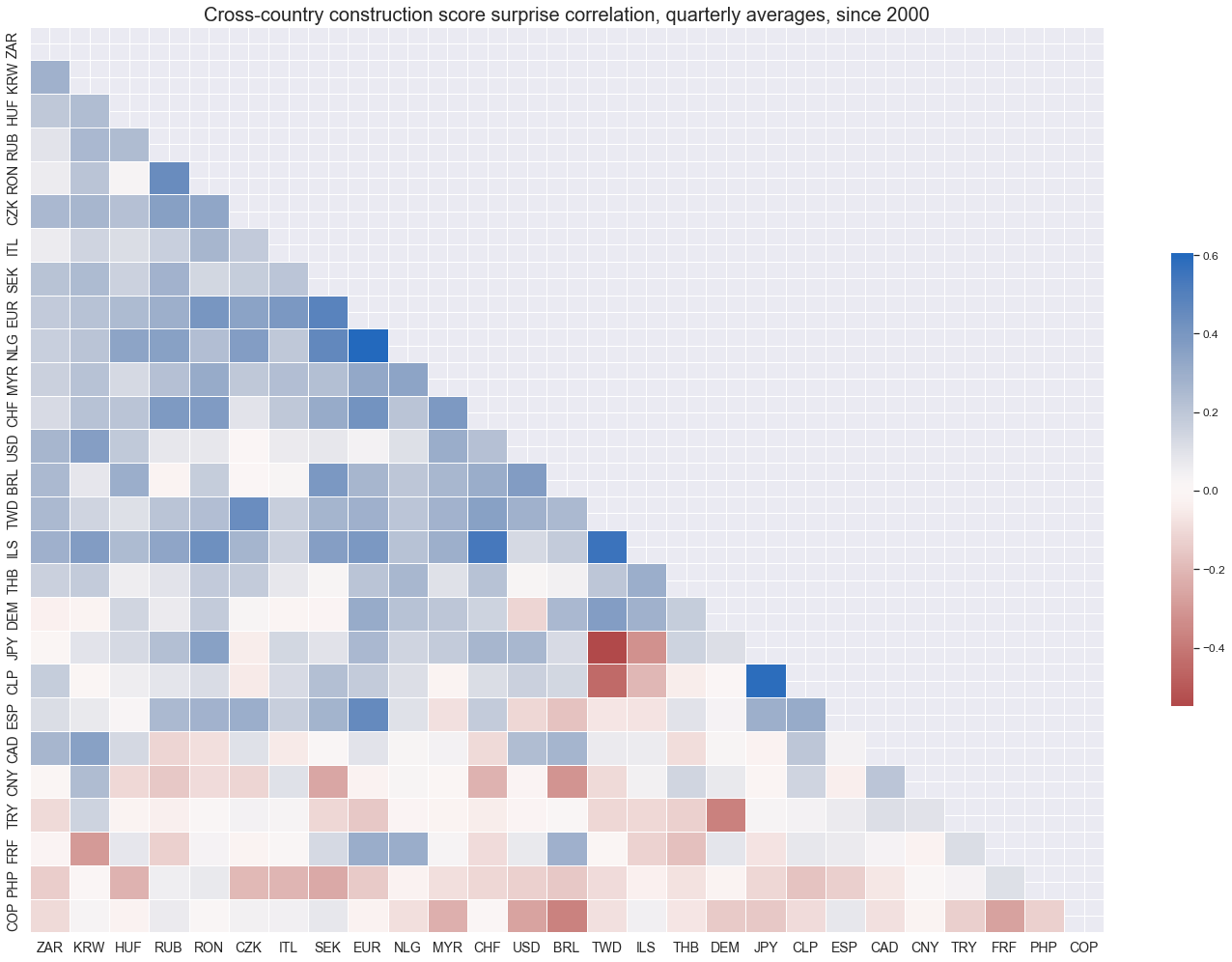
Construction survey score surprises are not generally positively correlated, even if aggregated over quarters.
cidx = cids
msp.correl_matrix(
dfd,
xcats="CBCSCORE_SA_ARMAS",
cids=cidx,
freq="q",
title="Cross-country construction score surprise correlation, quarterly averages, since 2000",
cluster=True,
size=(20, 14),
)
xcatx = ["CBCSCORE_SA_D3M3ML3_ARMAS", "CBCSCORE_SA_D6M6ML6_ARMAS"]
cidx = cids
msp.view_timelines(
dfd,
xcats=xcatx,
cids=cidx,
start=start_date,
title="Construction confidence change score surprises",
legend_fontsize=17,
title_fontsize=27,
ncol=4,
same_y=False,
size=(12, 7),
aspect=1.7,
all_xticks=True,
)
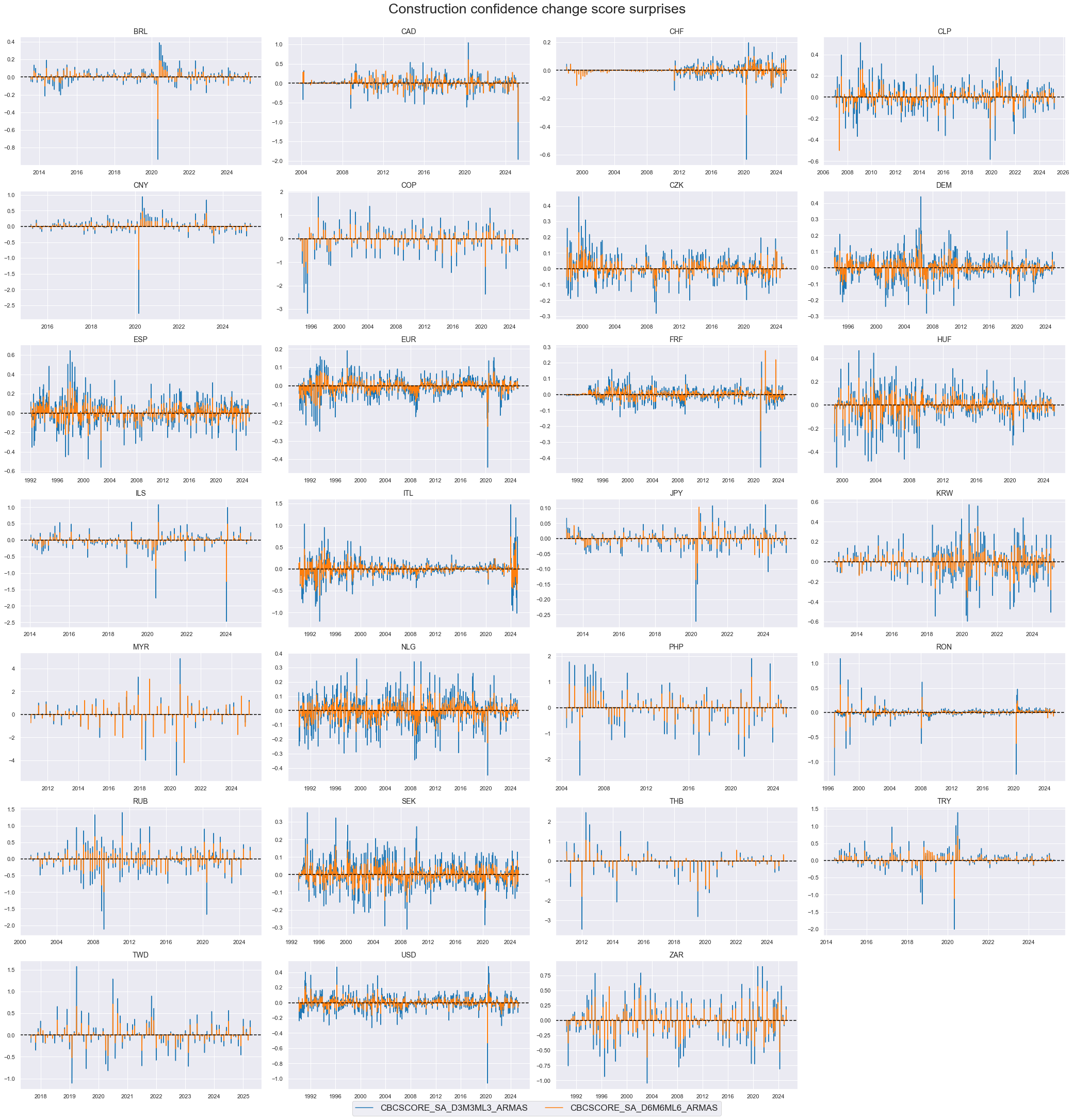
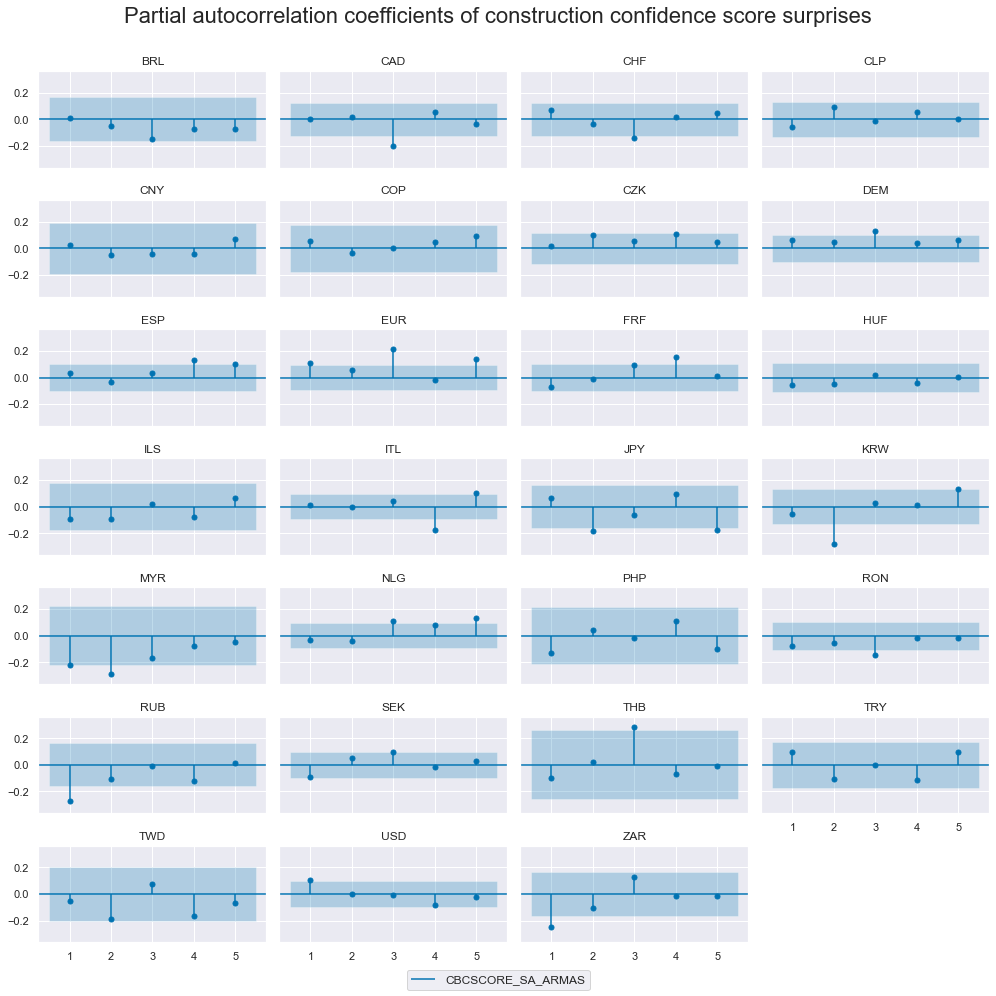
The autocorrelation (ACF) and partial autocorrelation (PACF) plots evaluate the temporal dependence of quantamental surprises across information events. Under the assumption of a well-specified prediction model of first-print releases and unbiased subsequent revisions, these surprises — interpreted as one-step-ahead forecast errors — should be serially uncorrelated.
msv.plot_pacf(
df=dfd,
cids=cidx,
xcat="CBCSCORE_SA_ARMAS",
title="Partial autocorrelation coefficients of construction confidence score surprises",
lags=5,
remove_zero_predictor=True,
figsize=(14, 14),
ncols=4,
)
Importance #
Research links #
On the link to metals markets: “The four most common metals used in construction are steel, aluminium, iron and copper. Each is used for its individual properties and the benefits that can be applied when constructing a building…Possibly the most widespread metal used within the industry, steel has many desirable attributes to assist with construction. One feature of steel is its availability; due to being 100% recyclable, the metal can be reused in endless amounts without losing any properties, making it one of the most sustainable metals in the industry… Aluminium is very lightweight, but also exceptionally durable, which are ideal properties for a building material that requires fast completion…Metal buildings, such as modern hospitals, high rises, offices and warehouses, are rarely built without aluminium…. Copper is a metal highly resistant to corrosion and has been used for centuries for construction. Alone, its strength is incomparable as even in colder climates, the material doesn’t crack, making it ideal for buildings in colder climates.” Morecamb metals
Empirical clues #
Construction information states as predictor for metals markets #
# Create global GDP-weighted construction activity and survey scores
xcatx = [
"CBCSCORE_SA_D3M3ML3_ARMAS",
"CBCSCORE_SA_3MMA_ARMAS",
]
for xc in xcatx:
dfa = msp.linear_composite(
df=dfd,
xcats=xc,
cids=cids,
weights="IVAWGT_SA_1YMA",
new_cid="GLB",
complete_cids=False,
)
dfd = msm.update_df(dfd, dfa)
# Calculate returns of construction-related metals basket
contracts = [c + "_CO" for c in cids_co]
bask_co = msp.Basket(df=dfd, contracts=contracts, ret="XR_NSA")
bask_co.make_basket(weight_meth="equal", basket_name="GLB_MTL")
dfa = bask_co.return_basket()
dfd = msm.update_df(dfd, dfa)
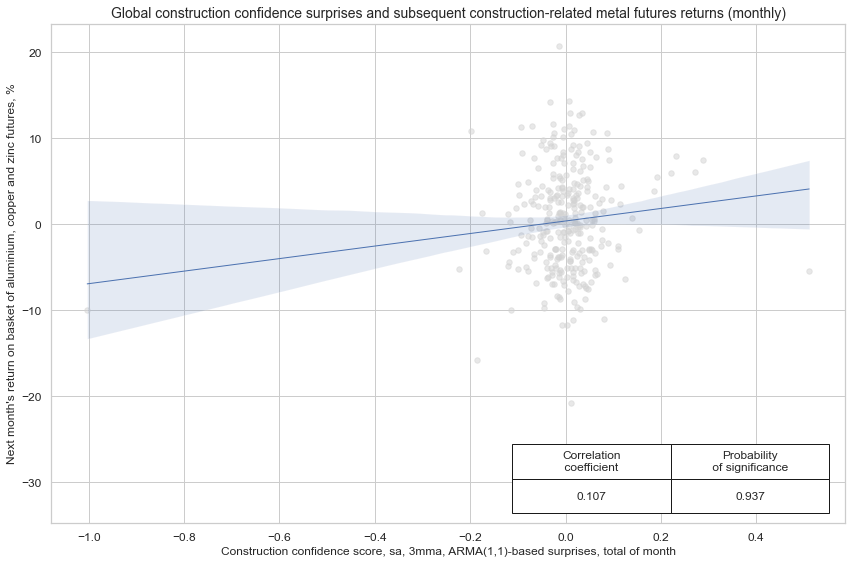
Construction confidence score surprises have positively predicted subsequent futures returns of metals that are associated with construction.
cr = msp.CategoryRelations(
dfd,
xcats=["CBCSCORE_SA_3MMA_ARMAS", "MTL_XR_NSA"],
cids=["GLB"],
freq="M",
lag=1,
xcat_aggs=["sum", "sum"],
fwin=1,
start="2000-01-01",
years=None,
)
cr.reg_scatter(
title="Global construction confidence surprises and subsequent construction-related metal futures returns (monthly)",
labels=False,
coef_box="lower right",
xlab="Construction confidence score, sa, 3mma, ARMA(1,1)-based surprises, total of month",
ylab="Next month's return on basket of aluminium, copper and zinc futures, %",
prob_est="pool",
remove_zero_predictor=True,
)
Appendices #
Appendix 1: Currency symbols #
The word ‘cross-section’ refers to currencies, currency areas or economic areas. In alphabetical order, these are AUD (Australian dollar), BRL (Brazilian real), CAD (Canadian dollar), CHF (Swiss franc), CLP (Chilean peso), CNY (Chinese yuan renminbi), COP (Colombian peso), CZK (Czech Republic koruna), DEM (German mark), ESP (Spanish peseta), EUR (Euro), FRF (French franc), GBP (British pound), HKD (Hong Kong dollar), HUF (Hungarian forint), IDR (Indonesian rupiah), ITL (Italian lira), JPY (Japanese yen), KRW (Korean won), MXN (Mexican peso), MYR (Malaysian ringgit), NLG (Dutch guilder), NOK (Norwegian krone), NZD (New Zealand dollar), PEN (Peruvian sol), PHP (Phillipine peso), PLN (Polish zloty), RON (Romanian leu), RUB (Russian ruble), SEK (Swedish krona), SGD (Singaporean dollar), THB (Thai baht), TRY (Turkish lira), TWD (Taiwanese dollar), USD (U.S. dollar), ZAR (South African rand).
Appendix 2: Quantamental economic surprises #
Quantamental economic surprises are defined as deviations of point-in-time quantamental indicators from expected values. Expected values are estimated predictions of an informed market participant. Following this definition there are two types of surprises that jointly make up economic surprise indicators:
• A first print event is the difference between a quantamental indicator on a release date and its expected value. A release date is the day on which any underlying economic time series adds an observation period. Expected values are estimated, typically based on econometric models and information prior to the release date. A quantamental data surprise is always specific to the prediction model or statistical learning process.
• A pure revision event is the change in a quantamental indicator on a non-release date. It arises from revisions of data for previously released observation periods. Per default, it is assumed that all revisions are surprises, i.e., that the latest reported value for an observation period is the best predictor its value after revisions. Note that any revisions published on a release date become part of the first print event.
A quantamental indicator of economic surprises records the values of these two events on the dates they become known. It records zero values for all other dates. Models for predicting indicator values always use the latest vintage of the underlying data series. They are typically applied to increments, i.e., differences or log differences of volume, value or price indices. The predicted next increment produces an expected new vintage, and the expected new vintage implies a new derived expected quantamental indicator, such as an annual growth rate or moving average. Note than in this way predictions automatically account for “base effects”, i.e., predictable changes in growth rates that arise from unusually sharp increase of declines in index levels of the base period, for example a year ago.